IB

Math SL1: Trig Practice Problems

Alei - Desert Academy
Circular Functions and Trig - Practice Problems (to 07)
1.

In the triangle PQR, PR = 5 cm, QR = 4 cm and PQ = 6 cm.

Calculate
(a)
(b)

the size of
;
the area of triangle PQR.
(Total 6 marks)

2.

3.

The following diagram shows a triangle ABC, where

(a)

Show that sin =

(b)

Show that sin 2 =

(c)

Find the exact value of cos 2.

is 90, AB = 3, AC = 2 and

is .

.
.

(Total 6 marks)
The following diagram shows a sector of a circle of radius r cm, and angle at the centre. The perimeter of the
sector is 20 cm.

(a)

Show that =

(b)

2
The area of the sector is 25 cm . Find the value of r.

(Total 6 marks)
4.

The following diagram shows the triangle AOP, where OP = 2 cm, AP = 4 cm and AO = 3 cm.

(a)

Calculate

, giving your answer in radians.

(3)

The following diagram shows two circles which intersect at the points A and B. The smaller circle C1 has centre
O and radius 3 cm, the larger circle C2 has centre P and radius 4 cm, and OP = 2 cm. The point D lies on the
circumference of C1 and E on the circumference of C2.Triangle AOP is the same as triangle AOP in the diagram
above.

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 1 of 23

IB Math SL1: Trig Practice Problems

Alei - Desert Academy

(b)

Find

, giving your answer in radians.

(c)

Given that
is 1.63 radians, calculate the area of
(i)
sector PAEB;
(ii)
sector OADB.

(2)

(5)
(d)

The area of the quadrilateral AOBP is 5.81 cm .

(i)
Find the area of AOBE.
(ii)
Hence find the area of the shaded region AEBD.
(4)
(Total 14 marks)

5.

The following diagram shows a pentagon ABCDE, with AB = 9.2 cm, BC = 3.2 cm, BD = 7.1 cm,
= 52 and

(a)

Find AD.

(b)

Find DE.

=110,

= 60.

(4)
(4)
2

(c)

The area of triangle BCD is 5.68 cm . Find

(d)

Find AC.

(e)

Find the area of quadrilateral ABCD.

.
(4)
(4)
(5)
(Total 21 marks)

6.

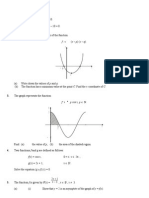
The diagram below shows the graph of f (x) = 1 + tan

(a)

for 360 x 360.

On the same diagram, draw the asymptotes.

(2)

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 2 of 23

IB Math SL1: Trig Practice Problems

(b)

Write down
(i)
the period of the function;
(ii)
the value of f (90).

(c)

Solve f (x) = 0 for 360 x 360.

Alei - Desert Academy

(2)
(2)
(Total 6 marks)
7.

(a)

2
Consider the equation 4x + kx + 1 = 0. For what values of k does this equation have two equal roots?
(3)

Let f be the function f ( ) = 2 cos 2 + 4 cos + 3, for 360 360.

2
(b)
Show that this function may be written as f ( ) = 4 cos + 4 cos + 1.
(1)
(c)

Consider the equation f ( ) = 0, for 360 360.

(i)
How many distinct values of cos satisfy this equation?
(ii)
Find all values of which satisfy this equation.

(d)

Given that f ( ) = c is satisfied by only three values of , find the value of c.

(5)

8.

(2)
(Total 11 marks)
A Ferris wheel with centre O and a radius of 15 metres is represented in the diagram below. Initially seat A is at
ground level. The next seat is B, where

(a)

Find the length of the arc AB.

(b)

Find the area of the sector AOB.

(2)
(2)
(c)

The wheel turns clockwise through an angle of

. Find the height of A above the ground.

(3)

The height, h metres, of seat C above the ground after t minutes, can be modelled by the function
h (t) = 15 15 cos
.
(d)

(i)

Find the height of seat C when t =

(ii)
(iii)

Find the initial height of seat C.

Find the time at which seat C first reaches its highest point.
(8)

(e)

Find h (t).

(f)

For 0 t ,
(i)
sketch the graph of h;
(ii)
find the time at which the height is changing most rapidly.

(2)

(5)
(Total 22 marks)
9.

2
Let f (x) = a (x 4) + 8.
(a)
Write down the coordinates of the vertex of the curve of f.
(b)
Given that f (7) = 10, find the value of a.
(c)
Hence find the y-intercept of the curve of f.
(Total 6 marks)

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 3 of 23

IB Math SL1: Trig Practice Problems

10.

Alei - Desert Academy

The following diagram shows a circle with radius r and centre O. The points A, B and C are on the circle and
=.

The area of sector OABC is

and the length of arc ABC is

Find the value of r and of .

(Total 6 marks)
11.

Let (x) = a sin b (x c). Part of the graph of is given below.

Given that a, b and c are positive, find the value of a, of b and of c.

(Total 6 marks)
12.

The points P(2, 4), Q (3, 1) and R (1, 6) are shown in the diagram below.

(a)
(b)

Find the vector

.
Find a vector equation for the line through R parallel to the line (PQ).
(Total 6 marks)

13.

The diagram below shows a circle of radius r and centre O. The angle

= .

2
The length of the arc AB is 24 cm. The area of the sector OAB is 180 cm .
Find the value of r and of .
(Total 6 marks)
14.

The diagram below shows a quadrilateral ABCD. AB = 4, AD = 8, CD =12, B

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

D = 25,

=.

Page 4 of 23

IB Math SL1: Trig Practice Problems

(a)

Alei - Desert Academy

Use the cosine rule to show that BD =

.
(2)

Let = 40.
(b)

(i)

Find the value of sin

(ii)

Find the two possible values for the size of

(iii)

Given that

is an acute angle, find the perimeter of ABCD.

(12)

(c)

Find the area of triangle ABD.

(2)
(Total 16 marks)

15.

2
Let y = 16x + 160x 256. Given that y has a maximum value, find
(i)
the value of x giving the maximum value of y;
(ii)
this maximum value of y.
The triangle XYZ has XZ = 6, YZ = x, XY = z as shown below. The perimeter of triangle XYZ is 16.
(a)

(4)

(b)

(i)

Express z in terms of x.

(ii)

2
Using the cosine rule, express z in terms of x and cos Z.

(iii)

Hence, show that cos Z =

.
(7)

Let the area of triangle XYZ be A.

2
2 2
(c)
Show that A = 9x sin Z.
(2)
2

(d)

Hence, show that A = 16x + 160x 256.

(e)

(i)
(ii)

(4)
Hence, write down the maximum area for triangle XYZ.
What type of triangle is the triangle with maximum area?
(3)
(Total 20 marks)
16.

The function f is defined by f : x 30 sin 3x cos 3x, 0 x

(a)
(b)

17.

Write down an expression for f (x) in the form a sin 6x, where a is an integer.
Solve f (x) = 0, giving your answers in terms of .

(Total 6 marks)
The following diagram shows two semi-circles. The larger one has centre O and radius 4 cm. The smaller one has
centre P, radius 3 cm, and passes through O. The line (OP) meets the larger semi-circle at S. The semi-circles
intersect at Q.

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 5 of 23

IB Math SL1: Trig Practice Problems

(a)

Alei - Desert Academy

(i)

Explain why OPQ is an isosceles triangle.

(ii)

Use the cosine rule to show that cos

(iii)

Hence show that sin

(iv)

Find the area of the triangle OPQ.

.
(7)

(b)

Consider the smaller semi-circle, with centre P.

(i)
(ii)

Write down the size of

Calculate the area of the sector OPQ.
(3)

(c)

Consider the larger semi-circle, with centre O. Calculate the area of the sector QOS.

(d)

Hence calculate the area of the shaded region.

(3)
(4)
(Total 17 marks)
18.

The graph of a function of the form y = p cos qx is given in the diagram below.

(a)
(b)
19.

Write down the value of p.

Calculate the value of q.

(Total 6 marks)
A farmer owns a triangular field ABC. One side of the triangle, [AC], is 104 m, a second side, [AB], is 65 m and
the angle between these two sides is 60.
(a)
Use the cosine rule to calculate the length of the third side of the field.
(3)
(b)

Given that sin 60 =

find the area of the field in the form

where p is an integer.
(3)

Let D be a point on [BC] such that [AD] bisects the 60 angle. The farmer divides the field into two parts A1 and
A2 by constructing a straight fence [AD] of length x metres, as shown on the diagram below.

(c)

(i)

Show that the area of Al is given by

(ii)

Find a similar expression for the area of A2.

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 6 of 23

IB Math SL1: Trig Practice Problems

(iii)

Alei - Desert Academy

Hence, find the value of x in the form

, where q is an integer.
(7)

(d)

(i)
(ii)

Explain why
.
Use the result of part (i) and the sine rule to show that
.

20.

(5)
(Total 18 marks)
2
The following diagram shows a circle of centre O, and radius r. The shaded sector OACB has an area of 27 cm .
Angle

= = 1.5 radians.

(a)
Find the radius.
(b)
Calculate the length of the minor arc ACB.
Working:
Answers:
(a) ..................................................................
(b) ..................................................................
(Total 6 marks)
21.

Consider y = sin

(a)

The graph of y intersects the x-axis at point A. Find the x-coordinate of A, where 0 x .

(b)

Solve the equation sin

, for 0 x 2.

Working:
Answers:
(a) ..................................................................
(b) ..................................................................
22.

(Total 6 marks)
The diagram shows a triangular region formed by a hedge [AB], a part of a river bank [AC] and a fence [BC]. The
hedge is 17 m long and
is 29. The end of the fence, point C, can be positioned anywhere along the river
bank.
(a)
Given that point C is 15 m from A, find the length of the fence [BC].

(3)
(b)

The farmer has another, longer fence. It is possible for him to enclose two different triangular regions with
this fence. He places the fence so that
is 85.
(i)
Find the distance from A to C.
(ii)
Find the area of the region ABC with the fence in this position.
(5)

(c)

To form the second region, he moves the fencing so that point C is closer to point A.
Find the new distance from A to C.

(d)

Find the minimum length of fence [BC] needed to enclose a triangular region ABC.

(4)
Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 7 of 23

IB Math SL1: Trig Practice Problems

Alei - Desert Academy

(2)
(Total 14 marks)

23.

Let f (x) =

sin 2x + cos x for 0 x 2.

(a)

Find f (x).

(i)

2
One way of writing f (x) is 2 sin x sin x + 1.
2
(ii)
Factorize 2 sin x + sin x 1.
(iii) Hence or otherwise, solve f (x) = 0.
(6)
The graph of y = f (x) is shown below.

There is a maximum point at A and a minimum point at B.

(b)
Write down the x-coordinate of point A.
(1)
(c)

The region bounded by the graph, the x-axis and the lines x = a and x = b is shaded in the diagram above.
(i)
Write down an expression that represents the area of this shaded region.
(ii)
Calculate the area of this shaded region.
(5)
(Total 12 marks)

24.

2
In triangle PQR, PQ is 10 cm, QR is 8 cm and angle PQR is acute. The area of the triangle is 20 cm . Find the
size of angle
(Total 6 marks)

25.

Let f (x) = 6 sin x , and g (x) = 6e

maximum value at B (0.5, b).

(a)
(b)
(c)

3 , for 0 x 2. The graph of f is shown on the diagram below. There is a

Write down the value of b.

On the same diagram, sketch the graph of g.
Solve f (x) = g (x) , 0.5 x 1.5.
(Total 6 marks)

26.

Consider the equation 3 cos 2x + sin x = 1

(a)
(b)
(c)

27.

2
Write this equation in the form f (x) = 0 , where f (x) = p sin x + q sin x + r , and p , q , r
Factorize f (x).
Write down the number of solutions of f (x) = 0, for 0 x 2.

(Total 6 marks)
The diagram below shows two circles which have the same centre O and radii 16 cm and 10 cm respectively. The
two arcs AB and CD have the same sector angle = 1.5 radians.

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 8 of 23

IB Math SL1: Trig Practice Problems

28.

Alei - Desert Academy

Find the area of the shaded region.

Let f (x) = sin (2x + 1), 0 x .
(a)
Sketch the curve of y = f (x) on the grid below.

(Total 6 marks)

(b)

29.

Find the x-coordinates of the maximum and minimum points of f (x), giving your answers correct to one
decimal place.
(Total 6 marks)
2
In a triangle ABC, AB = 4 cm, AC = 3 cm and the area of the triangle is 4.5 cm .
Find the two possible values of the angle
Working:

.
Answer:
..
(Total 6 marks)

30.

Solve the equation 2 cos x = sin 2x for 0 x , giving your answers in terms of .
Working:
Answer:
..
(Total 6 marks)

31.

The depth y metres of water in a harbour is given by the equation

y = 10 + 4 sin

where t is the number of hours after midnight.

(a)
Calculate the depth of the water
(i)
when t = 2;
(ii)
at 2100.
(3)
The sketch below shows the depth y, of water, at time t, during one day (24 hours).

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 9 of 23

IB Math SL1: Trig Practice Problems

(b)

(i)
(ii)

Alei - Desert Academy

Write down the maximum depth of water in the harbour.

Calculate the value of t when the water is first at its maximum depth during the day.
(3)

The harbour gates are closed when the depth of the water is less than seven metres. An alarm rings when the gates
are opened or closed.
(c)
(i)
How many times does the alarm sound during the day?
(ii)
Find the value of t when the alarm sounds first.
(iii) Use the graph to find the length of time during the day when the harbour gates are closed. Give
your answer in hours, to the nearest hour.
(7)
(Total 13 marks)
32.

The following diagram shows a triangle ABC, where BC = 5 cm,

= 60,

= 40.

(a)
Calculate AB.
(b)
Find the area of the triangle.
Working:
Answers:
(a) ..
(b) ..
(Total 6 marks)
33.

The diagram below shows a circle of radius 5 cm with centre O. Points A and B are on the circle, and
0.8 radians. The point N is on [OB] such that [AN] is perpendicular to [OB].

is

Find the area of the shaded region.

Working:
Answer:
........
(Total 6 marks)
Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 10 of 23

IB Math SL1: Trig Practice Problems

34.

Alei - Desert Academy

Let f (x) = 1 + 3 cos (2x) for 0 x , and x is in radians.

(a)
(i)
Find f (x).
(ii)
Find the values for x for which f (x) = 0, giving your answers in terms of .
(6)
The function g (x) is defined as g (x) = f (2x) 1, 0 x
(b)

35.

(i)

The graph of f may be transformed to the graph of g by a stretch in the x-direction with scale factor
followed by another transformation. Describe fully this other transformation.

(ii)

Find the solution to the equation g (x) = f (x)

(4)
(Total 10 marks)
Part of the graph of y = p + q cos x is shown below. The graph passes through the points (0, 3) and (, 1).

Find the value of

(a)
p;
(b)
q.
Working:
Answers:
(a) ..................................................................
(b) ..................................................................
(Total 6 marks)
36.

37.

Find all solutions of the equation cos 3x = cos (0.5x), for 0 x .

Working:
Answer:
..................................................................
(Total 6 marks)
The diagram below shows a triangle and two arcs of circles.
The triangle ABC is a right-angled isosceles triangle, with AB = AC = 2. The point P is the midpoint of [BC].
The arc BDC is part of a circle with centre A.
The arc BEC is part of a circle with centre P.

(a)
(b)

Calculate the area of the segment BDCP.

Calculate the area of the shaded region BECD.
(Total 6 marks)

38.

The diagram shows a parallelogram OPQR in which

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 11 of 23

IB Math SL1: Trig Practice Problems

(a)

Find the vector

Alei - Desert Academy

.
(3)

(b)

Use the scalar product of two vectors to show that cos

=
(4)

(c)

39.

(i)

Explain why cos

= cos

(ii)

Hence show that sin

(iii)

Calculate the area of the parallelogram OPQR, giving your answer as an integer.

(7)
(Total 14 marks)
The points P, Q, R are three markers on level ground, joined by straight paths PQ, QR, PR as shown in the
diagram. QR = 9 km,

= 35,

= 25.
Diagram not to scale

(a)

Find the length PR.

(3)
1

(b)

Tom sets out to walk from Q to P at a steady speed of 8 km h . At the same time, Alan sets out to jog
1
from R to P at a steady speed of a km h . They reach P at the same time. Calculate the value of a.

(c)

The point S is on [PQ], such that RS = 2QS, as shown in the diagram.

(7)

Find the length QS.

(6)
(Total 16 marks)
40.

Consider the function f (x) = cos x + sin x.

(a)

(i)

Show that f (

) = 0.

(ii)

Find in terms of , the smallest positive value of x which satisfies f (x) = 0.

(3)
x

The diagram shows the graph of y = e (cos x + sin x), 2 x 3. The graph has a maximum turning point at C(a,
b) and a point of inflexion at D.

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 12 of 23

IB Math SL1: Trig Practice Problems

(b)

Find

(c)

Find the exact value of a and of b.

Alei - Desert Academy

.
(3)
(4)

(d)

Show that at D, y =

(e)

Find the area of the shaded region.

(5)
(2)
(Total 17 marks)
41.

The graph of the function f (x) = 3x 4 intersects the x-axis at A and the y-axis at B.
(a)
Find the coordinates of
(i)
A;
(ii)
B.
(b)
Let O denote the origin. Find the area of triangle OAB.
Working:
Answers:
(a) (i) ...........................................................
(ii) ...........................................................
(b) ..................................................................
(Total 6 marks)
2

42.

(a)

Factorize the expression 3 sin x 11 sin x + 6.

2
(b)
Consider the equation 3 sin x 11 sin x + 6 = 0.
(i)
Find the two values of sin x which satisfy this equation,
(ii)
Solve the equation, for 0 x 180.
Working:
Answers:
(a) ..................................................................
(b) (i) ...........................................................
(ii) ...........................................................

43.

(Total 6 marks)
The diagram below shows a circle, centre O, with a radius 12 cm. The chord AB subtends at an angle of 75 at the
centre. The tangents to the circle at A and at B meet at P.

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 13 of 23

IB Math SL1: Trig Practice Problems

(a)

Using the cosine rule, show that the length of AB is 12

(b)

Find the length of BP.

(c)

Hence find
(i)
the area of triangle OBP;
(ii)
the area of triangle ABP.

(d)

Find the area of sector OAB.

(e)

Find the area of the shaded region.

Alei - Desert Academy

.
(2)
(3)

(4)
(2)
(2)
(Total 13 marks)
44.

Note: Radians are used throughout this question.

A mass is suspended from the ceiling on a spring. It is pulled down to point P and then released. It oscillates up
and down.

Its distance, s cm, from the ceiling, is modelled by the function s = 48 + 10 cos 2t where t is the time in seconds
from release.
(a)
(i)
What is the distance of the point P from the ceiling?
(ii)
How long is it until the mass is next at P?
(5)
(b)

(i)

Find

(ii)

Where is the mass when the velocity is zero?

(7)

A second mass is suspended on another spring. Its distance r cm from the ceiling is modelled by the function r =
60 + 15 cos 4t. The two masses are released at the same instant.
(c)
Find the value of t when they are first at the same distance below the ceiling.
(2)
(d)

In the first three seconds, how many times are the two masses at the same height?
(2)
(Total 16 marks)

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 14 of 23

IB Math SL1: Trig Practice Problems

45.

Alei - Desert Academy

The following diagram shows a circle of centre O, and radius 15 cm. The arc ACB subtends an angle of 2 radians
at the centre O.

Find
(a)
the length of the arc ACB;
(b)
the area of the shaded region.
Working:
Answers:
(a) ..................................................................
(b) ..................................................................
(Total 6 marks)
46.

Two boats A and B start moving from the same point P. Boat A moves in a straight line at 20 km h
1
moves in a straight line at 32 km h . The angle between their paths is 70.
Find the distance between the boats after 2.5 hours.

47.

Let f (x) = sin 2x and g (x) = sin (0.5x).

(a)
Write down
(i)
the minimum value of the function f ;
(ii)
the period of the function g.
(b)
Consider the equation f (x) = g (x).

and boat B

(Total 6 marks)

Find the number of solutions to this equation, for 0 x

Working:
Answers:
(a) (i) ..........................................................
(ii) ..........................................................
(b) .................................................................
(Total 6 marks)
48.

Consider the following statements

x
A:
log10 (10 ) > 0.
B:
0.5 cos (0.5x) 0.5.
arctan x

C:

(a)

Determine which statements are true for all real numbers x. Write your answers (yes or no) in the table
below.
Statement
(a) Is the statement true for all
(b) If not true, example
real numbers x? (Yes/No)
A
B
C

(b)

If a statement is not true for all x, complete the last column by giving an example of one value of x for
which the statement is false.
Working:
(Total 6 marks)

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 15 of 23

IB Math SL1: Trig Practice Problems

49.

Alei - Desert Academy

The diagram shows a triangle ABC in which AC = 7

(a)

Use the fact that sin 45 =

, BC = 6,

to show that sin

= 45.

.
(2)

The point D is on (AB), between A and B, such that sin

(b)

(i)
(ii)
(iii)

Write down the value of

Calculate the angle BCD.
Find the length of [BD].

.
(6)

(c)

Show that

.
(2)
(Total 10 marks)

50.

In triangle ABC, AC = 5, BC = 7,

= 48, as shown in the diagram.

Find
giving your answer correct to the nearest degree.
Working:
Answer:
......................................................................
(Total 6 marks)
51.

Given that sin x =

, where x is an acute angle, find the exact value of

(a)
cos x;
(b)
cos 2x.
Working:
Answers:
(a) ..................................................................
(b) ..................................................................
(Total 6 marks)
52.

Consider the trigonometric equation 2 sin x = 1 + cos x.

2
Write this equation in the form f (x) = 0, where f (x) = a cos x + b cos x + c,
and a, b, c .
(b)
Factorize f (x).
(c)
Solve f (x) = 0 for 0 x 360.
Working:
Answers:
(a) ..................................................................
(a)

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 16 of 23

IB Math SL1: Trig Practice Problems

Alei - Desert Academy

(b)
(c)

..................................................................
..................................................................
(Total 6 marks)

53.

The following diagram shows a triangle with sides 5 cm, 7 cm, 8 cm.

Diagram not to scale

Find
(a)
the size of the smallest angle, in degrees;
(b)
the area of the triangle.
Working:
Answers:
(a) ..................................................................
(b) ..................................................................
(Total 4 marks)
2

54.

(a)
(b)

Write the expression 3 sin x + 4 cos x in the form a cos x + b cos x + c.

Hence or otherwise, solve the equation
2
3 sin x + 4 cos x 4 = 0,
0 x 90.
Working:
Answers:
(a) ..................................................................
(b) ..................................................................

55.

In the following diagram, O is the centre of the circle and (AT) is the tangent to the circle at T.

(Total 4 marks)

Diagram not to scale

If OA = 12 cm, and the circle has a radius of 6 cm, find the area of the shaded region.
Working:
Answer:
.......................................................................
(Total 4 marks)
56.

In the diagram below, the points O(0, 0) and A(8, 6) are fixed. The angle
varies as the point P(x, 10) moves along the horizontal line y = 10.

Diagram to scale
(a)

(i)

Show that

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 17 of 23

IB Math SL1: Trig Practice Problems

(ii)

Alei - Desert Academy

Write down a similar expression for OP in terms of x.

(2)

(b)

Hence, show that

(3)
(c)

Find, in degrees, the angle

when x = 8.
(2)

(d)

Find the positive value of x such that

.
(4)

Let the function f be defined by

(e)

57.

Consider the equation f (x) = 1.

(i)
Explain, in terms of the position of the points O, A, and P, why this
equation has a solution.
(ii)
Find the exact solution to the equation.

(5)
(Total 16 marks)
The diagram below shows a sector AOB of a circle of radius 15 cm and centre O. The angle at the centre of the
circle is 2 radians.
Diagram not to scale

(a)
Calculate the area of the sector AOB.
(b)
Calculate the area of the shaded region.
Working:
Answers:
(a) ..................................................................
(b) ..................................................................
(Total 4 marks)
58.

The diagrams below show two triangles both satisfying the conditions
AB = 20 cm, AC = 17 cm,
Diagrams not
to scale

= 50.

(a)
Calculate the size of
in Triangle 2.
(b)
Calculate the area of Triangle 1.
Working:
Answers:
(a) ..................................................................
Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 18 of 23

IB Math SL1: Trig Practice Problems

Alei - Desert Academy

(b)

..................................................................
(Total 4 marks)

59.

The depth, y metres, of sea water in a bay t hours after midnight may be represented by the function
, where a, b and k are constants.

60.

The water is at a maximum depth of 14.3 m at midnight and noon, and is at a minimum depth of 10.3 m at 06:00
and at 18:00.
Write down the value of
(a)
a;
(b)
b;
(c)
k.
Working:
Answers:
(a) ..................................................................
(b) ..................................................................
(c) ..................................................................
(Total 4 marks)
Town A is 48 km from town B and 32 km from town C as shown in the diagram.

Given that town B is 56 km from town C, find the size of angle

to the nearest degree.

(Total 4 marks)

61.

62.

(a)

Express 2 cos x + sin x in terms of sin x only.

2
(b)
Solve the equation 2 cos x + sin x = 2 for x in the interval 0 x , giving your answers exactly.
(Total 4 marks)
Note: Radians are used throughout this question.
(a)
Draw the graph of y = + x cos x, 0 x 5, on millimetre square graph paper, using a scale of 2 cm per
unit. Make clear
(i)
the integer values of x and y on each axis;
(ii)
the approximate positions of the x-intercepts and the turning points.
(5)
(b)
Without the use of a calculator, show that is a solution of the equation
+ x cos x = 0.
(3)
(c)
Find another solution of the equation + x cos x = 0 for 0 x 5, giving your answer to six significant
figures.
(2)
(d)
Let R be the region enclosed by the graph and the axes for 0 x . Shade R on your diagram, and write
down an integral which represents the area of R .
(2)
(e)
Evaluate the integral in part (d) to an accuracy of six significant figures. (If you consider it necessary, you
can make use of the result
(3)
(Total 15 marks)

63.

A formula for the depth d metres of water in a harbour at a time t hours after midnight is

where P and Q are positive constants. In the following graph the point (6, 8.2) is a minimum point and the point
Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 19 of 23

IB Math SL1: Trig Practice Problems

Alei - Desert Academy

(12, 14.6) is a maximum point.

(a)

Find the value of

(i)
Q;
(ii)
P.

(b)

Find the first time in the 24-hour period when the depth of the water is 10 metres.

(c)

(i)
(ii)

(3)
(3)
Use the symmetry of the graph to find the next time when the depth of the water is 10 metres.
Hence find the time intervals in the 24-hour period during which the water is less than 10 metres
deep.

64.

(4)
Solve the equation 3 cos x = 5 sin x, for x in the interval 0 x 360, giving your answers to the nearest degree.
(Total 4 marks)

65.

If A is an obtuse angle in a triangle and sin A =

66.

(a)

(b)

(c)

, calculate the exact value of sin 2A.

(Total 4 marks)
Sketch the graph of y = sin x x, 3 x 3, on millimetre square paper, using a scale of 2 cm per unit
on each axis.
Label and number both axes and indicate clearly the approximate positions of the
x-intercepts and the local maximum and minimum points.
(5)
Find the solution of the equation
sin x x = 0,
x > 0.
(1)
Find the indefinite integral
and hence, or otherwise, calculate the area of the region enclosed by the graph, the
x-axis and the line x = 1.
(4)
(Total 10 marks)

67.

Given that sin =

(a)
(b)

68.

, cos =

and 0 360,

find the value of ;

write down the exact value of tan .

(Total 4 marks)
The diagram shows a vertical pole PQ, which is supported by two wires fixed to the horizontal ground at A and B.

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 20 of 23

IB Math SL1: Trig Practice Problems

Alei - Desert Academy

= 40 m
= 36
= 70
= 30

Find
(a)
(b)

the height of the pole, PQ;

the distance between A and B.
(Total 4 marks)

69.

The diagram shows a circle of radius 5 cm.

Find the perimeter of the shaded region.

(Total 4 marks)
70.

f (x) = 4 sin

For what values of k will the equation f (x) = k have no solutions?

71.

(Total 4 marks)
In this question you should note that radians are used throughout.
2
(a)
(i)
Sketch the graph of y = x cos x, for 0 x 2 making clear the approximate positions of the
positive x-intercept, the maximum point and the end-points.
(ii)
Write down the approximate coordinates of the positive x-intercept, the maximum point and the
end-points.
(7)
(b)
Find the exact value of the positive x-intercept for 0 x 2.
(2)
Let R be the region in the first quadrant enclosed by the graph and the x-axis.
(c)
(i)
Shade R on your diagram.
(ii)
Write down an integral which represents the area of R.
(3)
(d)
Evaluate the integral in part (c)(ii), either by using a graphic display calculator, or by using the following
information.
2
2
(x sin x + 2x cos x 2 sin x) = x cos x.
(3)
(Total 15 marks)

72.

In this part of the question, radians are used throughout.

The function f is given by
2
f (x) = (sin x) cos x.
The following diagram shows part of the graph of y = f (x).

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 21 of 23

IB Math SL1: Trig Practice Problems

Alei - Desert Academy

The point A is a maximum point, the point B lies on the x-axis, and the point C is a point of inflexion.
(a)
Give the period of f.
(1)
(b)

From consideration of the graph of y = f (x), find to an accuracy of one significant figure the range of f.

(c)

(i)

Find f (x).

(ii)

Hence show that at the point A, cos x =

(iii)

Find the exact maximum value.

(1)
.
(9)
(d)

Find the exact value of the x-coordinate at the point B.

(1)

(e)

(i)

Find

dx.

(ii)

Find the area of the shaded region in the diagram.

(4)

(f)
73.
74.

Given that f (x) = 9(cos x) 7 cos x, find the x-coordinate at the point C.

(4)
(Total 20 marks)
A triangle has sides of length 4, 5, 7 units. Find, to the nearest tenth of a degree, the size of the largest angle.
(Total 4 marks)
O is the centre of the circle which has a radius of 5.4 cm.

2
The area of the shaded sector OAB is 21.6 cm . Find the length of the minor arc AB.
(Total 4 marks)
75.

The circle shown has centre O and radius 6.

vector

is the vector

is the vector

and

is the

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 22 of 23

IB Math SL1: Trig Practice Problems

(a)

Alei - Desert Academy

Verify that A, B and C lie on the circle.

(3)

(b)

Find the vector

.
(2)

(c)

Using an appropriate scalar product, or otherwise, find the cosine of angle

.
(3)

(d)

Find the area of triangle ABC, giving your answer in the form a

, where a

.
(4)
(Total 12 marks)

76.

2
2
Solve the equation 3 sin x = cos x, for 0 x 180.

77.

(Total 4 marks)
The diagrams show a circular sector of radius 10 cm and angle radians which is formed into a cone of slant
height 10 cm. The vertical height h of the cone is equal to the radius r of its base. Find the angle radians.

78.

The diagram shows the graph of the function f given by

(Total 4 marks)
f (x) = A sin

+ B,

for 0 x 5, where A and B are constants, and x is measured in radians.

The graph includes the points (1, 3) and (5, 3), which are maximum points of the graph.
(a)
Write down the values of f (1) and f (5).
(2)
(b)

Show that the period of f is 4.

(2)

The point (3, 1) is a minimum point of the graph.

(c)
Show that A = 2, and find the value of B.
(5)
(d)

Show that f (x) = cos

.
(4)

The line y = k x is a tangent line to the graph for 0 x 5.

(e)
Find
(i)
the point where this tangent meets the curve;
(ii)
the value of k.
(6)
(f)

Solve the equation f (x) = 2 for 0 x 5.

(5)
(Total 24 marks)

Macintosh HD:Users:balei:Dropbox:Desert:SL:3Trig:LP_SL1Trig12-13.doc on 03/25/2013 at 7:52 AM

Page 23 of 23