Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience For Home Energy Management System
Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience For Home Energy Management System
Uploaded by
sulthan_81Copyright:
Available Formats
Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience For Home Energy Management System
Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience For Home Energy Management System
Uploaded by
sulthan_81Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Copyright:
Available Formats
Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience For Home Energy Management System
Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience For Home Energy Management System
Uploaded by
sulthan_81Copyright:
Available Formats
316 IEEE Transactions on Consumer Electronics, Vol. 59, No.
2, May 2013
Contributed Paper
Manuscript received 03/30/13
Current version published 06/12/13
Electronic version published 06/12/13. 0098 3063/13/$20.00 2013 IEEE
Smart Heating and Air Conditioning Scheduling
Method Incorporating Customer Convenience
for Home Energy Management System
Hyung-Chul Jo, Sangwon Kim, and Sung-Kwan Joo, Member, IEEE
Abstract A Home Energy Management System (HEMS)
is expected to be vital for saving energy costs considering the
time-varying price of electric power in a smart home
environment. Studies on various energy resources such as
energy storage systems and fuel cells in a smart home
environment are required for HEMS development. In the area
of the HEMSs, however, there exists very limited research on
heating and air conditioning scheduling incorporating
customer convenience. This paper presents a smart heating
and air conditioning scheduling method for HEMS that
considers customer convenience as well as characteristics of
thermal appliances in a smart home environment. The
prototype software based on the proposed method for HEMS
is also implemented
1
.
Index Terms Home energy management system, smart
heating and air conditioning scheduling, customer convenience,
energy resource scheduling
I. INTRODUCTION
Time-varying retail pricing schemes are being designed by
utility companies for reducing the increasing energy demand.
A Home Energy Management System (HEMS) [1]-[5] can
play an important role in saving the energy costs considering
the time-varying price of electric power in a smart home.
Wireless communication networks that control and monitor
appliances in a smart home have been studied. HEMSs that
incorporate communication technologies for reducing energy
costs have been developed. In [6] and [7], a model and an
algorithm for a HEMS for coordinating the operating schedule
of a few devices in a building and a micro-grid were
proposed; however, electric vehicle (EV), fuel cell (FC), and
energy storage system (ESS) lifetime were not considered.
In addition, very limited research has been conducted in the
area of scheduling algorithms that control thermal appliances
1
This work was supported by the Human Resources Development of the
Korean Institute of Energy Technology Evaluation and Planning (KETEP)
grant funded by the Korea government Ministry of Knowledge Economy
(No.20114010203010)
H. -C. Jo is with the School of Electrical Engineering, Korea University,
Seoul, 136-701, Republic of Korea (e-mail: linge2002@korea.ac.kr).
S. Kim is with Future IT R&D Lab., LG electronics, Seoul, Republic of
Korea (e-mail: sangwon3.kim@lge.com).
S. -K. Joo is with the School of Electrical Engineering, Korea University,
Seoul, 136-701, Republic of Korea (e-mail: skjoo@korea.ac.kr)
in a smart home environment, such as heating, ventilating, and
air-conditioning (HVAC) systems, which consume more
energy than others appliances in a home. HVAC models, such
as a model considering outdoor environment information [8]
and a resistance-capacitance equivalent model considering
building structure [9], for thermal energy management in a
building have been proposed. However, these HVAC models
are highly complicated for use in a HEMS and it is difficult to
obtain the information necessary for the model from the smart
home.
This paper presents a reduced HVAC model that can be
applied to the scheduling problem in a HEMS. The proposed
model is based on an ideal model that considers the customer
convenience and characteristics of the HVAC system. For
improving the practicality of the model, parameters related to
indoor heat capacity and heat energy dissipation are estimated
statistically from historical data.
Scheduling problem with energy resource models in a smart
home can be formulated as a mixed integer non-linear
programming (MINLP) problem. The formulation is non-
convex owing to bilinear constraints. The nonlinear, non-
convex nature of the problem affects a significant reduction in
the convergence ratio of the problem and makes it difficult to
arrive at the global optimal solution. In general,
transformation techniques [10]-[12] have been applied to the
original problem for overcoming bilinearity and obtaining a
global optimal solution to the problem. In [13], a
parameterization method was used to the scheduling problem.
Because the method is based on the search tree, the
optimization time of the problem may be longer. Therefore, in
this paper, a linear transformation [12] and optimization
technique is proposed for determining the optimal operating
schedule of the energy resources.
Furthermore, the prototype software based on the proposed
method for HEMs has been developed. In order to determine
the least-cost energy schedules for a smart home, the
implemented software has four modules such as a data input
module, a parameter estimation module, a scheduling module,
and a database management module.
This paper is organized as follows. First, in Section II, a
model considering the HVAC system characteristics and
customer convenience is proposed, and the HEMS scheduling
problem is formulated. In Section III, a method using linear
H.-C. Jo et al.: Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience for Home Energy Management System 317
transformation and optimization is proposed for solving the
scheduling problem for the HEMS. Section IV describes the
implementation of the prototype software. The numerical
results are analyzed to show the effectiveness of the proposed
method in Section V, and the conclusions of this study are
presented in Section VI.
II. HEATING AND AIR CONDITIONING SCHEDULING
PROBLEM WITH CUSTOMER CONVENIENCE FOR SMART
HOME
A method for the integrated scheduling of all energy
resources in the home is required so that customers can reduce
the overall energy cost through the introduction of a smart home
and time-varying price. Fig. 1 shows the overview of HEMS in
a smart home environment. The energy resources are restricted
to a power grid, photovoltaic (PV) system, ESS, EV, FC, and
HVAC because it is impossible to control all the equipment in a
smart home environment without causing inconvenience to the
customer. In this study, several profiles and parameters are
assumed to be known from forecasts based on the historical data
and information obtained from utility companies.
Fig. 1. Overview of HEMS in a smart home environment.
Models of the equipment such as ESS, FC, and EV that
have been studied with regard to the large-scale power system
or building can be applied to the HEMS. HVAC models
almost similar to a real HVAC system were proposed in [8]
and [9]. However, these HVAC models require additional
information that is difficult to obtain within the home
environment. A reduced and practical HVAC model that can
be applied to a HEMS is required. Therefore, a model that
considers the characteristics of the HVAC system and
customer convenience is used in this study.
A. HVAC Model
It is difficult for a customer to frequently modify the HVAC
setting for reducing energy cost considering the time-varying
price. Therefore, the HVAC system is assumed to have an
automatic control system that uses the control signal obtained
from the HEMS scheduling module. An HVAC model for
scheduling the operation mode and output by considering the
temperature and time-varying price is proposed.
The utility companies provide the information about the
coefficient of performance (COP) which represents the ratio of
change in heat to supplied electrical demand. Therefore, a
HVAC model is typically expressed as follows:
) ( ) ( t p COP t q
HVAC HVAC
= (1)
where q
HVAC
(t) is the cooling or heating demand generated by
the HVAC system at time t and p
HVAC
(t) is the electrical demand
of the HVAC system at time t.
For estimating the HVAC systems power demand, the
cooling and heating demands should be calculated considering
the COP and temperature in the discrete time domain.
The indoor cooling or heating demand, according to the first
law of thermodynamics, is expressed as follows:
)} ( ) ( }{ ) ( ) {(
)} ( ) 1 ( { ) (
t T t T t Z
t T t T t q
in out off HVAC off on
in in load
+
+ + =
| | |
o
(2)
where q
load
(t) is the cooling or heating demand at time t; T
in
(t) is
the indoor temperature at time t; T
out
(t) is the outdoor
temperature at time t; Z
HVAC
(t) is a variable denoting the HVAC
system operation at time t; is the indoor heat capacity; and
on
and
off
are parameters related to the outdoor temperature.
The proposed model is considered as ideal if it is applied to
the scheduling problem without correcting the value. For
improving the practicality of the model, the estimated value
must be close to the actual value. For that reason, a method to
update the value with the historical data is adopted.
B. Customer Convenience
For minimizing overall energy cost, the HVAC system
should not be operated when the home is unoccupied. An
estimate of house occupancy is required for determining the
HVAC operating time. To this end, algorithms based on the
customers manual selection or using sensors have been
commercialized. The nonintrusive load monitoring (NILM) [14]
can be used as an alternative method for estimating the time for
which a house remains unoccupied. The NILM is a process for
analyzing changes in the power or voltage supplied to a house,
as shown in Fig. 2, and for detecting the appliances that are used
in the house as well as the total energy consumption.
Fig. 2. Overview of the prototype NILM system.
318 IEEE Transactions on Consumer Electronics, Vol. 59, No. 2, May 2013
If the method based on the manual selection is not used, the
customer occupancy can be statistically estimated by analyzing the
information for the energy consumption of each appliance provided
by the sensors or the algorithm based on the NILM.
Because the temperature in the home decided by the scheduling
may be so high or low that the customer feels inconvenience, the
indoor temperature should be limited to the preferred temperature
established by the customer within the HVAC operating time S.
This requirement can be expressed as follows:
S t T t T T
in
e s s , ) (
max min
(3)
where T
min
and T
max
are the minimum and maximum values,
respectively, of the indoor temperature.
C. Mathematical Model for Scheduling Problem
In this section, the objective function and constraints for the
home appliances based on the aforementioned model and the
formulation described in [6]-[7], are formulated as follows:
1) Objective function
The objective of the scheduling problem is to minimize the
overall energy cost incorporating the costs of electricity and
natural gas. The objective function partially considers the
ESS lifetime, and can be expressed as follows:
| |
=
+ +
24
1
) ( ) ( ) ( ) ( ) (
t
bo b gas grid
t Z BP t p NP t V t EP t p Min (4)
where p
grid
(t) is the power bought from the power grid or sold
to the grid at time t; EP(t) is the electricity price at time t;
V
gas
(t) is the volume of natural gas used by the FC at time t;
NP is the natural gas price; p
b
(t) is the power of the ESS
charging or discharging at time t; BP is the penalty value for
ESS discharging based on the Ah-throughput model [15]; and
Z
bo
(t) is a binary variable denoting the discharging state.
2) Constraints for ESS and EV
The EV model is based on the ESS model, and the
automotive characteristics of the EV are considered.
- SOC dynamics
b
b
Cap
t p
t SOC t SOC
) (
) ( ) 1 ( + = + (5)
where SOC(t) is the state of charge (SOC) in the ESS or the
EV at time t; and Cap
b
denotes the capacity of the ESS or the
EV.
- ESS and EV capacity limits
max min
) ( SOC t SOC SOC s s (6)
where SOC
min
and SOC
max
are the minimum and the maximum
SOC, respectively, of the ESS or the EV.
- Target SOC (only EV)
tar final
SOC t SOC = ) ( (7)
where t
final
denotes the expected departure time of the EV; and
SOC
tar
is the target SOC.
- ESS and EV charger limits
{ } 0 ], , [ ], , [ ) (
max min max min
bi bi bo bo b
P P P P t p e (8)
where
min
bi
P and
max
bi
P are the minimum and the maximum
charging power, respectively, of the ESS or EV charger; and
min
bo
P and
max
bo
P denote the minimum and the maximum
discharging power of the ESS charger only.
3) FC Constraints
Given its role as a small cogeneration unit, the FC generates
heat as a by-product. FC characteristics can be formulated as
the combined heat and power system model proposed in [7].
- Volume of natural gas used by FC
nor elec
FC
gas
q Ef
t p
t V
=
) (
) ( (9)
where p
FC
(t) is the power generated by the FC; Ef
elec
is the
electrical efficiency of the FC; and q
nor
is the energy per unit
volume of natural gas.
- Quantity of heat energy generated by FC
) (
) 1 (
) ( t p
Ef
Ef Ef
t q
FC
elec
elec heat
FC
= (10)
where q
FC
(t) is the heat energy generated by the FC at time t;
and Ef
heat
is the FCs thermal efficiency.
- FC generation limits
{ } 0 ], , [ ) (
max min
FC FC FC
P P t p e (11)
where
min
FC
P and
max
FC
P are the minimum and the maximum
power generated by the FC, respectively.
4) HVAC system constraints
- Heat balance
) ( ) ( ) ( t p COP t q t q
HVAC FC load
+ = (12)
} , { )}, ( ) 1 ( {
} ) ( ) {( )} ( ) ( { ) (
, , ,
FC HVAC E t T t T
t Z t T t T t q
in in
E i
off i i off i on i in out load
e + +
+ =
e
o
| | |
(13)
where
i,on
and
i,off
are the values in the operating state and
non-operating state of the thermal device i, respectively.
- Customer-preferred temperature
S t T t T T
in
e s s , ) (
max min
(14)
- HVAC power consumption limits
{ } 0 ], , [ ) (
max min
HVAC HVAC HVAC
P P t p e (15)
where
min
HVAC
P and
max
HVAC
P are the minimum and the maximum
electrical demand of the HVAC system, respectively.
5) Power balance constraints
) ( ) ( ) ( ) ( ) ( ) ( t p t p t p t p t p t p
load HVAC b FC solar grid
+ + = + + (16)
where p
solar
(t) is the power supplied by the PV at time t; and p
load
(t)
is the total demand from the uncontrolled appliances at time t.
III. SMART HEATING AND AIR CONDITIONING
SCHEDULING METHOD FOR HEMS
The solution to the problem formulated as an MINLP using
the above-described model could be global or local optimum
depending on problem convexity. Constraint (13) is non-
convex owing to the sum of the bilinear terms. Therefore, it is
necessary to verify that the obtained solution is globally
optimal. Owing to the complexity of this process, the problem
must be converted into a convex form through convexification.
A number of methods to transform a non-convex constraint
into a convex one have been discussed. In this study, an easy-
H.-C. Jo et al.: Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience for Home Energy Management System 319
to-implement linear transformation technique is adopted [11].
Constraint (13) can be rewritten in a linear form using a set
of slack variables X(t) for the T
in
(t) variables as follows:
} , { )}, ( ) 1 ( { )] (
) ( ))} ( 1 ( ) ( ){ ( [ ) (
2 , ,
1 , , , ,
FC HVAC E t T t T t X
t X t Z t Z t T t q
in in i off i
i on i
E i
i off i i on i out load
e + +
+ =
e
o |
| | |
(17)
The bilinear term in constraint (13) can be substituted by
the slack variables. Constraints (18)(23) are added to define
the new variables required for the transformation.
)) ( 1 ( ) ( ) ( )) ( 1 ( ) (
max 1 , min 1 ,
t Z K t X t T t Z K t X
i i in i i
+ s s (18)
) ( ) ( ) ( ) ( ) (
max 2 , min 2 ,
t Z K t X t T t Z K t X
i i in i i
+ s s (20)
) ( ) ( ) (
max 1 , min
t Z K t X t Z K
i i i
s s (21)
)) ( 1 ( ) ( )) ( 1 (
max 2 , min
t Z K t X t Z K
i i i
s s (22)
E i e (23)
where K
min
and K
max
are, respectively, the lower and the upper
bounds of T
in
(t).
The difference between K
min
and K
max
should be as small as
possible. For satisfying constraint (14), K
min
should be lower
than T
min
and K
max
should be greater than T
max
. For selecting
appropriate K
min
and K
max
values, historical T
in
(t) data are used.
Fig. 3 presents the proposed scheduling method for HEMS.
The entire problem is written in a linear form by replacing the
nonconvex constraint (13) with a linear one (17) and by
adding constraints (18)(23). For solving the problem, first,
the profiles and parameters obtained from the forecast
algorithm are entered into the scheduling problem. K
min
, K
max
,
, and HVAC operating time S are estimated from the
historical data. Additionally, the preferred temperature is
selected manually by the customer or from the estimation
results using past selections. The optimal scheduling result can
be obtained by solving the modified formulation.
Fig. 3. The proposed scheduling method for HEMS.
IV. IMPLEMENTATION OF PROTOTYPE SOFTWARE USING
SMART HEATING AND AIR CONDITIONING SCHEDULING
METHOD WITH CUSTOMER CONVENIENCE FOR HEMS
The prototype software using the proposed method has
been developed using a commercially available, cross-
platform optimization suite. It performs optimization for
scheduling of energy resources and manages the scheduling
results. Fig. 4 shows a configuration of the proposed prototype
software for smart heating and air conditioning scheduling
system. The software is composed of four modules that
include a data input module, a parameter estimation module, a
scheduling module, and a database management module.
Fig. 4. Middleware Architecture of the proposed HEMS.
A. Data Input Module
As shown in Fig. 5, the module collects the data that is
directly input to the software by the customer or transmitted
from the prediction modules. The customer can enter
information related to the customer convenience for HVAC
and EV into the software through the interface manager. The
rest of the essential information is obtained from the
prediction modules. The collected information is stored in the
database.
Fig. 5. Screenshot of data input in the implemented prototype software.
B. Parameter Estimation Module
This module is designed to estimate the parameters from the
historical data in the database. As mentioned in the previous
sections, and K values are necessary to solve the proposed
problem. Given the value estimated from the volume and mass
320 IEEE Transactions on Consumer Electronics, Vol. 59, No. 2, May 2013
of indoor air, can be statistically estimated using equation (2)
and historical data, as shown in Fig. 6. The output power of the
device for smart heating and air conditioning, the indoor
temperature, and the outdoor temperature constitute the
historical data. If necessary, can also be estimated using a
constant value via a process similar to that shown in Fig. 6.
Fig. 6. estimation procedure for the proposed method for HEMS.
For selecting the appropriate value of K, the candidates of K
are determined by analyzing the historical data. Furthermore,
the preferred temperature and the candidates are compared to
determine the value of K. The parameters selected by the
estimation engine are transmitted to the scheduling module.
C. Scheduling Module
This module is designed to obtain the schedule of the
energy resources using the proposed method and input data. It
is operated when press the solve button. Given that the values
of , , and K are estimated by the parameter estimation
module, optimization based on the branch and bound
algorithm can be performed to obtain the optimal schedule.
D. Database Management Module
The input data and the optimal solution from the scheduling
method is stored in the database through database
management module and displayed, as shown in Fig. 7. Data
that can be displayed in the software include the electrical
demand for the uncontrolled appliances, PV output, prices of
various energy resources, HVAC operation, EV charging, FC
operation, and ESS charging/discharging.
Fig. 7. Screenshot for displaying total energy consumption and electric
energy of energy device.
V. NUMERICAL RESULTS
For testing the proposed method, a scenario based on the
data collected from several institutions during winter is
created. A smart home with a volume of 1,145 m
3
is
assumed for the simulation. It is also assumed that two
adult occupants have a full-time job and the unoccupied
period to be statistically estimated is from 08:30 am to
19:00 pm. The energy resources in the smart home
environment include the PVs, FCs, ESS, EV, HVAC, and
the uncontrolled appliances. Several parameters of each
device to be assumed are listed in Table I. The preferred
operating time of HVAC and EV charging time to be
assumed in Table I is based on the unoccupied period. The
value of is estimated from the volume and mass of the
indoor air. The historical data for the estimation of are
obtained from the library building.
TABLE I
SPECIFICATION OF ENERGY RESOURCES IN SMART HOME
Energy Resource Specification
Energy storage system
Capacity 10 kWh
Maximum battery
charge/discharge
6 kWh
Electric vehicle
Capacity 16.4 kWh
Maximum battery
charge/discharge
3.3 kWh
Charging time 19 pm7 am
Fuel cell
Capacity 1 kW
0.03 (not operated)
0.04 (operated)
Efficiency
40% (electricity)
45% (heat)
Heating, ventilating, and
air conditioning
COP 2.73
0.03 (not operated)
0.55 (operated)
Preferred operating
time of HVAC
19 pm 9 am
Preferred
temperature
19C
The several profiles used in this study are shown in Fig. 8.
Fig. 8 (a) shows the electrical demand profile forecasted from
the electrical energy consumption data of the uncontrolled
appliances and the occupied period. Fig. 8 (b) shows the 3-
kWh PV generation profile. For developing the PV generation
profile, the PV output power data to be obtained from the PV
cell in the school building is used. The prices of natural gas,
power bought from the utility, power sold to the utility, and
BP are shown in Fig. 8 (c). The electricity price and natural
gas price are, respectively, based on the time-of-use (TOU)
and natural gas rate for the cogeneration of the utility in
America. The BP is determined by using the ESS price and
the amount of discharge during the lifetime. For the
calculation of the amount of ESS discharge during the lifetime,
it is assumed that the ESS lifecycle at 80% depth of discharge
(DOD) is 3,000 cycle.
H.-C. Jo et al.: Smart Heating and Air Conditioning Scheduling Method Incorporating Customer Convenience for Home Energy Management System 321
Fig. 8. (a) Electrical demand profile, (b) PV generation profile, (c) Prices
profile of various resources.
Based on several parameters and profiles, the smart heating
and air conditioning scheduling method for HEMS provides a
smart home with an optimal schedule for each energy resource.
The total electrical demand incorporating the demands of
HVAC and ESS charging and electrical energy resource
composition are shown in Fig. 9. As can be seen in the figure,
only the FC is operated when natural gas price is lower than
electricity price. For generating profit using a BP lower than
the TOU, the ESS is discharged at 20:00. In fact, during peak
hours, all energy supplying resources are used for decreasing
the amount of energy purchased from the grid.
Fig. 9. Total electrical demand and composition of electrical energy
supplies in smart home.
As shown in Fig. 10, the proposed HVAC model is
successfully applied to the scheduling problem. There is no
preheating in the unoccupied period, during which the
electricity price is at its peak. In contrast, the HVAC system is
operated within the preferred temperature during the occupied
period. Furthermore, owing to constant indoor temperature, as
shown in Fig. 10, it can be observed that the part representing
the indoor temperature dynamics in constraint (13) is ignored,
and the HVAC output power is proportional to the difference
between the outdoor and indoor temperatures.
Fig. 10. Scheduling result for the HVAC operation and the indoor
temperature change at constant preferred temperature in smart home.
Setting different values of the preferred temperature in the
method could have an effect on the overall energy cost. The
cases with several different T
min
and T
max
values are compared
to demonstrate the influence of preferred temperature on the
overall energy cost in the smart home environment. The
preferred temperatures in all these cases are listed in Table II.
In cases I, II, and III, the preferred temperature of each case is
respectively 19C, 20C, and 21C. In contrast, in case IV, the
preferred temperature is determined for the indoor temperature
to be in a range of 19C to 21C for preventing customer
inconvenience.
TABLE II
PREFERRED TEMPERATURE
Case Temperature (C)
Case I 19
Case II 20
Case III 21
Case IV 1921
It can be observed from the results shown in Fig. 11 that the
overall energy cost can be reduced by setting the preferred
indoor temperature within a specific range rather than as a
constant value while avoiding inconvenience to the customer.
The overall energy cost in the case IV is respectively 28%,
32%, and 36% lower than other cases. Furthermore, in case of
the constant preferred temperature, the overall energy cost
increases by approximately 3% when the constant preferred
temperature increases by 1C.
322 IEEE Transactions on Consumer Electronics, Vol. 59, No. 2, May 2013
Fig. 11. Comparison of overall energy cost for various preferred
temperatures.
VI. CONCLUSION
This paper proposes a smart heating and air conditioning
method with customer convenience for HEMS. Optimal
scheduling various energy resources in a smart home is
needed to save energy costs. This paper describes a reduced
HVAC model that considers customer convenience and a
method for solving the scheduling problem of the HEMS with
the reduced HVAC model. The HEMS based on the proposed
method can be used to determine the least-cost schedules of
the available energy resources while minimizing
inconvenience to the customer in a smart home environment.
The numerical results show that the HEMS based on the
proposed scheduling method, which can be installed at various
smart homes, has great potential to reduce customers overall
energy costs.
REFERENCES
[1] M. Inoue, T. Higuma, Y. Ito, N. Kushiro and H. Kubota, Network
Architecture for Home Energy Management System, IEEE Trans.
Consumer Electron., vol. 49, no. 3, pp. 606-613, Aug. 2003.
[2] C. Y. Leong, A. R. Ramli, and T. Perumal, A Rule-Based Framework
for Hetegeneous Subsystems Management in Smart Home
Environment, IEEE Trans. Consumer Electron., vol. 55, no. 3, pp.
1208-1213, Aug. 2003.
[3] Y. S. Son, T. Pulkkinen, K. D. Moon, and C. Kim, Home Energy
Management System based on Power Line Communication, IEEE
Trans. Consumer Electron., vol. 56, no. 3, pp. 606-613, Aug. 2010.
[4] D. M. Han and J. H. Lim, Smart Home Energy Management System
using IEEE 802.15.4 and ZigBee, IEEE Trans. Consumer Electron.,
vol. 56, no. 3, pp. 1403-1410, Aug. 2010.
[5] J. Han, C. S. Choi and I. Lee, More Efficient Home Energy
Management System Based on ZigBee Communication and Infrared
Remote Controls, IEEE Trans. Consumer Electron., vol. 57, no. 1, pp.
85-89, Feb. 2011.
[6] C. Chen, S. Duan, T. Cai, B. Liu, and G. Hu, Smart energy management
system for optimal microgrid economic operation, IET Renew. Power
Gener., vol. 5, no. 3, pp. 258-267, 2011.
[7] X. Guan, Z. Xu, and Q. S. Jia, Energy-efficient buildings facilitated by
microgrid, IEEE Trans. Smart Grid, vol. 1, no. 3, pp. 243-252, Dec.
2010.
[8] B. Syn, P. B. Luh, Q. S. Jia, Z. Jiang, F. Wang, and C. Song, An
integrated control of shading blinds, natural ventilation, and HVAC
systems for energy saving and human comfort, The 6
th
Annu. IEEE
Conf. Autom. Sci. Eng., Toronto, ON, Canada, Aug. 21-24, 2010.
[9] K. Deng, P. Barooah, P. G. Mehta, and S. P. Meyn, Building thermal
model reduction via aggregation of states, ACC, pp. 5118-5123, 2010.
[10] I. Harjunkoski, T. Westerlund, R. Prn, and H. Skrifvars, Different
transformations for solving non-convex trim-loss problems by MINLP,
Euro. J. of Operational Res., vol. 105, no. 3, pp. 594-603, Mar. 1998.
[11] T. Westerlund, I. Harjunkoski, and J. Isaksson, Solving a production
optimization problem in a paper-converting mill with MILP, Com. and
Chem. Eng., vol. 22, no. 4-5, pp. 563-570, 1998.
[12] I. Harjunkoski, T. Westerlund, and R. Prn, Numerical and
environmental considerations on a complex industrial mixed integer
non-linear programming (MINLP) problem, Com. and Chem. Eng., vol.
23, no. 10, pp. 1545-1561, Dec. 1999.
[13] H. -C. Jo, S. Kim, and S. -K. Joo, Smart heating and air conditioning
scheduling with customer convenience in a home energy management
system, Int. Conf. Consumer Electron., Jan. 2013.
[14] S. Gupta, M. S. Reynolds, and S. N. Patel, ElectricSense: single-point
sensing using EMI for electrical event detection and classification in the
home, Conf. Ubiq. Computing, pp. 139-148. 2010.
[15] S. Drouilhet and B. L. Johnson, A battery life prediction method for
hybrid power applications, U.S. Dept. Energy, Chicago, IL, Contract
DE-AC36-83CH10093, Jan. 1997.
BIOGRAPHIES
Hyung-Chul Jo received his B.S. degree in the school of Electrical
Engineering from Korea University, Seoul, in 2010. He is currently pursuing
his Ph.D. degree at Korea University. His research interests include smart
home and building energy management systems and large- and small-scale
system optimization.
Sang-Won Kim received his B.S. degree from Seoul National University,
Seoul, Korea in 2002 and M.S. degree from Korea University in 2013. Since
2002, he has been with LG Electronics, Seoul, Korea, where he is
currently a Senior Research Engineer in the Future IT R&D Lab.
His main research interests include data mining and optimization algorithms
for smart homes and buildings.
Sung-Kwan Joo (M05) received his M.S. and Ph.D. degrees from the
University of Washington, Seattle, in 1997 and 2004, respectively. From 2004
to 2006, he was an Assistant Professor in the Department of Electrical and
Computer Engineering at North Dakota State University, Fargo, U.S. He is
currently an Associate Professor in the School of Electrical Engineering at
Korea University, Seoul, Korea. His research interests include
multidisciplinary research related to energy systems, involving information
technologies, optimization, and intelligent systems.
You might also like
- API API-580 Exam Tutorial: Showing 1-20 of 140 Questions Next (Page 1 Out of 7)Document54 pagesAPI API-580 Exam Tutorial: Showing 1-20 of 140 Questions Next (Page 1 Out of 7)Arty Pin100% (14)
- Systems Analysis and Design - TemplateDocument4 pagesSystems Analysis and Design - Templateyucolujob0% (1)
- Sabp A 009Document208 pagesSabp A 009sethu1091100% (2)
- Unit PsaDocument14 pagesUnit Psasulthan_81100% (1)
- On Philosophical Style by Brand BlandshardDocument17 pagesOn Philosophical Style by Brand Blandshardenieves78100% (1)
- Cognitive-Behavioral Treatment of Women's Body-Image DissatisfactionDocument9 pagesCognitive-Behavioral Treatment of Women's Body-Image DissatisfactionAnda F. CotoarăNo ratings yet
- Minimizing Building Electricity Costs in A Dynamic Power Market: Algorithms and Impact On Energy ConservationDocument11 pagesMinimizing Building Electricity Costs in A Dynamic Power Market: Algorithms and Impact On Energy ConservationRene Daniel Rolon FleitasNo ratings yet
- Adaptive Prediction Model Accuracy in The Control of Residential Energy ResourcesDocument6 pagesAdaptive Prediction Model Accuracy in The Control of Residential Energy ResourcesMario SammyNo ratings yet
- Smart Residential Load Simulator For Energy Management in Smart GridsDocument10 pagesSmart Residential Load Simulator For Energy Management in Smart GridsIsmael JaramilloNo ratings yet
- Srls (Smart Residential Load Simulator)Document8 pagesSrls (Smart Residential Load Simulator)Dulal MannaNo ratings yet
- Sizing of Residential CHP Systems: Energy and BuildingsDocument11 pagesSizing of Residential CHP Systems: Energy and BuildingsMaxim MendelNo ratings yet
- Energy and Buildings: Heejin Cho, Rogelio Luck, Sandra D. Eksioglu, Louay M. ChamraDocument7 pagesEnergy and Buildings: Heejin Cho, Rogelio Luck, Sandra D. Eksioglu, Louay M. ChamrapantoleNo ratings yet
- Energies: Smart Home Energy ManagementDocument5 pagesEnergies: Smart Home Energy ManagementVIKRAM K 14PHD0358No ratings yet
- A New Design Guideline For The HeatingDocument12 pagesA New Design Guideline For The HeatingHatef HajianNo ratings yet
- Salerno 2021Document41 pagesSalerno 2021Umar RahmanNo ratings yet
- Renewable and Sustainable Energy ReviewsDocument15 pagesRenewable and Sustainable Energy ReviewsDhanada MishraNo ratings yet
- Energies: Occupancy-Based HVAC Control With Short-Term Occupancy Prediction Algorithms For Energy-Efficient BuildingsDocument20 pagesEnergies: Occupancy-Based HVAC Control With Short-Term Occupancy Prediction Algorithms For Energy-Efficient BuildingsbambangNo ratings yet
- Heat Exchanger Network Optimization Using Integrated Specialized Software From ASPENTECH and GAMS TechnologyDocument6 pagesHeat Exchanger Network Optimization Using Integrated Specialized Software From ASPENTECH and GAMS TechnologyCatlinhbk08No ratings yet
- Thang2018 Article OptimalOperationOfEnergyHubInCDocument12 pagesThang2018 Article OptimalOperationOfEnergyHubInCHeri Tamtowi SyaputroNo ratings yet
- An Application of A Soft Real-Time Genetic Algorithm For HVAC System ControlDocument11 pagesAn Application of A Soft Real-Time Genetic Algorithm For HVAC System ControlInternational Journal of Application or Innovation in Engineering & ManagementNo ratings yet
- Balancing Energy Consumption and Thermal Comfort in Buildings: A Multi-Criteria FrameworkDocument27 pagesBalancing Energy Consumption and Thermal Comfort in Buildings: A Multi-Criteria FrameworkSoham SarpotdarNo ratings yet
- HVAC System Optimization For Energy Management by Evolutionary ProgrammingDocument12 pagesHVAC System Optimization For Energy Management by Evolutionary ProgrammingEsmining MitarumNo ratings yet
- 1 s2.0 S0360544221019794 MSNDocument15 pages1 s2.0 S0360544221019794 MSNArnob DasNo ratings yet
- Parameter Estimation of Internal Thermal Mass of Building Dynamic Models Using Genetic Algorithm 2005 PDFDocument15 pagesParameter Estimation of Internal Thermal Mass of Building Dynamic Models Using Genetic Algorithm 2005 PDFSathiaram RamNo ratings yet
- HVAC Control Strategies To Enhance Comfort and Minimise Energy UsageDocument11 pagesHVAC Control Strategies To Enhance Comfort and Minimise Energy UsageArun AbNo ratings yet
- Optimal Scheduling of Smart Homes AppliancesDocument4 pagesOptimal Scheduling of Smart Homes Appliancesjorbol827No ratings yet
- Imp 3Document20 pagesImp 3muhammd umerNo ratings yet
- Control Strategies For Energy Optimization of HVAC Systems in Small Office Buildings Using EnergyPlusTMDocument6 pagesControl Strategies For Energy Optimization of HVAC Systems in Small Office Buildings Using EnergyPlusTMvedant khapekarNo ratings yet
- Development and Evaluation of A Generalized Rule-Based Control Strategy For Residential Ice Storage SystemsDocument13 pagesDevelopment and Evaluation of A Generalized Rule-Based Control Strategy For Residential Ice Storage SystemsArnob DasNo ratings yet
- Isdb ProposalDocument74 pagesIsdb Proposaloleolo ibrahimNo ratings yet
- Investigation of Model Predictive Control For Fifth Generation District Heating and Cooling (5GDHC) SubstationsDocument11 pagesInvestigation of Model Predictive Control For Fifth Generation District Heating and Cooling (5GDHC) SubstationsSimone BuffaNo ratings yet
- Sensors: Power Factor Compensation Using Teaching Learning Based Optimization and Monitoring System by Cloud Data LoggerDocument23 pagesSensors: Power Factor Compensation Using Teaching Learning Based Optimization and Monitoring System by Cloud Data LoggerDungNo ratings yet
- Kang 2014Document10 pagesKang 2014hadiNo ratings yet
- Design and Optimization of District Energy SystemsDocument6 pagesDesign and Optimization of District Energy Systemsduplicado2012No ratings yet
- Energies 12 02058 PDFDocument24 pagesEnergies 12 02058 PDFchaudharymeelNo ratings yet
- Using Pinch Technology in Operations?: Zoran Milosevic, Allan Rudman and Richard Brown KBC Process Technology, UKDocument13 pagesUsing Pinch Technology in Operations?: Zoran Milosevic, Allan Rudman and Richard Brown KBC Process Technology, UKsohail1985100% (2)
- Optimizing Power ConsumptionDocument22 pagesOptimizing Power Consumptionsriletsoin03No ratings yet
- Mathews 2000Document25 pagesMathews 2000Arindom RayNo ratings yet
- Hvac ThesisDocument5 pagesHvac Thesisbookslover1No ratings yet
- Management and Control of Domestic Smart Grid TechnologyDocument11 pagesManagement and Control of Domestic Smart Grid TechnologyJunaid AhmedNo ratings yet
- Home Energy Management System ThesisDocument4 pagesHome Energy Management System ThesisLisa Riley100% (2)
- Reinforcement Learning-Based BEMS Architecture For Energy Usage OptimizationDocument33 pagesReinforcement Learning-Based BEMS Architecture For Energy Usage Optimizationmariva4703No ratings yet
- Smart GridDocument10 pagesSmart GridAnand SreekumarNo ratings yet
- The Benefits of 8760 Hour-By-Hour Building Energy AnalysisDocument8 pagesThe Benefits of 8760 Hour-By-Hour Building Energy Analysisalialavi2No ratings yet
- Forecasting of Residential Unit's Heat Demands: A Comparison of Machine Learning Techniques in A Real World Case StudyDocument35 pagesForecasting of Residential Unit's Heat Demands: A Comparison of Machine Learning Techniques in A Real World Case StudyAbir SarkarNo ratings yet
- Sensors-20-00781-Version AuteurDocument18 pagesSensors-20-00781-Version Auteuromar ahmedNo ratings yet
- School of Graduate StudyDocument2 pagesSchool of Graduate StudywswrNo ratings yet
- Niu TechnoDocument12 pagesNiu TechnopauloNo ratings yet
- Liu 2016Document12 pagesLiu 2016m.muthu lakshmiNo ratings yet
- Demand Response Whit Functional BuildingDocument6 pagesDemand Response Whit Functional Buildinglu_udgNo ratings yet
- SMC 06 NikolicDocument7 pagesSMC 06 NikolicmanueldidyNo ratings yet
- Building HVAC EstimateDocument11 pagesBuilding HVAC EstimatetmamputsiNo ratings yet
- Buiding Audit Energy ConservationDocument12 pagesBuiding Audit Energy ConservationNaMatazuNo ratings yet
- Energies 12 01926 PDFDocument17 pagesEnergies 12 01926 PDFlahohiNo ratings yet
- IJPUB1802028Document7 pagesIJPUB1802028Neda AarabiNo ratings yet
- 11311-1045962 SilvaDocument18 pages11311-1045962 SilvatimothyhemsleyylaganNo ratings yet
- Pinch White Paper (Rev 3) 2012Document21 pagesPinch White Paper (Rev 3) 2012Energy_ExpertNo ratings yet
- Energy and Buildings: Mohammad Omar Abdullah, Lim Pai Yii, Ervina Junaidi, Ghazali Tambi, Mohd Asrul MustaphaDocument9 pagesEnergy and Buildings: Mohammad Omar Abdullah, Lim Pai Yii, Ervina Junaidi, Ghazali Tambi, Mohd Asrul MustaphaLarry SmithNo ratings yet
- Fuzzy Control For Improved Buildings Energy Management SystemsDocument8 pagesFuzzy Control For Improved Buildings Energy Management Systemsrida.hamza.muhammadNo ratings yet
- Optimization of Hybrid Micro-Cchp Systems in The Day-Ahead Electricity MarketDocument11 pagesOptimization of Hybrid Micro-Cchp Systems in The Day-Ahead Electricity MarketadrianunteaNo ratings yet
- Optimization Control Strategy For A Central Air CoDocument21 pagesOptimization Control Strategy For A Central Air CoHussein SaeedNo ratings yet
- A Simple Procedure To Size Active Solar Heating Schemes For Low-Energy Building DesignDocument9 pagesA Simple Procedure To Size Active Solar Heating Schemes For Low-Energy Building DesignmohammudpNo ratings yet
- PHD Synopsis Accepted SakeenaDocument40 pagesPHD Synopsis Accepted SakeenaYousup AliNo ratings yet
- Thermonet: Fine-Grain Assessment of Building Comfort and E CiencyDocument8 pagesThermonet: Fine-Grain Assessment of Building Comfort and E CiencyMukesh WaranNo ratings yet
- Energy and Thermal Management, Air-Conditioning, and Waste Heat Utilization: 2nd ETA Conference, November 22-23, 2018, Berlin, GermanyFrom EverandEnergy and Thermal Management, Air-Conditioning, and Waste Heat Utilization: 2nd ETA Conference, November 22-23, 2018, Berlin, GermanyChristine JuniorNo ratings yet
- Servlet - Returning Information Received From The ClientDocument7 pagesServlet - Returning Information Received From The Clientsulthan_81No ratings yet
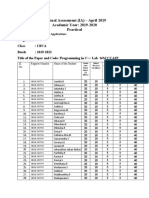
- Internal Assessment (IA) - April 2019 Academic Year: 2019-2020 PracticalDocument2 pagesInternal Assessment (IA) - April 2019 Academic Year: 2019-2020 Practicalsulthan_81No ratings yet
- R.Punitha Research ScholarDocument18 pagesR.Punitha Research Scholarsulthan_81No ratings yet
- Operating Systems For BcaDocument5 pagesOperating Systems For Bcasulthan_81No ratings yet
- 4.gaussain MixtureDocument6 pages4.gaussain Mixturesulthan_81No ratings yet
- Ts 102690v010201pDocument279 pagesTs 102690v010201psulthan_81No ratings yet
- What Are The Quantities Associated With Each Bus in A System?Document2 pagesWhat Are The Quantities Associated With Each Bus in A System?sulthan_81No ratings yet
- Power System Analysis-Unit-5-Q-ADocument4 pagesPower System Analysis-Unit-5-Q-Asulthan_81No ratings yet
- Power System Analysis-Unit-3-Q-ADocument3 pagesPower System Analysis-Unit-3-Q-Asulthan_81No ratings yet
- Mains Differential Equation Sol-1Document14 pagesMains Differential Equation Sol-1sulthan_81No ratings yet
- Outer Space Debris: An International Obligation To Mitigate & ControlDocument17 pagesOuter Space Debris: An International Obligation To Mitigate & ControlarnavNo ratings yet
- KB - ResumeDocument1 pageKB - Resumeapi-633865837No ratings yet
- Observations ChildDocument8 pagesObservations Childmargret angcot100% (1)
- Working Across Cultures and Knowing When To Shut UpDocument16 pagesWorking Across Cultures and Knowing When To Shut UpHelen100% (1)
- Nizatidine Stability Indicating Assay Method HPLC 02Document7 pagesNizatidine Stability Indicating Assay Method HPLC 02Ahmed MosalamNo ratings yet
- Quntitative ResearchDocument20 pagesQuntitative ResearchWinnie Lôla100% (2)
- TOEFL ReadingDocument27 pagesTOEFL Readingni'mah izati atiko putriNo ratings yet
- Teaching Guide Catchup ESP Grade 8Document2 pagesTeaching Guide Catchup ESP Grade 8Cassey SisonNo ratings yet
- University of Agriculture, Faisalabad Faisalabad PakistanDocument3 pagesUniversity of Agriculture, Faisalabad Faisalabad Pakistanمرشد صاحبNo ratings yet
- Safety Net Recovery System PDFDocument2 pagesSafety Net Recovery System PDFIrfan Adi PratomoNo ratings yet
- Calculus Signature Assignment 1 The Mean Value Theorem 1Document2 pagesCalculus Signature Assignment 1 The Mean Value Theorem 1api-331199595No ratings yet
- Time Management SessionDocument3 pagesTime Management SessionAmit KumarNo ratings yet
- Cornelia - Mima Maxey (1933) PDFDocument97 pagesCornelia - Mima Maxey (1933) PDFrodrigo estrasulasNo ratings yet
- Audit Imperatives PT 4Document2 pagesAudit Imperatives PT 4Caterina De LucaNo ratings yet
- Topic 6Document21 pagesTopic 6spica_shie88No ratings yet
- External Auditors' Reliance On Internal Audit in Sri LankaDocument83 pagesExternal Auditors' Reliance On Internal Audit in Sri Lankadilu_0002100% (2)
- Mac vs. PCDocument18 pagesMac vs. PCsleepwlker2410No ratings yet
- Unit-5 Topic-6 Oscillations Answers (End-Of-Chapter & Examzone)Document5 pagesUnit-5 Topic-6 Oscillations Answers (End-Of-Chapter & Examzone)AvrinoxNo ratings yet
- 2018 2019 Supplementary Direct Entry List IiDocument7 pages2018 2019 Supplementary Direct Entry List IiArvin DabasNo ratings yet
- Humanities-A Study On The Technological-Mun Mun Das BiswasDocument6 pagesHumanities-A Study On The Technological-Mun Mun Das BiswasBESTJournalsNo ratings yet
- RC552-FE (A) User Manual 20060824Document25 pagesRC552-FE (A) User Manual 20060824yudi.arfiantoNo ratings yet
- For Stem Assassin's Creed Has A New Mission: Working in The ClassroomDocument6 pagesFor Stem Assassin's Creed Has A New Mission: Working in The ClassroomMikkos AtasNo ratings yet
- Gcse Ocr DT FlashcardsDocument8 pagesGcse Ocr DT Flashcardsapi-256027312No ratings yet
- GpsOne OverviewDocument6 pagesGpsOne OverviewMita ChitaNo ratings yet
- Lecture Notes 9.1Document17 pagesLecture Notes 9.1Yip Tuck WaiNo ratings yet