1

Question 6: Circular Motion

Please remember to photocopy 4 pages onto one sheet by going A3A4 and using back to back on the photocopier


Page
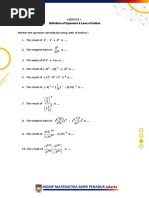
Introduction to formulae

2
Ord. Level Exam Questions: Manipulation-of-equations type questions

3
Particle on a String: Ordinary Level

5
Cones and Spheres: Ordinary Level

8
Cones and Spheres: Higher Level

9
Particles on a string: Higher Level

10
Particle slides off the outside of a sphere

12
Conservation of Energy

13
Beads on a string

13
Friction Force

14
Periodic Time

14
Answers to Ordinary Level Exam Questions

15
Guide to answering Exam Questions: 2008 1997

17


*********** Marking Schemes / Solutions to be provided separately *************


2

Angular Velocity is the rate of change of angle with respect to time.
The symbol for angular velocity is e (pronounced omega).
Mathematically e = u/t

Angular Velocity is measured in radians per second (rad/s), where 2 radians corresponds to a full circle
(360
0
).

A little recap on radians
An angle (in radians) is defined as the arc length divided by the radius, i.e. u = arc length/radius.
For a full circle the arc length is 2r, so in this case u becomes 2 radians. This allows us to convert from
radians to degrees if we need to (2 radians = 360
0
)

Revolutions
If the object is carrying out full revolutions, then the time corresponding to one full revolution is called the
periodic time (symbol T).
Therefore in this case the expression e = u/t becomes e = 2/T

or


If an object is moving in a circle at constant speed, it is accelerating.
This is because while its speed is not changing, its velocity is. Why? Because velocity is defined as speed in
a given direction, so if direction is changing, even though speed is not, then the velocity is changing,
therefore the object is accelerating.

Now for an object undergoing complete revolutions the frequency (f) of oscillation corresponds to the
number of revolutions per second, where f = 1/T
e.g. if the periodic time is 0.2 seconds then the frequency will be 5 (Hertz).

Relationship between Linear Speed (v) and Angular Velocity (e)
Using the relationship velocity = distance travelled/time taken (and for a full circle the distance travelled is
the circumference of a circle = 2r)
v = 2r/T but 2/T = e
v = er


Centripetal Force
The force - acting in towards the centre - required to keep an object moving in a circle is called Centripetal
Force.

Centripetal Acceleration
If a body is moving in a circle then its acceleration towards the centre is called Centripetal Acceleration.

Formulae for Centripetal Acceleration and Centripetal Force


but because v = re we also have




And because F = ma we get and also

a = re
2

F = mre
2

r
mv
F
c
2
=
v = r e

e

e = 2/T
3

Manipulation of equations
2009 (a) [Ordinary Level]
A particle describes a horizontal circle of radius 0.5 m with uniform angular velocity radians per second.
Its acceleration is 8 m/s
2
.
(i) Find the value of
(ii) Find the time taken to complete one revolution.

Solution
(i) re
2
= acceleration
0.5e
2
= 8
e = 4 rad/s

(ii) Periodic time = 2/e
= /2 s.

2008 (a) [Ordinary Level]
A particle describes a horizontal circle of radius 2 metres with constant angular velocity radians per
second.
Its speed is 5 m/s and its mass is 3 kg.
Find
(i) the value of
(ii) the centripetal force on the particle.

Solution
(i) re = v
2e = 5
e = 2.5 rad/s

(ii) Force = mre
2

= (3)(2)(2.5
2
)
= 37.5 N


2007(a) [Ordinary Level]
A particle describes a horizontal circle of radius r m with uniform angular velocity radians per second.
Its speed and acceleration are 2 m/s and 4 m/s
2
respectively.
Find
(i) the value of r
(ii) the value of .

re = 2
re
2
= 4
e(re) = 4
e(2) = 4
e = 2 rad/s
4 = 1 m







4

For You

2010 (a) [Ordinary Level]
A particle describes a horizontal circle of radius r metres with uniform angular velocity radians per
second.
Its speed and acceleration are 6 m s
-1
and 12 m s
-2
respectively.
Find
(i) the value of r
(ii) the value of .


2006 (a) [Ordinary Level]
A particle describes a horizontal circle of radius 2 metres with constant angular velocity radians per
second.
The particle completes one revolution every 5 seconds.
(i) Show that is equal to 2/5.
(ii) Find the speed and acceleration of the particle.
Give your answers correct to one place of decimals.




5

Particle on a String: Ordinary Level













Examples
2006 (b) [Ordinary Level]
A conical pendulum consists of a particle of mass 4 kg attached by a light
inelastic string of length 2 metres to a fixed point p.
The particle describes a horizontal circle of radius r.
The centre of the circle is vertically below p.
The string makes an angle of 30
0
with the vertical.
Find
(i) the value of r
(ii) the tension in the string
(iii)the speed of the particle.

Solution

(i) sin 30 = r/2. Therefore r = 2 sin 30 = 1 m
(ii) Force up = Force down
T cos 30 = 4g
T = (80/\3) N
(iii) Net Force Inwards =

(80/\3)(0.5) = 4v
2
/1
v = 2.4 m/s



Problems which involve a reaction force
2005 (a) [Ordinary Level]
A smooth particle of mass 4 kg is attached to the end of a light inextensible string 50 cm in length.
The mass describes a horizontal circle with constant speed 3 m/s on a smooth horizontal table.
The centre of the circle is also on the table.
(i) Show on a diagram all the forces acting on the particle.
(ii) Find the tension in the string.

Solution
(i) See diagram

(ii) T = mv
2
/r
= 4(3)
2
/0.5
T = 72 N

1. Forces up = Forces down equation 1

2.

equation 2

3. Solve both equations

6

For You
2010 (b) [Ordinary Level]
A conical pendulum consists of a particle of mass 3 kg attached by a light
inelastic string of length 1 metre to a fixed point P.
The particle describes a horizontal circle of radius r.
The centre of the circle is vertically below P.
The string makes an angle of o with the vertical where tan o = 4/3.
Find
(i) the value of r
(ii) the tension in the string
(iii)the angular velocity of the particle.


2004 (a) [Ordinary Level]
A boy ties a 1 kg mass to the end of a piece of string 50 cm in length.
He then rotates the mass on a smooth horizontal table, so that it describes a horizontal circle whose centre is
also on the table.
If the string breaks when the tension in the string exceeds 8 newtons, what is the greatest speed with which
the boy can rotate the mass?


2007 (b) [Ordinary Level]
A smooth particle of mass 2 kg is attached by a light inelastic string to a fixed point p.
The particle describes a horizontal circle of radius 0.5 m on the smooth surface of a horizontal table.
The centre of the circle is vertically below the point p.
The string makes an angle with the vertical, where tan = .
The tension in the string is 15 newtons.
Find
(i) the reaction force between the particle and the table
(ii) the angular speed of the particle.


2005 (b) [Ordinary Level]
A smooth particle, of mass 4 kg, describes a horizontal circle of radius r cm on
a smooth horizontal table with constant speed 1.2 m/s.
The particle is connected by means of a light inelastic string to a fixed point o
which is 40 cm vertically above the centre of the circle.
The length of the string is 50 cm.
(i) Find the value of r.
(ii) Find the tension in the string.
(iii)Find the normal reaction between the particle and the table.


2003 (b) [Ordinary Level]
A smooth particle, of mass 2 kg, describes a horizontal circle of radius 0.5
metres on a smooth horizontal table with constant angular velocity 3 radians
per second.
The particle is connected by means of a light inelastic string to a fixed point o
which is vertically above the centre of the circle.
The length of the string is 1 metre.
The inclination of the string to the vertical is .
(i) Find .
(ii) Find the tension in the string.
(iii)Show that the normal reaction between the particle and the table is 20 9\3 N.

7

2002 [Ordinary Level]
A particle of mass 5 kg describes a horizontal circle of radius 0.7 metres with constant angular velocity
radians per second on a smooth horizontal table.
The particle is connected by means of a light inextensible string to a fixed point o which is vertically above
the centre of the circle.
The inclination of the string to the vertical is , where tan = .
The tension in the string is T newtons, the normal reaction between the particle and the table is R newtons
and R = T\5.
(i) Write down the value of sin and the value of cos .
(ii) Show on a diagram all the forces acting on the particle.
(iii)Find the value of T and the value of R.
(iv) Find the value of .


2000 [Ordinary Level]
A particle of mass 20 kg describes a horizontal circle of radius length 12 cm with
constant angular velocity of 4 rad/s on a smooth horizontal table.
The particle is connected by means of a light inextensible string to a fixed point o
which is vertically above the centre of the circle.
The inclination of the string to the vertical is u, where tan u = 5/12.
(i) Show on a diagram all the forces acting on the particle.
(ii) Show that the value of the normal reaction between the particle and the table is
equal to the value of the tension in the string.




8

Cones and Spheres: Ordinary Level

2001 [Ordinary Level]
A smooth particle of mass 2 kg describes a horizontal circle of radius r metres with constant angular velocity
radians per second on the smooth inside surface of a hemispherical bowl of radius 0.5 metres.
The centre of the horizontal circle is
0.4 metres vertically below the centre of the circle formed by the rim of the
bowl.
The normal reaction between the particle and the bowl makes an angle with
the horizontal.
(i) Find the value of r.
(ii) Write down the value of cos and of sin.
(iii)Show on a diagram all the forces acting on the particle.
(iv) Find the normal reaction between the particle and the bowl.
(v) Find the value of .


2008 (b) [Ordinary Level]
{the marking scheme here is incorrect; they didnt convert a distance of 4 cm to 0.04 m}
A hemispherical bowl of diameter 10 cm is fixed to a horizontal surface.
A smooth particle of mass 2 kg describes a horizontal circle of radius r cm on
the smooth inside surface of the bowl.
The plane of the circular motion is 2 cm above the horizontal surface.
(i) Find the value of r.
(ii) Show on a diagram all the forces acting on the particle.
(iii)Find the reaction force between the particle and the surface of the bowl.
(iv) Calculate the angular velocity of the particle.



2009 (b) [Ordinary Level]
A right circular hollow cone is fixed to a horizontal surface.
Its semi-vertical angle is 30

and its axis is vertical.

A smooth particle of mass 2 kg describes a horizontal circle of radius r cm on the
smooth inside surface of the cone.
The plane of the circular motion is 5 cm above the horizontal surface.
(i) Find the value of r in surd form.
(ii) Show on a diagram all the forces acting on the particle.
(iii)Find the reaction force between the particle and the surface of the cone.
(iv) Calculate the angular velocity of the particle.



9

Cones and Spheres: (mostly) Higher Level

1984 (a)
A particle moving on the inside smooth surface of a fixed hollow sphere of internal radius 2 m describes a
horizontal circle of radius 1 m.
Calculate the angular velocity of the particle.


1979 (a)
A particle moving at constant speed, is describing a horizontal circle on the inside surface of a smooth
sphere of radius r.
The centre of the circle is a distance r below the centre of the sphere.
Prove that the speed of the particle is
gr 6
2
1



2004 (b) [Ordinary Level] {this one could/should be a higher level question}
A circus act uses a fixed spherical bowl of inner radius 5 m.
A girl and her motorcycle together have a mass of M kg, as shown in the diagram.
The girl and her motorcycle describe a horizontal circle of radius r m, with angular
velocity rad/s, on the inside rough surface of the bowl.
The centre of the horizontal circle is 3 m vertically below the centre of the bowl.
The coefficient of friction between the motorcycle tyres and the bowl is 3/4.
(i) Find the value of r.
(ii) Show on a diagram all the forces acting on the mass M.
(iii)Find the value of , correct to two decimal places.



1983
A hollow right circular cone of semi-vertical angle where tan = is fixed with its axis vertical and
vertex downwards.
The inner surface of the cone is rough with coefficient of friction and the cone rotates about its axis with
uniform angular velocity 7 rad/s.
A particle of mass m is placed on the inside surface and rotates with the cone at a vertical height h above the
vertex.
Calculate the normal reaction of the particle with the inside surface and the height h above the vertex if
(i) the particle is about to slide down
(ii) the particle is about to slip up.


2006 (b)
A hollow cone with its vertex downwards and its axis vertical, revolves about its axis with a
constant angular velocity of 4 rad/s.
A particle of mass m is placed on the inside rough surface of the cone.
The particle remains at rest relative to the cone.
The coefficient of friction between the particle and the cone is 1/4.

The semi-vertical angle of the cone is 30 and the particle is a distance l m from the vertex of
the cone. Find the maximum value of l, correct to two places of decimals.



10

Higher Level: Particles on a string

2008 (b)
A and B are two fixed pegs, A is 4 m vertically above B.
A mass m kg, connected to A and B by two light inextensible strings of equal length, is
describing a horizontal circle with uniform angular velocity .
For what value of will the tension in the upper string be double the tension in the lower
string?


2011 (b)
A and B are two fixed pegs.
A is 4 m vertically above B.
A mass m kg, connected to A and B by two light inextensible strings of equal length, l, is
describing a horizontal circle with uniform angular velocity .
Find the value of if the ratio of the tensions in the two strings is 11: 9.


1981 (b)
A heavy particle is describing a circle on a smooth horizontal table with uniform angular velocity e.
It is partially supported by a light inextensible string attached to a fixed point 0.1 metres above the table.
Calculate the value of W if the normal reaction of the table on the particle is half the weight of the particle.


1988
A particle of mass 8 kg is describing a circle, with constant speed v, on a smooth horizontal table.
It is connected by a light inextensible string of length 3 m to a point which is 1 m vertically above the centre
of the circle.
(i) Calculate the tension in the string.
(ii) Show that the particle will remain in contact with the table if v < g 8
(iii)If the speed of the particle is increased to g 1 . 9 , calculate the height at which the particle rotates above
the table.


1982 (a)
The diagram shows a string prq which is fixed at p and where q is vertically below p. r
is a smooth ring threaded on the string which is made to rotate at an angular velocity
rad/s in a horizontal circle centre q, the string being taut.
If |pq| = 0.12 m, |pr| + |rq| = 0.18 m, show that = 294 rad/s.


1984 (b)
Two particles of equal mass attached by a taut inextensible string of length 2y rests on a horizontal circular
table.
The particles are respectively y and 3y from the centre of the table so that centre and particles are collinear.
The table rotates about its centre with angular velocity and the coefficient of friction is
y
/
2
.
If both particles are on the point of slipping,
(i) show on a diagram, all the forces of the string/particle system
(ii) calculate .





11

1997 no.6
A particle P, of mass m, is suspended by two inextensible light
strings PA, PB, of equal length where A and B are fixed at the same
horizontal level and each string is inclined at an angle to the
horizontal.
(i) Find the tension in the string PA.
(ii) If the string PB is cut so that P starts to move in a circular path,
prove that the tension in the string PA when it makes an angle
with the horizontal is mg(3sin 2sin ).
(iii)If the tension in PA is suddenly halved when PB is cut, find the
angle .





12

Particle slides off the outside of a sphere












2012 (b)
A particle of mass m kg lies on the top of a smooth fixed sphere of radius 30 cm.
The particle is slightly displaced and slides down the sphere. The particle leaves the
sphere at B.
(i) Find the speed of the particle at B.
(ii) The horizontal distance, in metres, of the particle from the centre of the sphere t
seconds after it has left the surface of the sphere is

Find the value of k correct to two places of decimals.


2010 (a)
A particle of mass m kg lies on the top of a smooth sphere of radius 2 m.
The sphere is fixed on a horizontal table at P.
The particle is slightly displaced and slides down the sphere.
The particle leaves the sphere at B and strikes the table at Q.
Find
(i) the speed of the particle at B
(ii) the speed of the particle on striking the table at Q.



2004 (a)
A particle can move on the smooth outer surface of a fixed sphere of radius r.
The particle is released from rest on the smooth surface of the sphere at a height
4r/5

above the horizontal plane through the centre o of the sphere.
Find, in terms of r, the height above this plane at which the particle leaves the
sphere.



2003 (b)
A particle of mass m is held at a point p on the surface of a fixed smooth sphere, centre
o and radius r. op makes an angle with the upward vertical.
The particle is released from rest.
When the particle reaches an arbitrary point q, its speed is v.
oq makes an angle with the upward vertical.
(i) Show that v
2
= 2gr (cos cos ).
(ii) If cos = and if q is the point at which the particle leaves the surface, find the
value of .

2
3
1.

equation 1
2. Reaction force R is 0 at release point
3. KE + P.E. at top = K.E. + P.E. at release point equation 2
4. Solve equations (simplest way is to get v
2
from equation 1 and sub into equation 2)

13

Conservation of Energy

KE + P.E. at top = K.E. + P.E. at bottom

2007 (b)
A bead slides on a smooth fixed circular hoop, of radius r, in a vertical plane.
The bead is projected with speed \(10gr) from the highest point c.
It impinges upon and coalesces with another bead of equal mass at d.
cd is the vertical diameter of the hoop.
Show that the combined mass will not reach the point c in the subsequent motion.



1995 (b)
A particle of mass m, attached to a fixed point by a light inelastic string, describes a circle in a vertical plane.
The tension of the string when the particle is at the highest point of the orbit is T
1
and when at the lowest point it is T
2
.
Prove that T
2
= T
1
+ 6mg




Bead on a Hoop

1982 (b)
A small bead of mass m is threaded on a smooth circular wire of radius a, fixed with its plane vertical.
The bead is projected from the lowest point of the wire with speed u.
Show that the reaction between the bead and the wire, when the radius to the bead makes an angle of 60
0

with the downward vertical is
(

2
2
g
a
u
m


2002
A smooth uniform vertical hoop of radius r and mass M kg stands in a vertical
plane on a horizontal surface.
The hoop threads two small rings, each of mass m kg. The rings are released
from rest at the top of the hoop.
(i) When the two rings have each fallen through an angle of
o
on opposite
sides of the hoop, show that the normal force of reaction exerted by the
hoop on each ring is mg (3cos 2) N
where this force is taken to act in the outward direction from the centre of
the hoop.
(ii) Show that the hoop will rise from the table if .
3
2
M
m >
14

Friction Force
2003 (a) [Ordinary Level]
A vehicle of mass 1000 kg rounds a bend which is in the shape of an arc of a circle of radius 25 m. The
coefficient of friction between the tyres and the road is 0.8.
(i) Show on a diagram the three forces acting on the vehicle.
(ii) Calculate the maximum speed with which the vehicle can round the bend without slipping.
Give your answer correct to two places of decimals.


2000 (a) [Higher Level]
A particle is placed on a horizontal rotating turntable, 10 cm from the centre of rotation.
There is a coefficient of friction of 0.4 between the particle and the turntable.
If the speed of the turntable is gradually increased, at what angular speed will the particle begin to slide?





Periodic time T
2005 (a)
A conical pendulum consists of a light inelastic string [pq], fixed at the end p, with a particle attached to the
other end q
The particle moves uniformly in a horizontal circle whose centre o is vertically below p
If = h, find the period of the motion in terms of h


1995 (a)
A light string [op], of length l, is fixed at end o, and is attached at the other end p to a particle which is moving in a
horizontal circle whose centre is vertically below and distant h from o.
Prove that the period of the motion is
g
h
t 2


po
15

Answers to Ordinary Level Exam Questions
2010 (a)
(i) r = 3 m
(ii) e = 2 rad s
-1

2010 (b)
(i) r = 0.8 m
(ii) T = 50 N
(iii)e = 4.08 rad s
-1

2009 (a)
(i) e = 8 rad/s
(ii) Period = /2 s

2009 (b)
(i) r = 5/\3 cm
(ii)
(iii)R = 40 N
(iv) e = \600 rads/s

2008 (a)
(i) e = 2.5 rad/s
(ii) Force = 37.5 N

2008 (b)
(i) r = 4
(ii)
(iii)R = 100/3
(iv) = \3.33 rad/s

2007 (a)
(i) e = 2 rad/s
(ii) R = 1 m

2007 (b)
(i) R = 8 N
(ii) e = 3 rad/s

2006 (a)
(i)
(ii) v = 2.5 m s
-1
, a = 3.2 rad s
-1


2006 (b)
(i) r = 1 m
(ii) T = 80/\3 N
(iii)v = 2.4 m s
-1


2005 (a)
(i)
(ii) T = 72 N




16

2005 (b)
(i) r = 30 cm
(ii) T = 32 N
(iii) N = 14.4. N

2004 (a)
v = 2 m s
-1


2004 (b)
(i) r = 4 m
(ii)
(iii)= 0.85 rad/sec
2003 (a)
(i)
(ii) v = 14.14 m s
-1


2003 (b)
(i) = 30
0

(ii) T = 18 N
(iii)

2002
(i) sino = 1/\5, coso = 2/\5
(ii)
(iii)T = (50\5)/7 N
R = 250/7 N
(iv) e = 10/7 rad/s

2001
(i) r = 0.3 m
(ii) cos o = 0.6, sin o = 0.8
(iii)
(iv) R = 25 N
(v) e = 5 rad/s

2000
N = T = 104 N
17

Guide to answering Higher Level Exam Questions
2008 (b)
Straightforward. Ans: e = \(3g/2)

2007 (b)
Straightforward. Use conservation of energy to calculate the velocity of the top bead when it reaches the
bottom, then use conservation of momentum to calculate the velocity of the combined mass just after the
impact and then use conservation of energy again to see how high up the combined mass will go.
Ans: The combined mass will not reach the top again.

2006 (b)
This one was a little unusual, but if you approached it in the usual way you should pick up all the marks.
Get one equation for the forces vertically up equals forces vertically down. The tricky bit is to do with the
fact that you would imagine that the ball would tend to fall down, therefore friction should act up along the
surface, but in fact because the surface is at an angle, the ball would actually rise up along the surface and
therefore friction acts downwards.
I made that sound like I understood it, didnt I? Dont be fooled :)
Anyway, get a second equation for net force inwards equals mre
2
as normal and solve.
Ans: r = 0.43 m.

2005 (a)
Straightforward.
Forces up equal forces down, force in = mre
2
, and use geometry to get an expression for Tan u. Solve.
When you have e you still need to use the relationship T = 2/e to get T.
Ans: T= 2 (h/g)

2004 (a)
Straightforward. use conservation of energy to get one equation and net force inwards = mre
2
to get the
second equation. Remember R = 0 at the point where the particle leaves the sphere.
You will also need to use the line going through the centre point as your base-line because the height is
given with reference to there.
Then solve.
Ans: h = 8r/15

2003 (b)
(i) Straightforward in principle. Use conservation of energy: Total energy at q = Total energy at p, using a
line through the centre of the circle as the base-line.
(ii) Straightforward in principle. Net force acting inwards = mv
2
/r. R = 0 at point of departure.
Ans: = 63.6
0


2002
(i) Straightforward. Begin as usual with conservation of energy to get one equation, and net force acting
inwards = mv
2
/r to get the second equation.
(ii) This part was difficult to picture. At this stage the rings will have fallen below the halfway line, and the
force exerted by the hoop on the ring will still be the same as before. Now do forces up = forces down.
Forces up are N Cosu for each ring and R, but R = 0 at point of departure. This leads to an ugly quadratic
where and to solve you need to use the b +- (\b
2
4ac)/2a formula, where the bit inside the square root
must be real.
Ans: m > 3M/2.





18

2000 (a)
Tricky if you havent seen it before, but straightforward if you have (and it does come up every so often).
Get an expression for the friction force (F = R) and a separate expression for circular motion ( F = mre
2
).
Then simply equate to get e > \(4g).

1997
Full question
(i) Forces up = forces down and forces left = forces right.
Answer: T = mg/2 sin |
(ii) Circular motion; use conservation of energy.KE + PE at top = KE + PE at bottom. The trick here is to
take the base line as the horizontal line going through A. This means h1 = -l sin | and h2 = -l sin |.
The second equation in circular motion is F
c
= mv
2
/r. As usual with this equation, the tricky part is
calculating F
c
in this case it is T mg sin |, but it may require a little playing around with angles to verify
that.
(iii)Quite tricky.
First up, you must notice that when the string is cut | = |, so the equation in part (ii) reduces to T = mg sin
|.
From part (i) T = mg/2 sin |, so if this tension is halved it becomes T = ( ) mg/2 sin |. Now equate this
with the general equation T = mg sin | and solve.
Answer: | = 60
0
.
Told you it was tricky.
from xkcd