Heinemann Solutionbank: Core Maths 4 C4 Page 1 of 1

Solutionbank
Edexcel AS and A Level Modular Mathematics
Exam style paper
Exercise A, Question 1

Question:

1
Use the binomial theorem to expand , | x | < 2 , in ascending powers
(2+x) 2
of x, as far as the term in x3, giving each coefficient as a simplified
fraction. (6)
Solution:

x 2
(2+x) 2=22 1+
2
x
2 ( 2) ( 3) x 2
=2 1+ 2 2 + +
12 2


( 2) ( 3) ( 4) x 3
+ ...
123 2

3 1
=22 1 x + 4 x2 2 x3 + ...

1 x 3x2 x3
= 4 4 + 16 8 + ...

Pearson Education Ltd 2009

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 1 of 1

Solutionbank
Edexcel AS and A Level Modular Mathematics
Exam style paper
Exercise A, Question 2

Question:

The curve C has equation

x2 + 2y2 4x 6yx + 3 = 0
Find the gradient of C at the point (1, 3). (7)
Solution:

x2 + 2y2 4x 6yx + 3 = 0
Differentiate with respect to x:
dy dy
2x + 4y 4 6x dx + 6y =0
dx
At the point (1, 3), x = 1 and y = 3.
dy dy
2 + 12 4 6 dx + 18 =0
dx
dy
6 dx 20 = 0
dy 20 10
dx = 6 = 3
10
the gradient of C at (1, 3) is 3 .

Pearson Education Ltd 2009

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 1 of 1

Solutionbank
Edexcel AS and A Level Modular Mathematics
Exam style paper
Exercise A, Question 3

Question:

Use the substitution u = 5x + 3, to find an exact value for

10x
03 dx (9)
( 5x + 3 ) 3

Solution:

u = 5x + 3
du u3
dx = 5 and x = 5

10x 2 ( u 3 ) du
3
dx = 5
( 5x + 3 ) u3
2 u3
= 5 du
u3
2 u 3
= 5 du
u3 u3
2
= 5 u 2 3u 3 du
2 3
= u 1 + 2u 2
5
Change the limits: x = 0 u = 3 and x = 3 u = 18
2 1 3 1 3 5
Integral = 18 + 3 + =
5 2 182 2 32 108

Pearson Education Ltd 2009

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 1 of 2

Solutionbank
Edexcel AS and A Level Modular Mathematics
Exam style paper
Exercise A, Question 4

Question:

(a) Find the values of A and B for which

1 A B
( 2x + 1 ) ( x 2 )
2x + 1
+ x2
(3)

1
(b) Hence find ( 2x + 1 ) ( x 2 )
dx, giving your answer in the form y = ln f
(x) . (4)

(c) Hence, or otherwise, obtain the solution of

dy
2x + 1 x2 = 10y , y > 0, x > 2
dx
for which y = 1 at x = 3, giving your answer in the form y = f ( x ) . (5)
Solution:
1 A B A ( x 2 ) + B ( 2x + 1 )
(a) ( 2x + 1 ) ( x 2 ) ( 2x + 1 ) + (x2) ( 2x + 1 ) ( x 2 )

A ( x 2 ) + B ( 2x + 1 ) 1
1
Substitute x = 2, then 5B = 1 B= 5
1 5 2
Substitute x = 2, then 2A =1 A= 5

2 1

5 5
(b) Integral = 2x + 1 + x 2 dx

1 1
= ln 2x + 1 + 5 ln x 2 + C
5
1
|x2|
= ln k 5
| 2x + 1 |

(c) Separate the variables to give

dy 10 dx
y = ( 2x + 1 ) ( x 2 )

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 2 of 2

ln y = 2 ln | x 2 | 2 ln | 2x + 1 | + C
y = 1 when x = 3 C = 2 ln 7 = ln 49
|x2| 2
y = 49
| 2x + 1 |

Pearson Education Ltd 2009

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 1 of 2

Solutionbank
Edexcel AS and A Level Modular Mathematics
Exam style paper
Exercise A, Question 5

Question:

A population grows in such a way that the rate of change of the population P at
time t in days is proportional to P.

(a) Write down a differential equation relating P and t. (2)

(b) Show, by solving this equation or by differentiation, that the general solution
of this equation may be written as P = Akt, where A and k are positive
constants. (5)

Initially the population is 8 million and 7 days later it has grown to 8.5 million.

(c) Find the size of the population after a further 28 days. (5)
Solution:
dP
(a) dt P
dP
dt = mP

dP
(b) P = m dt
ln P = mt + C
P = emt + C
= Aemt where A = eC
= Akt where k = em

(c) When t = 0, P = 8 A=8

When t = 7, P = 8.5 8.5 = 8k7
8.5
k7 = 8
When t = 35,
P = 8k35
= 8 ( k7 ) 5

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 2 of 2

8.5 5
=8
8
= 10.8 million (to 3 s.f.)
Pearson Education Ltd 2009

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 1 of 2

Solutionbank
Edexcel AS and A Level Modular Mathematics
Exam style paper
Exercise A, Question 6

Question:

Referred to an origin O the points A and B have position vectors i 5j 7k and

10i + 10j + 5k respectively. P is a point on the line AB.

(a) Find a vector equation for the line passing through A and B. (3)

(b) Find the position vector of point P such that OP is perpendicular to

AB. (5)

(c) Find the area of triangle OAB. (4)

(d) Find the ratio in which P divides the line AB. (2)
Solution:

(a) AB = 9i + 15j + 12k (or BA = 9i 15j 12k)

the line may be written
1 9 10 3
r= 5 + 15 or r= 10 + 5 or equivalent
7 12 5 4

3 +1+9
(b) 5 . 5 + 15 = 0
4 7 + 12
+ 3 + 27 25 + 75 28 + 48 = 0
150 50 = 0
1
= 3

4
the point P has position vector 0
3

(c) | OP | = 5 and | AB | = \ 92 + 152 + 122 = 15 2

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 2 of 2

1 1 1
Area of OAB = 2 base height = 2 15 2 5 = 2 75 2

4 1 3 10 4
(d) AP = 0 5 = 5 and PB = 10 0
3 7 4 5 3
6
= 10
8
PB = 2AP
i.e. P divides AB in the ratio 1 : 2.
Pearson Education Ltd 2009

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 1 of 3

Solutionbank
Edexcel AS and A Level Modular Mathematics
Exam style paper
Exercise A, Question 7

Question:

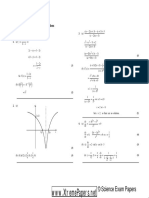
The curve C, shown has parametric equations

x = 1 3 cos t, y = 3t 2 sin 2t, 0 < t < .

(a) Find the gradient of the curve at the point P where t = 6
. (4)

(b) Show that the area of the finite region beneath the curve, between the lines
1
x= 2
, x = 1 and the x-axis, shown shaded in the diagram, is given by the
integral

2 9t sin t dt 2 12 sin2 t cos t dt. (4)
3 3

(c) Hence, by integration, find an exact value for this area. (7)

Solution:

(a) x = 1 3 cos t, y = 3t 2 sin 2t

dx dy
dt = 3 sin t and dt = 3 4 cos 2t
dy 3 4 cos 2t
dx = 3 sin t

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 2 of 3

dy 32 2
When t = 6 , dx = = 3
3
( )
2

dx
(b) The area shown is given by t t2y dt dt
1
1
Where t1 is value of parameter when x = 2
and t2 is value of parameter when x = 1
1
i.e. 1 3 cos t1 = 2
1
cos t1 = 2

t1 = 3
Also 1 3 cos t2 = 1
cos t2 = 0

t2 = 2
The area is given by


2 3t 2 sin 2t 3 sin t dt
3

= 2 9t sin t dt 2 6 2 sin t cos t sin t dt Using the double
3 3

angle formula

= 2 9t sin t dt 2 12 sin2 t cos t dt
3 3

(c) Area = [ 9t cos t ] 2 + 2 9 cos t dt [ 4 sin3 t ] 3
3 3 2

= [ 9t cos t + 9 sin t 4 sin3 t] 2
3

3 93 33
= 94 2 + 2 4 8

3
=533+ 2

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013

Heinemann Solutionbank: Core Maths 4 C4 Page 3 of 3

Pearson Education Ltd 2009

file://C:\Users\Buba\Desktop\further\Core Mathematics 4\content\sb\content\c4_mex2_a... 3/6/2013