11 Physics Imp ch14 Marks 4
11 Physics Imp ch14 Marks 4
Uploaded by
Parijat Deb RoyCopyright:
Available Formats
11 Physics Imp ch14 Marks 4
11 Physics Imp ch14 Marks 4
Uploaded by
Parijat Deb RoyOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Copyright:
Available Formats
11 Physics Imp ch14 Marks 4
11 Physics Imp ch14 Marks 4
Uploaded by
Parijat Deb RoyCopyright:
Available Formats
CBSE
Class 11 physics
Important Questions
Chapter 14
Oscillations
4 Marks Questions
1. Which of the following examples represent (nearly) simple harmonic motion and
which represent periodic but not simple harmonic motion?
(a) the rotation of earth about its axis.
(b) motion of an oscillating mercury column in a U-tube.
(c) motion of a ball bearing inside a smooth curved bowl, when released from a point
slightly above the lower most point.
(d) general vibrations of a polyatomic molecule about its equilibrium position.
Ans.(b) and (c) are SHMs
(a) and (d) are periodic, but not SHMs
(a) During its rotation about its axis, earth comes to the same position again and again in
equal intervals of time. Hence, it is a periodic motion. However, this motion is not simple
harmonic. This is because earth does not have a to and fro motion about its axis.
(b) An oscillating mercury column in a U-tube is simple harmonic. This is because the
mercury moves to and fro on the same path, about the fixed position, with a certain period of
time.
(c) The ball moves to and fro about the lowermost point of the bowl when released. Also, the
ball comes back to its initial position in the same period of time, again and again. Hence, its
motion is periodic as well as simple harmonic.
(d) A polyatomic molecule has many natural frequencies of oscillation. Its vibration is the
superposition of individual simple harmonic motions of a number of different molecules.
Material downloaded from myCBSEguide.com. 1 / 11
Hence, it is not simple harmonic, but periodic.
2. Which of the following functions of time represent (a) simple harmonic, (b) periodic
but not simple harmonic, and (c) non-periodic motion? Give period for each case of
periodic motion ( is any positive constant):
(a)
(b)
(c) 3 cos (π/4 - 2 t)
(d) cos t + cos 3 t + cos 5 t
(e) exp
(f) 1 + t +
Ans.(a) SHM
The given function is:
This function represents SHM as it can be written in the form:
Its period is:
Material downloaded from myCBSEguide.com. 2 / 11
(b) Periodic, but not SHM
The given function is:
3. A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20
cm. A body suspended from this balance, when displaced and released, oscillates with a
period of 0.6 s. What is the weight of the body?
Ans. Maximum mass that the scale can read, M = 50 kg
Maximum displacement of the spring = Length of the scale, l = 20 cm = 0.2 m
Time period, T = 0.6 s
Maximum force exerted on the spring, F = Mg
Where,
g = acceleration due to gravity = 9.8 m/
F = 50 9.8 = 490
∴Spring constant,
Mass m, is suspended from the balance.
Time period,
∴Weight of the body = mg = 22.36 9.8 = 219.167 N
Hence, the weight of the body is about 219 N.
Material downloaded from myCBSEguide.com. 3 / 11
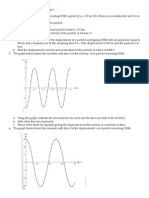
4. Figures 14.29 correspond to two circular motions. The radius of the circle, the period
of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-
clockwise) are indicated on each figure.
Obtain the corresponding simple harmonic motions of the x-projection of the radius
vector of the revolving particle P, in each case.
Ans.(a) Time period, T = 2 s
Amplitude, A = 3 cm
At time, t = 0, the radius vector OP makes an angle with the positive x-axis, i.e., phase
angle
Therefore, the equation of simple harmonic motion for thex-projection of OP, at time t, is
given by the displacement equation:
(b) Time period, T = 4 s
Amplitude, a = 2 m
Material downloaded from myCBSEguide.com. 4 / 11
At time t = 0, OP makes an angle π with the x-axis, in the anticlockwise direction. Hence,
phase angle, Φ = + π
Therefore, the equation of simple harmonic motion for the x-projection of OP, at time t, is
given as:
5. Cylindrical piece of cork of density of base area A and height h floats in a liquid of
density . The cork is depressed slightly and then released. Show that the cork
oscillates up and down simple harmonically with a period
Where is the density of cork. (Ignore damping due to viscosity of the liquid).
Ans.Base area of the cork = A
Height of the cork = h
Density of the liquid =
Density of the cork =
In equilibrium:
Weight of the cork = Weight of the liquid displaced by the floating cork
Let the cork be depressed slightly by x. As a result, some extra water of a certain volume is
displaced. Hence, an extra up-thrust acts upward and provides the restoring force to the
cork.
Up-thrust = Restoring force, F = Weight of the extra water displaced
Material downloaded from myCBSEguide.com. 5 / 11
F = –(Volume Density g)
Volume = Area Distance through which the cork is depressed
Volume = Ax
∴ F = – A g … (i)
According to the force law:
F = kx
Where, k is a constant
…….(ii)
The time period of the oscillations of the cork:
……….(iii)
Where,
m = Mass of the cork
= Volume of the cork Density
= Base area of the cork Height of the cork Density of the cork
= Ah
Hence, the expression for the time period becomes:
Material downloaded from myCBSEguide.com. 6 / 11
6. A mass attached to a spring is free to oscillate, with angular velocity , in a
horizontal plane without friction or damping. It is pulled to a distance x0and pushed
towards the centre with a velocity v0at time t = 0. Determine the amplitude of the
resulting oscillations in terms of the parameters Ô°, x0and v0. [Hint: Start with the
equation x = a cos ( ) and note that the initial velocity is negative.]
Ans.The displacement equation for an oscillating mass is given by:
x=
Where,
A is the amplitude
X is the displacement
θ is the phase constant
Velocity,
At t= 0,
… (i)
And,
… (ii)
Squaring and adding equations (i) and (ii), we get:
Material downloaded from myCBSEguide.com. 7 / 11
Hence, the amplitude of the resulting oscillation is .
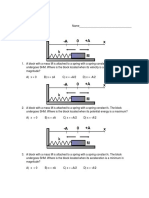
7. A spring having with a spring constant 1200 N is mounted on a horizontal table
as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then
pulled sideways to a distance of 2.0 cm and released.
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and
(iii) the maximum speed of the mass.
Ans.Spring constant, k = 1200 N
Mass, m = 3 kg
Displacement, A = 2.0 cm = 0.02 cm
(i) Frequency of oscillation v, is given by the relation:
Where, T is the time period
Hence, the frequency of oscillations is 3.18 cycles per second.
(ii) Maximum acceleration (a) is given by the relation:
a =
Material downloaded from myCBSEguide.com. 8 / 11
Where,
= Angular frequency =
A = Maximum displacement
Hence, the maximum acceleration of the mass is 8.0 .
(iii) Maximum velocity,
Hence, the maximum velocity of the mass is 0.4 m/s.
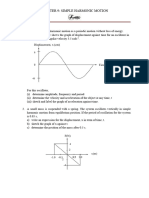
8. Answer the following questions:
(a) Time period of a particle in SHM depends on the force constant k and mass m of the
particle:
. A simple pendulum executes SHM approximately. Why then is the time
period of a pendulum independent of the mass of the pendulum?
(b) The motion of a simple pendulum is approximately simple harmonic for small angle
oscillations. For larger angles of oscillation, a more involved analysis shows that T is
greater than . Think of a qualitative argument to appreciate this result.
(c) A man with a wristwatch on his hand falls from the top of a tower. Does the watch
give correct time during the free fall?
(d) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is
Material downloaded from myCBSEguide.com. 9 / 11
freely falling under gravity?
Ans.(a) The time period of a simple pendulum,
For a simple pendulum, k is expressed in terms of mass m, as:
k m
= Constant
Hence, the time period T, of a simple pendulum is independent of the mass of the bob.
(b) In the case of a simple pendulum, the restoring force acting on the bob of the pendulum
is given as:
F = –mg sinθ
Where,
F = Restoring force
m = Mass of the bob
g = Acceleration due to gravity
θ = Angle of displacement
For small θ, sinθ
For large θ, sinθ is greater than θ.
This decreases the effective value of g.
Hence, the time period increases as:
T=
Material downloaded from myCBSEguide.com. 10 / 11
Where, l is the length of the simple pendulum
(c) The time shown by the wristwatch of a man falling from the top of a tower is not affected
by the fall. Since a wristwatch does not work on the principle of a simple pendulum, it is not
affected by the acceleration due to gravity during free fall. Its working depends on spring
action.
(d) When a simple pendulum mounted in a cabin falls freely under gravity, its acceleration is
zero. Hence the frequency of oscillation of this simple pendulum is zero.
Material downloaded from myCBSEguide.com. 11 / 11
You might also like
- PSI AP Physics 1: Simple Harmonic Motion Practice ProblemsDocument18 pagesPSI AP Physics 1: Simple Harmonic Motion Practice Problemsaman100% (1)
- Grade 12 Physics - Energy, Work, and PowerDocument28 pagesGrade 12 Physics - Energy, Work, and PowerJabez CabahugNo ratings yet
- Magnetic Field of A Current Carrying CoilDocument9 pagesMagnetic Field of A Current Carrying CoilShayan AliNo ratings yet
- Group Work 3 For S5 MPC and MPGDocument8 pagesGroup Work 3 For S5 MPC and MPGdaniel.kamanzi1343No ratings yet
- Simple Harmonic MotionDocument7 pagesSimple Harmonic MotionRaju SinghNo ratings yet
- Exercises August 14, 2019Document3 pagesExercises August 14, 2019Lester Patalinghug BernardinoNo ratings yet
- Home Assignment I PHY 105/PHY 2105 PhysicsDocument1 pageHome Assignment I PHY 105/PHY 2105 PhysicsMd. Imran AhmedNo ratings yet
- Tutorial 10 Oscillations - 2024Document2 pagesTutorial 10 Oscillations - 2024Niza SikanyikaNo ratings yet
- Advanced Higher Mechanics Tutorial 6Document2 pagesAdvanced Higher Mechanics Tutorial 6veluarasuNo ratings yet
- Sheets PDFDocument6 pagesSheets PDFmayank singhNo ratings yet
- Oscillations TheoryDocument10 pagesOscillations TheoryJoanna PanayiNo ratings yet
- 11 Ws Ch 14 Oscillations Qp 2023-24Document4 pages11 Ws Ch 14 Oscillations Qp 2023-24aarav28mNo ratings yet
- 11 Physics Imp Ch14 Marks 5Document23 pages11 Physics Imp Ch14 Marks 5Akshanth NNo ratings yet
- Simple Harmonic MotionDocument7 pagesSimple Harmonic MotionRaju SinghNo ratings yet
- SHM SubjectiveDocument8 pagesSHM SubjectiveAtulNo ratings yet
- (83463) 14. AH Simple Harmonic Motion QuestionsDocument12 pages(83463) 14. AH Simple Harmonic Motion QuestionsCiaraNo ratings yet
- SHM WSDocument3 pagesSHM WSTrishnee MunusamiNo ratings yet
- KuizDocument3 pagesKuizokky ardNo ratings yet
- Chapter 14 SlidesDocument40 pagesChapter 14 SlidessuperwebonNo ratings yet
- 12 5 2018 15 32 58 119 QBank PH1103 EnggPhysicsDocument11 pages12 5 2018 15 32 58 119 QBank PH1103 EnggPhysicsRNo ratings yet
- Practice Hookes and SHM SolutionsDocument10 pagesPractice Hookes and SHM SolutionsZhong Huang100% (2)
- Tutorial Waves and OscillationDocument3 pagesTutorial Waves and OscillationVardhan MunglaNo ratings yet
- Physics Half YearlyDocument12 pagesPhysics Half YearlyNaman Poswal Class 9DNo ratings yet
- Bansal Simple Harmonic MotionDocument24 pagesBansal Simple Harmonic Motionbhnprtp90No ratings yet
- A2 RevisionDocument10 pagesA2 Revisiongaya8404No ratings yet
- AL Physics/S.H.M./P.1: DX DT BXDocument4 pagesAL Physics/S.H.M./P.1: DX DT BXmiguelNo ratings yet
- 11 Physics Imp Ch14 Marks 3Document12 pages11 Physics Imp Ch14 Marks 3Akshanth NNo ratings yet
- SHM and Waves Problem SetDocument5 pagesSHM and Waves Problem SetbananacrunchNo ratings yet
- Simple Harmonic Motion Problems With Answers FINALDocument15 pagesSimple Harmonic Motion Problems With Answers FINALAngel100% (2)
- Periodic Motion 2Document4 pagesPeriodic Motion 2Tilak NeupaneNo ratings yet
- Soalan KumBe Topik 9 SHMDocument3 pagesSoalan KumBe Topik 9 SHMnurfarahanii06No ratings yet
- Physics Question Bank L-1 3 Oscillation XIDocument2 pagesPhysics Question Bank L-1 3 Oscillation XIhappypateljayesh20061410No ratings yet
- Physics I Problems PDFDocument1 pagePhysics I Problems PDFbosschellenNo ratings yet
- Simple Harmonic Motion Worksheet 3: X (T) (7.8 CM) Cos (T)Document3 pagesSimple Harmonic Motion Worksheet 3: X (T) (7.8 CM) Cos (T)NadeenMohamedNo ratings yet
- Annual Examination Physics (Theory) Code - B: Time: 3 Hours Max. Marks: 70Document4 pagesAnnual Examination Physics (Theory) Code - B: Time: 3 Hours Max. Marks: 70Sumathi SrinivasNo ratings yet
- SHM ReviewDocument2 pagesSHM ReviewShabbir H. KhanNo ratings yet
- New Life Christian High School: Name: - COMBDocument4 pagesNew Life Christian High School: Name: - COMBjian mne jNo ratings yet
- SHM Ex1Document2 pagesSHM Ex1Kshitij BansalNo ratings yet
- Sample Paper Physics Class XiDocument6 pagesSample Paper Physics Class XiBhaskar JhaNo ratings yet
- PCS125 Tutorial QuestionsDocument52 pagesPCS125 Tutorial Questionsfurbac321No ratings yet
- Worksheet - RevisionDocument7 pagesWorksheet - RevisionAliza IsmailNo ratings yet
- Physics Practice ProblemDocument1 pagePhysics Practice ProblemnurulalomadorNo ratings yet
- Ap Physics C - Homework 8, Oscillations: AnswersDocument1 pageAp Physics C - Homework 8, Oscillations: AnswersRegina LinNo ratings yet
- Problems On The Osillatory MotionDocument4 pagesProblems On The Osillatory MotionAhmed RashadNo ratings yet
- 3765-Books-Doubtnut-Question-Bank NBNNBNBNBDocument117 pages3765-Books-Doubtnut-Question-Bank NBNNBNBNBAriana GuillenNo ratings yet
- Problems 15 Serway 6 eDocument16 pagesProblems 15 Serway 6 eAndre CVNo ratings yet
- MP112 Mechanics and Modern Physics Problem Set 6 / 2015Document2 pagesMP112 Mechanics and Modern Physics Problem Set 6 / 2015CristianNo ratings yet
- 11 Physics Imp ch14 NumericalsDocument4 pages11 Physics Imp ch14 NumericalsAkshanth NNo ratings yet
- 11 Physics Oscillations and Waves Test 01Document1 page11 Physics Oscillations and Waves Test 01Edukondalu NamepalliNo ratings yet
- Physics I Problems PDFDocument1 pagePhysics I Problems PDFBOSS BOSSNo ratings yet
- Chapter 15 Electric FieldsDocument17 pagesChapter 15 Electric FieldsdrewNo ratings yet
- SheetDocument3 pagesSheetAly ElbarodyNo ratings yet
- Physics 295 Oscillation ProblemsDocument3 pagesPhysics 295 Oscillation ProblemsDennisIgoyDacanayNo ratings yet
- Physics 295 Oscillation ProblemsDocument3 pagesPhysics 295 Oscillation ProblemsDennisIgoyDacanayNo ratings yet
- Practice Test For Midterm 3 Chapters 13, 15, 16, 17, 18 in Preparation For The Midterm ExamDocument11 pagesPractice Test For Midterm 3 Chapters 13, 15, 16, 17, 18 in Preparation For The Midterm ExamRAIZZNo ratings yet
- I-Taalem Task - Chapter 8Document3 pagesI-Taalem Task - Chapter 8ruzaimi98No ratings yet
- Physics I Problems PDFDocument1 pagePhysics I Problems PDFBOSS BOSSNo ratings yet
- MCQ OscillationsDocument3 pagesMCQ OscillationsYoussef HassanNo ratings yet
- SHM - Wave - Sound Practice KeyDocument19 pagesSHM - Wave - Sound Practice KeyanirudhNo ratings yet
- Explain Quantum Physics With a Single-Particle in Motion: Anharmonic OscillatorFrom EverandExplain Quantum Physics With a Single-Particle in Motion: Anharmonic OscillatorNo ratings yet
- Mathematics Preboard Exam 16 - Math 6Document10 pagesMathematics Preboard Exam 16 - Math 6Raymond L. Dela Costa33% (3)
- A Presentation On: ResistojetDocument14 pagesA Presentation On: ResistojetudhayNo ratings yet
- Astrophysics Research Paper TopicsDocument8 pagesAstrophysics Research Paper TopicsafmcsvatcNo ratings yet
- RFT 043 RFT 072: Return Filters - LightlineDocument5 pagesRFT 043 RFT 072: Return Filters - LightlineYazad DoctorrNo ratings yet
- Design of A 30K Single-Stage Free-Piston Stirling CryocoolerDocument8 pagesDesign of A 30K Single-Stage Free-Piston Stirling Cryocoolerpooriya zamaniNo ratings yet
- Accredited Laboratory: The American Association For Laboratory AccreditationDocument6 pagesAccredited Laboratory: The American Association For Laboratory AccreditationWaqar YounasNo ratings yet
- TimeHistoryAnalysis SzymanskiDocument41 pagesTimeHistoryAnalysis Szymanskiseljak_veseljakNo ratings yet
- SPE-185861-MS Pressure Transient Analysis in Advanced Wells Completed With Flow Control DevicesDocument20 pagesSPE-185861-MS Pressure Transient Analysis in Advanced Wells Completed With Flow Control DevicesM.No ratings yet
- HESCO Intreviews March 2023Document14 pagesHESCO Intreviews March 2023Usama FarooqNo ratings yet
- 01 Semiconductor TheoryDocument32 pages01 Semiconductor TheoryAnmay MishraNo ratings yet
- Sand Replacement TestDocument8 pagesSand Replacement Testkrishna buildconNo ratings yet
- Lecture 1Document68 pagesLecture 1Ama Serwaa YeboahNo ratings yet
- Table Des Primitives UsuellesDocument1 pageTable Des Primitives UsuellesCRYPTEXNo ratings yet
- PS1800 Pool CS 37 1Document2 pagesPS1800 Pool CS 37 1Prim AristaNo ratings yet
- EC3-D13 Alco controller για digital scrollDocument2 pagesEC3-D13 Alco controller για digital scrollLefti YMNo ratings yet
- Fred W. Price - The Planet Observer's Handbook-Cambridge University Press (2000)Document225 pagesFred W. Price - The Planet Observer's Handbook-Cambridge University Press (2000)Xtet Aung100% (1)
- Manual SKF TMEH 1 Analisador de AceiteDocument64 pagesManual SKF TMEH 1 Analisador de Aceitemanuel muñozNo ratings yet
- SRM501E Final ExamDocument3 pagesSRM501E Final ExammargaridaNo ratings yet
- 16ECEE - Fajfar PeterDocument62 pages16ECEE - Fajfar PeterHaluk SesigürNo ratings yet
- PHYS 121 - Curriculum - HuyDocument4 pagesPHYS 121 - Curriculum - HuyHuong TruongNo ratings yet
- Master of Science (M.SC.) (Physics) Semester-IV (C.B.S.) Examination Solid State Physics-Ii Compulsory Paper-1Document2 pagesMaster of Science (M.SC.) (Physics) Semester-IV (C.B.S.) Examination Solid State Physics-Ii Compulsory Paper-1Sanyam KumariNo ratings yet
- SRPNSAFETY VehicleAccessDocument5 pagesSRPNSAFETY VehicleAccessJNo ratings yet
- Transformation 4 HelpDocument3 pagesTransformation 4 HelpMc LovinNo ratings yet
- ProductOverview 2023 EN-38Document1 pageProductOverview 2023 EN-38Ismail AliNo ratings yet
- Superman - The MovieDocument138 pagesSuperman - The MovieEduardo Teixeira VieiraNo ratings yet
- WEEK 2 (Feb 8 - 13) :: REAL-TIME LIVE SESSION - Video Recording Must Be Uploaded/posted To Google ClassroomDocument12 pagesWEEK 2 (Feb 8 - 13) :: REAL-TIME LIVE SESSION - Video Recording Must Be Uploaded/posted To Google ClassroomJoshua John JulioNo ratings yet
- Microscopy) Microscope - Basics and BeyondDocument50 pagesMicroscopy) Microscope - Basics and BeyondpcelkamajaNo ratings yet
- Intelligent Routines II - Solving Linear Algebra and Differential Geometry With SageDocument319 pagesIntelligent Routines II - Solving Linear Algebra and Differential Geometry With SageNuno Neves100% (3)