Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd Logo
Upload

Welcome to Scribd!

  • 8 views

    MAT 136 CH 5 Theorem

    Uploaded by

    Chilli Lee
    1) The document summarizes several tests used to determine if a series converges or diverges, including the divergence test, geometric series test, p-series test, comparison test, limit comparison test, integral test, alternating series test, ratio test, and root test. 2) Each test lists the conclusions about convergence or divergence based on the limiting behavior or properties of the series terms. 3) Additional comments provide context or limitations for each test.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd

    MAT 136 CH 5 Theorem

    Uploaded by

    Chilli Lee
    8 views3 pages
    1) The document summarizes several tests used to determine if a series converges or diverges, including the divergence test, geometric series test, p-series test, comparison test, limit comparison test, integral test, alternating series test, ratio test, and root test. 2) Each test lists the conclusions about convergence or divergence based on the limiting behavior or properties of the series terms. 3) Additional comments provide context or limitations for each test.

    Original Title

    MAT 136 Ch 5 theorem

    Copyright

    © © All Rights Reserved

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    1) The document summarizes several tests used to determine if a series converges or diverges, including the divergence test, geometric series test, p-series test, comparison test, limit comparison test, integral test, alternating series test, ratio test, and root test. 2) Each test lists the conclusions about convergence or divergence based on the limiting behavior or properties of the series terms. 3) Additional comments provide context or limitations for each test.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    8 views3 pages

    MAT 136 CH 5 Theorem

    Uploaded by

    Chilli Lee
    1) The document summarizes several tests used to determine if a series converges or diverges, including the divergence test, geometric series test, p-series test, comparison test, limit comparison test, integral test, alternating series test, ratio test, and root test. 2) Each test lists the conclusions about convergence or divergence based on the limiting behavior or properties of the series terms. 3) Additional comments provide context or limitations for each test.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    of 3

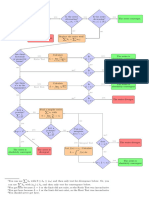
    Chapter 5 | Sequences and Series 517

    Series or Test Conclusions Comments

    Divergence Test If n lim


    →∞ n
    a = 0, the test This test cannot prove convergence
    ∞ of a series.
    For any series ∑ a n, evaluate is inconclusive.
    n=1
    lim a .
    n→∞ n If n lim
    →∞ n
    a ≠ 0, the
    series diverges.

    Geometric Series If |r| < 1, the series Any geometric series can be
    ∞ reindexed to be written in the form
    ∑ ar n − 1 converges to
    a/(1 − r). a + ar + ar 2 + ⋯, where a is the
    n=1
    initial term and r is the ratio.

    If |r| ≥ 1, the series


    diverges.

    p-Series If p > 1, the series For p = 1, we have the harmonic


    ∞
    ∞
    ∑ 1
    np
    converges.
    series ∑ 1/n.
    n=1
    n=1
    If p ≤ 1, the series
    diverges.

    Comparison Test If a n ≤ b n for all n ≥ N Typically used for a series similar to


    ∞ ∞ a geometric or p -series. It can
    For ∑ a n with nonnegative and ∑ b n converges,
    n=1 sometimes be difficult to find an
    n=1
    appropriate series.
    terms, compare with a known ∞
    ∞
    then ∑ a n converges.
    series ∑ b n. n=1
    n=1

    If a n ≥ b n for all n ≥ N
    ∞
    and ∑ b n diverges,
    n=1
    ∞
    then ∑ a n diverges.
    n=1

    Limit Comparison Test If L is a real number and Typically used for a series similar to
    ∞ ∞ a geometric or p -series. Often
    For ∑ a n with positive terms, L ≠ 0, then ∑ an
    n=1 easier to apply than the comparison
    n=1
    ∞ ∞ test.
    compare with a series ∑ bn and ∑ b n both
    n=1 n=1
    by evaluating converge or both diverge.
    an
    L = n lim
    → ∞bn
    .

    Table 5.3 Summary of Convergence Tests


    518 Chapter 5 | Sequences and Series

    Series or Test Conclusions Comments

    ∞
    If L = 0 and ∑ bn
    n=1
    ∞
    converges, then ∑ an
    n=1
    converges.

    ∞
    If L = ∞ and ∑ bn
    n=1
    ∞
    diverges, then ∑ an
    n=1
    diverges.

    Integral Test ∞ ∞ Limited to those series for which the


    If there exists a positive, ∫ f (x)dx and ∑ an corresponding function f can be
    N n=1
    continuous, decreasing function easily integrated.
    f such that a n = f (n) for all both converge or both
    ∞ diverge.
    n ≥ N, evaluate ∫ f (x)dx.
    N

    Alternating Series If b n + 1 ≤ b n for all Only applies to alternating series.


    ∞ ∞
    ∑ (−1) n + 1 b n or ∑ (−1) n b n n ≥ 1 and b n → 0, then
    n=1 n=1 the series converges.

    Ratio Test If 0 ≤ ρ < 1, the series Often used for series involving
    ∞ factorials or exponentials.
    For any series ∑ a n with converges absolutely.
    n=1
    nonzero terms, let If ρ > 1 or ρ = ∞, the
    ρ = n lim
    | |
    an + 1
    → ∞ an
    . series diverges.

    If ρ = 1, the test is
    inconclusive.

    Root Test If 0 ≤ ρ < 1, the series Often used for series where

    For any series ∑


    ∞
    a n, let converges absolutely. |a n| = b nn.
    n=1
    n
    ρ= lim a .
    n → ∞ | n| If ρ > 1 or ρ = ∞, the
    series diverges.

    Table 5.3 Summary of Convergence Tests

    This OpenStax book is available for free at http://cnx.org/content/col11965/1.2


    Chapter 5 | Sequences and Series 519

    Series or Test Conclusions Comments

    If ρ = 1, the test is
    inconclusive.

    Table 5.3 Summary of Convergence Tests

    You might also like