Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.

com

Computer Science

Grade: XI

Number system and conversion Boolean

logic

Reference Note

Unit Wise Important Questions for Computer Science XI

Unit 2 Number System and Conversion Boolean Logic
1) What is a number system? What are the types of number systems used in a computer?
2) What is the difference between positional and non-positional number systems?
3) Define radix/base of a number system. What is the radix for binary, octal, decimal and hexadecimal number
system?
4) What is a binary number system? Why is it used in computer systems?
5) What is hexadecimal number system?
6) What is Boolean algebra? Give its applications.
7) What is Boolean logic? Explain the three Boolean operators with the help of truth table.
8) What is a truth table? Differentiate between NAND and NOR gate with truth table.
9) What is a logic gate? Construct truth table, logic diagram, Venn diagram of AND, OR and NOT gates.
10) Prove de-Morgan's law with truth table.
11) What is a Boolean law? Explain the different laws of Boolean algebra.
12) State and verify the associative and distributive laws of Boolean algebra.
13) Subtract 10001 from 11011 using 1's and 2's complement method.
14) Convert the following as indicated.
a) (AF9)16=(?)2 b) (100101)2=(?)16 c) (129)16=(?)8 d) (2EA)16= (?)10
15) Write Short notes on: a) Principle of Duality? b) Use of Boolean algebra

Website: www.bkbhusal.com.np 1 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

Unit 2 Number System and Conversion Boolean Logic

Computer Number System

The number system plays a vital role in computer calculations. Number system is an organized and
systematic way of representing numbers. Number systems are basically of two types: non-positional and
positional number systems.

1. Non-Positional Number System

The non-positional number system is a number system in which each symbol represents the same value,
regardless of its position in the number. The symbols are simply added to find out the value of a particular
number. The most common non-positional number system is the Roman Number System. It is a system
of representing numbers devised by the ancient Romans. It is based on certain letters which are given
values as numerals.

2. Positional Number System

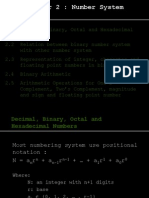
Positional number system can be represented by a few symbols called digits, which represent different
values depending on the position that they occupy. The value of each digit in such a number is determined
by the digits itself, the position of the digit in the number, and by the base of the number system. The
main positional number systems used in computer are decimal, binary, octal and hexadecimal.

Different types of number system are as follows:

a. Decimal number system: A number system having base or radix 10 is called decimal number
system.
Examples: (789)10 or (789)D
b. Binary number system: A number system having base or radix 2 is called binary number system.
Examples: (110)2
c. Octal number system: A number system having base or radix 6 is called octal number system.
Examples: (1234)8
d. Hexadecimal number system: A number system having base or radix 16 is called hexadecimal
number system. Examples: (C01F)16 or (C01F)H

1. Decimal Number System

The base or radix of a number system is the number of different symbols available to represent any digit
within that system. For example, the decimal system (Base 10) has a radix of 10. Decimal uses different
combinations of 10 symbols to represent any value (i.e. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9).

2. Binary Number System

A number system having base or radix 2 is called binary number system. It consists of 2 bits: 0 and 1. It is
also known as Binary digits. It is specially used in internal processing of computer system.
An electronic circuit has two states either ON state or OFF state. The bit 1 represents the high voltage i.e.
ON state and the bit 0 represents the low voltage i.e. OFF state of an electronic circuit. So it is used in
computer system.

3. Octal Number System

A number system having base or radix 8 is called octal number system. It consists of 8 digits: 0, 1, 2, 3, 4,
5, 6, 7). It is also known as octonary number system. The octal system is used in computing as a simple
means of expressing binary quantities.

Website: www.bkbhusal.com.np 2 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

4. Hexa- Decimal Number System

A number system having base or radix 16 is called hexadecimal number system. It consists of 16 digits: 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F. It is also used in computer basically in memory management.

Number Conversion:
Rules
1. Decimal Number System to Others (Binary, Octal, Hexa-Decimal) Number System = Divide (2,8,16)
2. Others (Binary, Octal, Hexa-Decimal) Number System to Decimal Number System= Multiply (2,8,16)
3. Binary Number system to Octal Number system and Vice versa = 3 bit binary Grouping Method (421)
4. Binary Number System to Hexa-Decimal Number System and Vice versa= 4 bit binary Grouping Method ( 8421)
5. Octal Number System to Hexa-decimal Number System and Vice versa= 3 bit & 4 bit groping Method (421 & 8421)

Number Conversion: Rules in short

1 Decimal N.S.(10) To Others N.S.(2,8,16) = Divide (2,8,16)

2 Others N.S. (2,8,16) To Decimal N.S.(10) = Multiply (2,8,16) x

3 3 bit binary grouping method (421) Octal (8)

Binary (2)

4 bit binary grouping method (8421) Hexa- Decimal (16)

Number Conversion examples

a. Decimal to Binary
Here, (149)10
2 149 1
2 74 0
2 37 1
2 18 0
2 9 1
2 4 0
2 2 0
2 1 1
0

Therefore, (149)10 = (10010101)2

Website: www.bkbhusal.com.np 3 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

b. Decimal to Octal
Here, (804)10
8 804 4
8 100 4
8 12 4
8 1 1
0

Therefore, (804)10 = (1444)8

c. Decimal to Hexa- decimal

Here, (1600)10
16 1600 0
16 100 4
16 6 6
0

Therefore, (1600)10 = (640)16

d. Binary to Decimal
Here, (100100)2 = 25 x 1 + 24 x 0 + 23 x 0 + 22 x 1 + 21 x 0 + 20 x 0
= 32 + 0 + 0 + 4 + 0 + 0
= (36)10

e. Octal to Decimal
Here, (2040)8 = 83 x 2 + 82 x 0 + 81 x 4 + 80 x 0
= 1024 + 32
= (1056)10

f. Hexa-decimal to Decimal
Here, (1E0D)16 = 163 x 1 + 162 x E + 161 x 0 + 160 x D
= 4096 + 256 x 14 + 0 + 1 x 13
= 4096 + 3584 + 13
= (7693)10

g. Binary to Octal
Here, (110111101)2
110 111 101 (: 3 bit binary grouping method

6 7 5

Therefore, (110111101)2 = (675)8

Website: www.bkbhusal.com.np 4 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

h. Binary to Hexa-decimal
Here, (1001110111)2
0010 0111 0111
2 7 7

Therefore, (1001110111)2 = (277)16

i. Octal to Binary
Here, (375)8
3 7 5
011 111 101

Therefore, (375)8 = (11111101)2

j. Hexa-decimal to Binary
Here, (ABC)16
A B C
1010 1011 1100

Therefore, (ABC)16 = (101010111100)2

k. Octal to Hexa-decimal
Here, (555)8
5 5 5
101 101 101

= (101101101)2
0001 0110 1101
1 6 D

Therefore, (555)8 = (16D)16

l. Hexa-decimal to Octal
Here, (BCA)16
B C A
1011 1100 1010
= (101111001010)16
101 111 001 010
5 7 1 2

Therefore, (BCA)16 = (5712)8

Website: www.bkbhusal.com.np 5 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

Fractional Number System Conversion

a. Decimal to Binary
Here, (0.55)10
0.55 x 2 = 1.1 1
0.1 x 2 = 0.2 0
0.2 x 2 = 0.4 0
0.4 x 2 = 0.8 0
0.8 x 2 = 1.6 1
0.6 x 2 = 1.2 1
Therefore, (0.55)10 = (0.100011)2
b. Decimal to Octal
Here, (234.997)10
8 234 2
8 29 5
8 3 3
0
Also
0.997 x 8 = 7.976 7
0.976 x 8 = 7.808 7
0.808 x 8 = 6.464 6
0.464 x 8 = 3.712 3
0.712 x 8 = 5.696 5
0.696 x 8 = 5.568 5
Therefore, (234.997)10 = (352.776355)2

c. Decimal to Hexa-decimal
Here, (689.336)10
16 689 1
16 43 11 = B
16 2 2
0
Also
0.336 x 16 = 5.376 5
0.376 x 16 = 6.016 6
0.016 x 16 = 0.256 0
0.256 x 16 = 4.096 4
0.096 x 16 = 1.536 1
0.536 x 16 = 8.576 8
Therefore, (689.336)10 = (2B1.560418)16

Website: www.bkbhusal.com.np 6 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

d. Binary to Decimal
Here, (101.1101)2 = 22 x 1 + 21 x 0 + 20 x 1 + 2-1 x 1 + 2-2 x 1 + 2-3 x 0 + 2-4 x 1
= 4 + 0 + 1 + 0.5 + 0.25 + 0 + 0.0625
= (5.8125)10

e. Octal to Decimal
Here, (0.1042)8 = 8-1 x 1 + 8-2 x 0 + 8-3 x 4 + 8-4 x 2
= 0.125 + 0 + 0.0078125 + 0.00048828125
= (0.1333)10

f. Hexa-decimal to Decimal
Here, (FA.AEF)16 = 161 x 15 + 160 x 10 + 16-1 x 10 + 16-2 x 14 + 16-3 x 15
= 240 + 10 + 0.625 + 0.0546875 + 0.00366211
= 250.68335

g. Binary to Octal
Here, (101010.110111)2
101 010 110 111
5 2 6 7
Therefore, (101010.110111)2 = (52.67)8

h. Binary to Hexa-decimal
Here, (10101.11011)2
0001 0101 1101 1000
1 5 D 8
Therefore, (10101.11011)2 = (15.D8)16

i. Octal to Binary
Here, (77.226)8
7 7 2 2 6
111 111 010 010 110
Therefore, (77.226)8 = (111111.010010110)2

j. Octal to Hexa-decimal
Here, (0.376)8
3 7 6
011 111 110
= (011111110)2
0111 1111
7 F

Therefore, (0.376)8 = (0.7F)16

Website: www.bkbhusal.com.np 7 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

k. Hexa-decimal to Binary
Here, (0.5AB)16
5 A B
0101 1010 1011
Therefore, (0.5AB)16 = (0.010110101011)2

l. Hexa-decimal to Octal
Here, (0.226)16
2 2 6
0010 0010 0110
= (0.001000100110)2
001 000 100 110
1 0 4 6
Therefore, (0.226)16 = (0.1046)8

Binary Arithmetic
a. Binary Addition
Here, 11111 + 10001 Rule for addition
11111 0+0=0
+ 10001 0+1=1
110000 1+0=1
1+1=10 (0 with carry over 1)
1+1+1=11 (1 with carry over 1)
1+1+1+1=100 (0 with carry over 10)
Here, 1111 + 1111 1+1+1+1+1=101 (0 with carry over 10)
1111
+ 1111
11110
b. Binary Subtraction
Here, 1100 - 11
1100
- 0011
1001
Rule for Subtraction
Here, 101010 - 1001 0-0=0
101010 1-0=1
- 001001 1-1=0
100001 0-1=1 (with borrowing 1 from left side
Then it becomes 10 i.e. 10-1=1)

c. Binary Multiplication
Here, 1010 x 1010
1010
x 1010 Rule for Multiplication
0x0=0
0000
1x0=0
1010x
0x1=0
0000xx 1x1=1
1010xxx
1100100

Website: www.bkbhusal.com.np 8 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

Here, 1111 x 1111

1111
x 1111
1111
1111x
1111xx
1111xxx
11100001

d. Binary Division
Here, 110100 / 110
110) 110100 (1000
Rule for Division
110
1÷1=1
________ 0÷1=0
100 1÷0= not defined
000 0÷0= not defined
_______
100
Therefore, Quotient = 1000 and Remainder = 100

Here, 11010001 / 1001

1001) 11010001 (10111
1001
________
1000
0000
_______
10000
01001
_______
1110
1001
_____
1011
1001
______
10
Therefore, Quotient = 10111 and Remainder = 10

1's and 2's Binary Subtraction Method

A compliment is process of representing the negative numbers or bits in digital computer system.
Complements are used in digital computers for simplifying the subtraction operation and for logical
manipulation. Using complements, all the arithmetic operators can be performed in the form of addition.
The process of subtraction using 2's complement is given below:
a. Make the number of digits equal in both minuend and subtrahend.
b. Calculate 2's complement of subtrahend.
c. Calculate sum of minuend and 2's complement of subtrahend.
d. Check the overflow digit (carry).
e. If there is overflow digit, discard it and the remaining bits would be final answer.
f. If there is no overflow bit then the result must be negative. So again, calculate 2's complement of
the sum and that would be the final answer.

Website: www.bkbhusal.com.np 9 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

1'S AND 2'S COMPLEMENT BINARY SUBTRACTION METHOD

1. Subtract 110 from 1101 using 1's complement binary subtraction method.
Using 1's complement method:
Here Main value= 1101
Second Value= 110
i. Make the number of bits equal as 1101 and 0110.
ii. 1's complement of second value 0110 is 1001.
iii. Add both the bits:
1101
+ 1001
1 0110
Here, we got overflow bit so discard it and add the remaining part.
0110 + 1 = 0111
Thus, 1101 - 110 = 111
Using 2's complement method:
Here Main value= 1101
Second Value= 110
i. Make the number of bits equal as 1101 and 0110.
ii. 1's complement of second value 0110 is 1001.
iii. 2's Complement of 1001 + 1 = 1010.
iv. Add both numbers:
1101
+ 1010
1 0111
Here, we got overflow bit which is discarded and the remaining part is our answer.
Thus, 1101 - 110 = 111

2. Subtract 1111 from 1100 using 1's and 2's complement binary subtraction method.
Here, Main value =1100
Second value= 1111
Both are equal digit.
Using 1's complement method:
i. 1's complement of second value 1111 is 0000.
ii. Add both the bits:
1100
+ 0000
1100
Here, we did not get overflow bit so we again calculate 1's complement of 1100 i.e. 0011 and put
minus sign before it.
Thus, 1100 - 1111 = -11

Using 2's complement method:

i. 1's complement of second value 1111 is 0000.
ii. 2's complement of 0000 + 1 = 0001.
iii. Add both numbers:
1100
+ 0001
1101
Here, we did not get overflow bit so, we again calculate 2's complement of 1101 and put minus
sign before it.
i.e. 0010 + 1 =0011
Thus, 1101 - 110 = -11
Website: www.bkbhusal.com.np 10 YouTube Channel:www.youtube.com/BkBhusalEduZone
 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

9'S AND 10'S COMPLEMENT DECIMAL SUBTRACTION METHOD

1. Subtract 123 from 1234 using 9's and 10's decimal subtraction method.
Using 9's complement method:
Main value=1234
Second value=123
i. Making the numbers equal in both minuend and subtrahend as 1234 and 0123.
ii. 9's complement of 0123 is (9999-0123) = 9876.
iii. Adding both numbers:
1234
+ 9876
1 1110
Here, we got overflow digit, so we discard it and add it to the remaining part.
Thus, 1110 + 1 = 1111
Using 10's complement method:
Main value=1234
Second value=123
i. Making the numbers equal in both minuend and subtrahend as 1234 and 0123.
ii. 9's complement of 0123 is (9999-0123) = 9876.
iii. 10's complement of 0123 is (9876+1) = 9877.
iv. Adding both numbers:
1234
+ 9877
1 1111
Here, we got overflow digit, so we discard it and remaining will the answer.
Thus, 1234 - 123 = 1111
2. Subtract 4567 from 567 using 9's and 10's decimal subtraction method.
Using 9's complement method:
Main value= 567
Second value= 4567
Using 9's complement method:
i. Making the numbers equal in both minuend and subtrahend as 0567 and 4567.
ii. 9's complement of 4567 (9999-4567) is 5432.
iii. Adding both numbers:
0567
+ 5432
5999
Here, we did not get overflow digit, so we again calculate 9's complement of it.
i.e. 9999-5999 becomes 4000
Thus, 567 - 4567 = 4000
Using 10's complement method:
i. Making the numbers equal in both minuend and subtrahend as 0567 and 4567.
ii. 9's complement of 4567 (9999-4567) is 5432.
iii. 10's complement of 4567 (5432+1) is 5433.
iv. Adding both numbers:
0567
+ 5433
6000
Here, we did not get overflow digit, so we again calculate 10's complement of it.
i.e. (9999-6000)= 3999 + 1 = 4000
Thus, 567 - 4567 = 4000

Website: www.bkbhusal.com.np 11 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

Boolean algebra
Boolean algebra:
Boolean algebra is a study of mathematical operations performed on certain variables (called binary
variables) that can have only two values: true (represented by 1) or false (represented by 0).

Logic Function (Boolean Function):

A logic function is an expression algebraically with binary variables, logical operation symbols, parenthesis
and equal sign, is known as Boolean function. Example, F= A.B.C'+A.B

Truth Table:
Truth table is a table which represents all the possible values of logical variables/statements along with
all the possible results of the given combinations of values. For example, following logical statements can
have only one of the two values (TRUE (YES) or FALSE (NO)).
Logic gates:
Logic gates perform basic logical functions and are the fundamental building blocks of digital integrated
circuits. Most logic gates take an input of two binary values, and output a single value of a 1 or 0.

1. AND Gate: AND gate generates true output if all the inputs are true, otherwise it generates false
output. It is denoted by (.) operator and graphically represented by:
Logical Symbol

Truth Table
Input Output
A B F=A.B
0 0 0
0 1 0
1 0 0
1 1 1

2. OR Gate: OR gate generates true if at least any one of the input is true, otherwise it generates false
Output. It is denoted by (+) operator and graphically represented by:
Logical Symbol

Truth Table
Input Output
A B F=A+B
0 0 0
0 1 1
1 0 1
1 1 1

Website: www.bkbhusal.com.np 12 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

3. NOT Gate: It is also known as inverter. It inverts the input state from true to false and vice versa. It
is denoted by (_) or (') operator and graphically represented by:
Logical Symbol

Truth Table
Input Output
A F=A'
0 1
1 0

4. NAND Gate: NAND gate is the combination of AND and NOT gate. NAND gate generates true (1) output
if at least any of the input is false otherwise, it generates false output. Graphically it is represented by:
Logical Symbol

Truth table
Input Output

A B A.B F=(A.B)'

0 0 0 1

0 1 0 1

1 0 0 1

1 1 1 0

5. NOR Gate: NOR gate is the combination of the OR gate and NOT gate. This electronic gate produces
True (1) output when all inputs are False (0) otherwise the output will be False (0). It is the complement
of the OR gate. It has two or more inputs and only one output.

Logical Symbol:
The truth-table of NOR gate is:
Input Output

A B (A+B) F=(A+B)'

0 0 0 1

0 1 1 0

1 0 1 0

1 1 1 0

Website: www.bkbhusal.com.np 13 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

6. Exclusive (X-OR)Gates:
The XOR gate produces false output (0) when both the inputs are same otherwise, the output will be
true (1). It can also have two or more inputs which produces only one output.
Logical Symbol:

The truth table of X-OR gate is given below:

Inputs Output

A B A' B' A'.B A.B' F=A'.B+A.B'

0 0 1 1 0 0 0

0 1 1 0 1 0 1

1 0 0 1 0 1 1

1 1 0 0 0 0 0

7. Exclusive-NOR(X-NOR) Gate:
The XNOR (exclusive-NOR) gate is a combination XOR gate followed by an inverter. Its output is "true" if
the inputs are the same and output is "false" if the inputs are different.
The X-NOR gate symbol is given below:

The truth table of X-NOR gate is given below:

Input Output

A B A' B' A'.B' A.B F=A.B+A'.B'

0 0 1 1 1 0 1

0 1 1 0 0 0 0

1 0 0 1 0 0 0

1 1 0 0 0 1 1

Website: www.bkbhusal.com.np 14 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

There are 2 De Morgan's laws or theorems:

a. Theorem 1: The complement of a sum of variables is equal to the product of the complement of
each variables.
(A+B)' = A'.B'

A B A' B' A+B (A+B)' A'.B'

0 0 1 1 0 1 1
0 1 1 0 1 0 0
1 0 0 1 1 0 0
1 1 0 0 1 0 0

Here, (A+B)' = A'.B' thus proved.

b. Theorem 2: The complement of a product of variables is equal to the sum of the complement of
each variables.
(A.B)' = A' + B'

A B A' B' A.B (A.B)' A'+B'

0 0 1 1 0 1 1
0 1 1 0 0 1 1
1 0 0 1 0 1 1
1 1 0 0 1 0 0

Here, (A.B)' = A' + B' thus proved.

Duality principle:
Duality principle state can be obtained by replacing AND (.) with OR (+) and vice versa, 1 with 0 and vice
versa keeping variables and complements and variables are unchanged.
For example, duality of the expression A.B' = A+B' and A'.B+C = A'+B.C

Laws of Boolean algebra

The Boolean laws are the rules for manipulating Boolean variables by using Boolean operations. This set
of rules states that how variables and values assigned with the Boolean operators reacts. These laws are
used to circuit minimization. The process of shorting the length and using minimum components to
construct same functioning circuit is called circuit minimization. The Boolean laws are as follows.

7.
a.
Here, A.(B +C) = A+(B.C)

b.
Here, A.B + C.1 + 0.1 = A + B.C + 0.1 + 0

Website: www.bkbhusal.com.np 15 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

c.
Here, C.D + A.0 + 1 = C + D.A + 1.0

d.
Here, 1.0 + A + C.1 = 0 + 1.A.C + 0

8.
Associative law states that when ORing or ANDing more than two variables, the result is the same
regardless of the grouping of the variables.
(a) (A + B) + C = A + (B + C)
(b) (A B) C = A (B C)
Proof:
A B C A+B B+C (A+B)+C A+(B+C)
0 0 0 0 0 0 0
0 0 1 0 1 1 1
0 1 0 1 1 1 1
0 1 1 1 1 1 1
1 0 0 1 0 1 1
1 0 1 1 1 1 1
1 1 0 1 1 1 1
1 1 1 1 1 1 1
Here, (A + B) + C = A + (B + C) thus proved.

Distributive law states that ORing/ANDing two or more variables and then ANDing/ORing the result with
a single variable is equivalent to ANDing/ORing the single variable with each of the two or more variables
and then ORing/ANDing the products/sums.
(a) A (B + C) = A.B + A . C
(b) A + (B . C) = (A + B) . (A + C)
Proof:
A B C B+C A.B A.C A.(B+C) A.B+A.C
0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 0 0 0 0
1 0 0 1 0 0 0 0
1 0 1 1 0 1 1 1
1 1 0 1 1 0 1 1
1 1 1 1 1 1 1 1

Here, A.(B+C) = A.B + A.C thus proved.

Website: www.bkbhusal.com.np 16 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

9.
a.
Here,
AB + A'BC + BC
= AB + BC(A'+1)
=AB + BC
=B(A + C)

The truth table is:

A B C A+C B(A+C)
0 0 0 0 0
0 0 1 1 0
0 1 0 0 0
0 1 1 1 1
1 0 0 1 0
1 0 1 1 0
1 1 0 1 1
1 1 1 1 1

b.
Here,
PQ' + Q(P + Q) + P(P' + Q)
= PQ' + PQ + QQ + PP' + PQ
= PQ' + PQ + Q + 0
= P(Q'+Q) + Q
=P+Q

The truth table is:

P Q P+Q
0 0 0
0 1 1
1 0 1

Website: www.bkbhusal.com.np 17 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

1 1 1

c.
Here,
(X + Y)(XY'Z + XYZ + XY'Z')
= XY'Z + XYZ + XY'Z' + XYY'Z + XYZ + XYY'Z'
= XY'Z + XYZ + XY'Z' + 0 + 0
=XY' (Z + Z') + XYZ
= XY' + XYZ
= X(Y'+YZ)
= X(Y'+ Z)

The truth table is:

X Y Z Y' Y'+Z X(Y'+Z)
0 0 0 1 1 0
0 0 1 1 1 0
0 1 0 0 0 0
0 1 1 0 1 1
1 0 0 1 1 1
1 0 1 1 1 1
1 1 0 0 0 0
1 1 1 0 1 1

10.
Here,
a = A.B.C
b = A' + B + C
c = A'.B'.C

Now, a + b + c = A.B.C + A'+ B + C + A'.B'.C

= B + A' + C + A'B'C
= A' + B' + C

Website: www.bkbhusal.com.np 18 YouTube Channel:www.youtube.com/BkBhusalEduZone

 Computer Science Reference Note for Grade-XI E-mail ID: bkbhusalinfo@gmail.com

Principle of duality

 Changing to symbol OR (+) operation from AND (.) operation or AND (.) operation from OR (+)
operation and digits 0 and 1 that is called principle of duality.
 Example, (x+y).z=(x.y)+z

Uses of gates

 All the gates are used to design digital electronic circuit.

 XOR and XNOR gates are used for circuit minimization.
 The NAND and NOR gates are used for construction of flash memory. Flash memories are used in
various devices like PDA, Laptops, mobiles phones etc.
 Flash memory are constructed by using NOR are gates and external memories constructor by using
NAND gates. For example, mini SD, Micro SD, Memory Cards.

Uses of Boolean algebra in computer science

 Logical function are useful not only to the hardware designer in implementing circuits but also to
software designer in making decision, performing arithmetic, recognizing characters and patterns,
checking for errors, formatting output and assembling and disassembling data.

Website: www.bkbhusal.com.np 19 YouTube Channel:www.youtube.com/BkBhusalEduZone