Volumeno

Konuso, sfero kaj cilindro de radiuso r kaj alto h

La volumeno estas la spaco okupata de iu korpo.

Francisko Azorín havigas la saman difinon de volumeno nome Spaco okupata de korpo. Li indikas etimologion el la latina volumen (volumeno). Kaj li aldonas la terminon volumenmetro, por aparato por mezuri volumenojn de korpoj; kaj volumenmetrio.

La formulsignalo jenas  V. La SI-unuo estas  m³ (kubmetro).

Historio

La unuaj konataj formuloj de la volumenkalkulo devenas el Egiptio. La Moskva papiruso estas kolektaĵo de kalkuloj kaj datita al la jaro 1850 a.K.. Interalie aperas tie la formuloj por kalkuli la volumenon de egalflanka kvarangula konuso.

La kalkulo okazis per analizo kaj konekta sintezo. Tio signifas, ke la korpoj estis al konataj korpoj diserigitaj kaj la unuopaj volumenoj estis adiciitaj.

Mezurmetodoj

Dum longa tempo evoluis multaj metodoj por mezuri, kalkuli la volumenon:

• Plenigo: La korpo estis per sablo aŭ akvo plenigita, kies kvanto estis difinita per konata barelo.
• Akvoelpremo La korpo estas mergata en barelon plenigitan tute per akvo. La superfluita akvo estas mezurita en konata barelo.

Algebra kalkulo

Oni povas el konataj dimensioj kaj formoj kalkuli la volumenon de korpo, por kiu estis priskribita matematika formulo:

$\operatorname {Vol} (D)=\iiint \limits _{D}dx\,dy\,dz$

Tiel volumeno de regiono D estas triopa integralo de la konstanta funkcio 1 tra la regiono.

Ekzemploj:

• Kubo kun longo de latero a:
  $V=a\cdot a\cdot a=a^{3}$
• Pilko kun radiuso r:
  $V={{4} \over {3}}\pi r^{3}$
• Rotacianta korpo de funkcio f(x) ĉe rotacio ĉirkaŭ x-akso:
  $V=\pi \cdot \int _{a}^{b}(f(x))^{2}\mathrm {d} x$

Kelkaj formuloj por elementaraj solidoj

Formo	formulo de volumeno	Variabloj
Kubo	$V=a^{3}\;$
Briko	$V=abc$
Prismo (B: areo de bazo)	$V=Bh$
Piramido (B: areo de bazo)	$V={\frac {1}{3}}Bh$
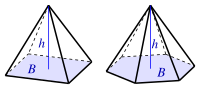
Parallelepipedo	$V=abc{\sqrt {K}}$ ${\begin{aligned}K=1&+2\cos(\alpha )\cos(\beta )\cos(\gamma )\\&-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )\end{aligned}}$
Regula kvaredro (tetrahedrono)	$V={{\sqrt {2}} \over 12}a^{3}\,$
Sfero	$V={\frac {4}{3}}\pi r^{3}$
Ellipsoido	$V={\frac {4}{3}}\pi abc$
Cirkula Cilindero	$V=\pi r^{2}h$
Konuso	$V={\frac {1}{3}}\pi r^{2}h$
Solida toro	$V=2\pi ^{2}Rr^{2}$
Solido de revolucio	$V=\pi \cdot \int _{a}^{b}f(x)^{2}\mathrm {d} x$
Solida korpo kun kontinua areo $A(x)$ de ĝiaj sekcoj (examplo: Steinmetz solid)	$V=\int _{a}^{b}A(x)\mathrm {d} x$	Por la supra solido de revolucio: $A(x)=\pi f(x)^{2}$

Mezurunuoj

1 m³= 1000 dm³ = 1000 Litroj

forstoekonomio:
1 spacometro (staploligno) = 0.7 m³ (lignomaso sen interna aero)

Vidu ankaŭ

• Longo, larĝo, profundo, alto
• Areo
• Volumena integralo