楕円体・回転楕円体の意味と体積・表面積
高校数学で習う楕円: の三次元バージョンを考えます。
-
で表される曲面を楕円面と言う。 -
楕円面を表面とする立体
を楕円体と言う。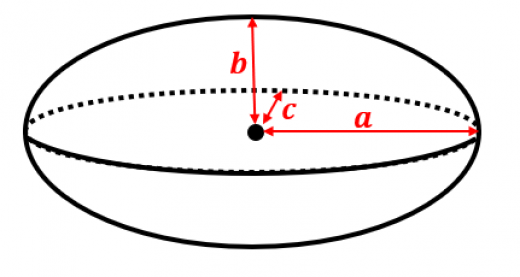
-
特に, のうち2つ以上が等しい場合,楕円面のことを回転楕円面と言い,楕円体のことを回転楕円体と言う。
-
の場合は球面・球になる。
この記事では とします。
回転楕円体の特徴
回転楕円体の特徴
回転楕円体は,その名の通り,楕円を回転させてできる立体です。
2次元平面上の楕円を,その長軸または短軸に関して回転させてできる立体は回転楕円体。
を 軸のまわりに回転させた立体 を考える( 軸まわりの回転も同様)。

が に含まれる
と の距離が 以下
これは,回転楕円体の式。
回転楕円体では「仲間外れの係数の変数が回転軸」になります。例えば,上記の場合, で仲間外れは であり,回転軸は 軸です。
楕円体の体積
楕円体の体積
次は体積です。体積は簡単です。
楕円体: の体積は,
- 回転楕円体の体積も,この定理から計算できます。
- の場合は,球の体積公式 になります。
- 楕円の面積公式 と似ています。
証明は「楕円体を拡大・縮小して球にする」ことで簡単にできます。拡大・縮小については 関数のグラフの拡大・縮小の証明と例 を参照ください。
楕円体 を 軸方向に 倍に拡大し, 軸方向に 倍に拡大すると,
になる。 これは半径 の球であるので,体積は
よって,拡大前の楕円体の体積は
長楕円体と扁平楕円体
長楕円体と扁平楕円体
回転楕円体には2種類あります。
-
長楕円体(長球):回転軸が別の軸よりも長い。つまり,回転楕円体の式 において, の場合。ボールの北極と南極をつかんで引き伸ばすイメージ。ラグビーボール。
-
扁平楕円体(扁球):回転軸が別の軸よりも短い。つまり,回転楕円体の式 において, の場合。ボールの北極と南極から押しつぶすイメージ。地球は球に近い扁平楕円体とみなすことが多い。 のことを扁平率と呼ぶことがある。
回転楕円体の表面積
回転楕円体の表面積
表面積の公式は,長球と扁球で異なります!
回転楕円体:
の表面積 は,
- のとき
- のとき
ただし,,は離心率です。→離心率の意味と関連する計算
長球のときはサインの逆関数,扁球のときは の逆関数が出てくるのがおもしろいです!→ 双曲線関数(sinhx, coshx, tanhx)の逆関数
 から の間にある部分の表面積を考える。この部分は が十分小さいとき「長さが で太さが の帯」とみなせるので,表面積は
から の間にある部分の表面積を考える。この部分は が十分小さいとき「長さが で太さが の帯」とみなせるので,表面積は
よって,積分すると
まず,被積分関数を で表す。
- より
- また,これを で微分すると
以上より,
ここで, の場合,上式は
と置換すると,
ただし, と,
より
の場合も同様に計算できる。
楕円面の媒介変数表示
楕円面の媒介変数表示
楕円面 は,媒介変数 (ただし,)を用いて以下のように表せます: これは,球面の媒介変数表示(→ここの公式5)を知っていればすぐに導出できます。
一般の楕円体の表面積は計算が大変です。楕円積分が登場します。











