正多面体が5種類しかないことの2通りの証明
正多面体は,正4面体,正6面体,正8面体,正12面体,正20面体の5つのみ。
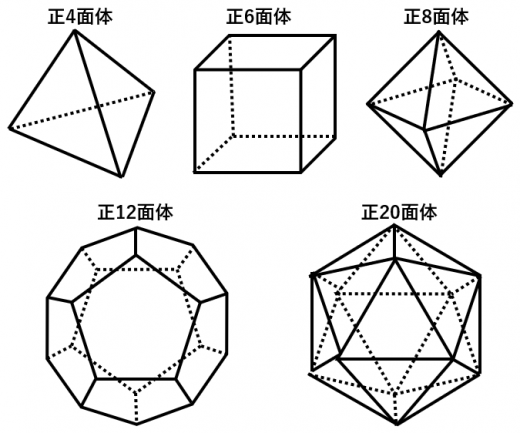
正多面体とは何かを説明したあと,正多面体がこの5種類しかない理由を2通り紹介します。雑学として知っておくとよいでしょう。
正多面体とは
正多面体とは
そもそも「正多面体」とは何なのかきちんと確認しておきます。
以下の3つの条件を満たす多面体を正多面体と言う。
- すべての面が合同な正多角形
- どの頂点に集まる面の数も同じ
- へこんでいない(凸である)
正多面体は,とても対称性の高い立体です。
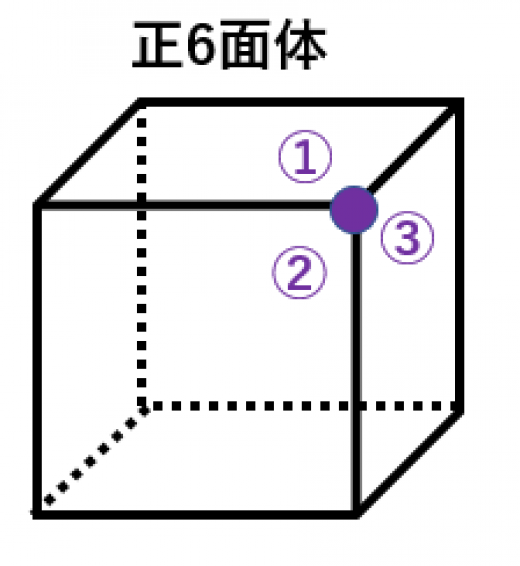 立方体(サイコロ)は正多面体です。実際,
立方体(サイコロ)は正多面体です。実際,
- すべての面が同じサイズの正方形(正四角形)
- どの頂点にも3つの面があつまる
- へこんでいない
ことがわかります。面の数が6つなので正6面体と呼ばれます。
正多面体が5種類しかないことの証明1
正多面体が5種類しかないことの証明1
1つ1つていねいに考えれば,正多面体が5種類しかないことがわかります。理由はとても単純で一つの点に集まる角度の和が 以上になることはないからです。
まず,正三角形によってつくられる正多面体を考える。
- 1つの頂点に3つの正三角形が集まる場合→正4面体
- 1つの頂点に4つの正三角形が集まる場合→正8面体
- 1つの頂点に5つの正三角形が集まる場合→正20面体
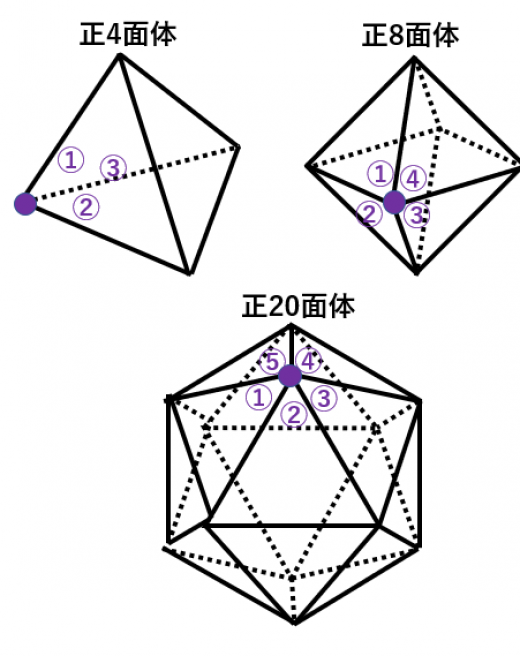
- 1つの頂点に6つ以上の正三角形が集まる場合→多面体にならない。なぜなら,一つの点に集まる角度の和が 以上になるとへこんでいない立体を作ることはできないから。
次に,正四角形によってつくられる正多面体を考える。
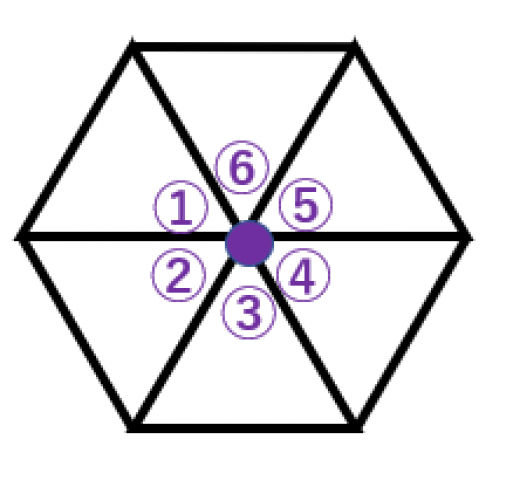
- 1つの頂点に3つの正四角形が集まる場合→正6面体

- 1つの頂点に4つ以上の正四角形が集まる場合→一つの点に集まる角度の和が 以上になるので無理。
次に,正五角形によってつくられる正多面体を考える。
- 1つの頂点に3つの正五角形が集まる場合→正12面体
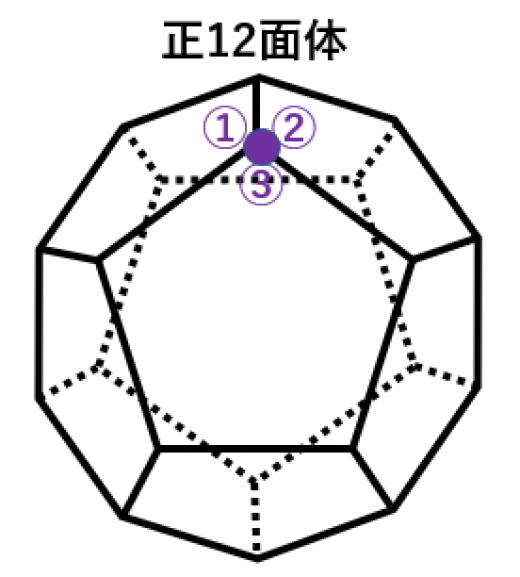
- 1つの頂点に4つ以上の正五角形が集まる場合→一つの点に集まる角度の和が 以上になるので無理。
さらに,正六角形以上によって作られる正多面体は無い。なぜなら,正六角形以上は3つ集めるだけで一つの点に集まる角度の和が 以上になるから。
赤文字の部分に納得できない人は,実際に紙などで 以上の角度を一つの頂点にへこませないように集める実験をしてみてください。
正多面体が5種類しかないことの証明2
正多面体が5種類しかないことの証明2
次は,オイラーの多面体定理というおもしろい定理を使った証明です。一般に多面体の頂点の数を ,辺の数を ,面の数を とおくと が成立します。→オイラーの多面体定理の意味と証明
個の正 角形では合わせて辺が 本あるが,一つの辺は二つの面に属するので,
また, 個の頂点にそれぞれ 本の辺が集まり,一つの辺は二つの頂点を結ぶので,
これらを に代入して のみの式にする:
右辺は正なので左辺も正。よって
これを満たす を列挙すると,
となり5種類しかないことがわかる。
辺と面と頂点の数の関係を使うのは重要な考え方です。受験や数学オリンピックに役立つかもしれません。
正多面体でないもの
正多面体でないもの
正多面体の定義
- すべての面が合同な正多角形
- どの頂点に集まる面の数も同じ
- へこんでいない(凸である)
において,条件1と3は満たすが2を満たさない例を紹介します。

図のような正三角形六個で構成される多面体を考えましょう。青の頂点からは辺が4本,緑の頂点からは辺が3本出ており条件2を満たしません。これでは「正多面体」と呼ぶには対称性が足りません。
幼少時代,正多面体のおもちゃと戯れていた過去があります。











