Euler and Hamiltonian paths are fundamental concepts in graph theory, a branch of mathematics that studies the properties and applications of graphs. An Euler path visits every edge of a graph exactly once, while a Hamiltonian path visits every vertex exactly once. These paths have significant applications in various fields, including computer science, engineering, and operations research.
Euler Paths and Circuits
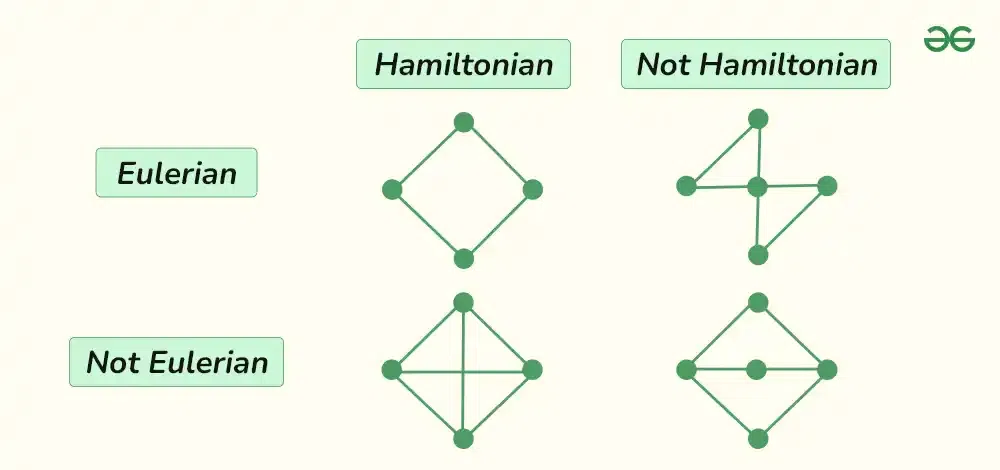
- An Euler path is a path that uses every edge of a graph exactly once.
- An Euler circuit is a circuit that uses every edge of a graph exactly once.
- An Euler path starts and ends at different vertices.
- An Euler circuit starts and ends at the same vertex.
The Konigsberg bridge problem’s graphical representation :
Conditions for Euler Paths and Circuits
- Euler Path: A connected graph has an Euler path if and only if it has exactly zero or two vertices of odd degree.
- Euler Circuit: A connected graph has an Euler circuit if and only if every vertex has an even degree.
Hamiltonian Paths
- Hamiltonian Path: A path in a graph that visits every vertex exactly once.
Unlike Euler paths, there is no simple necessary sufficient condition for the existence of Hamiltonian paths and cycles. However, there are several theorems and heuristics:
- Dirac’s Theorem: If a graph GGG has n vertices (with n≥3n \geq 3n≥3) and every vertex has a degree of at least n/2n/2n/2, then G has a Hamiltonian cycle.
- Ore’s Theorem: If a graph GGG has n vertices and for every pair of non-adjacent vertices u and v, the sum of their degrees is at least n, then G has a Hamiltonian cycle.
Hamiltonian Circuit
A simple circuit in a graph [Tex]G [/Tex]that passes through every vertex exactly once is called a Hamiltonian circuit. Unlike Euler paths and circuits, there are no simple necessary and sufficient criteria to determine if there are any Hamiltonian paths or circuits in a graph. But there are certain criteria that rule out the existence of a Hamiltonian circuit in a graph, such as if there is a vertex of degree one in a graph then it is impossible for it to have a Hamiltonian circuit.
There are certain theorems which give sufficient but not necessary conditions for the existence of Hamiltonian graphs.
Euler and Hamiltonian Paths – Solved Examples
1. Determine if the following graph has an Euler circuit:
A graph with vertices {A, B, C, D} and edges {AB, BC, CD, DA, AC}
A: To have an Euler circuit, all vertices must have even degree.
Degrees: A(3), B(2), C(3), D(2)
Since all vertices have even degree, this graph has an Euler circuit.
One possible circuit: A-B-C-D-A-C-A
2. Does the following graph have an Euler path?
A graph with vertices {P, Q, R, S} and edges {PQ, QR, RS, SP, PR}
A: For an Euler path, either all vertices have even degree, or exactly two vertices have odd degree.
Degrees: P(3), Q(2), R(3), S(2)
This graph has an Euler path (but not a circuit) because it has exactly two odd-degree vertices.
One possible path: P-S-R-Q-P-R
3. Determine if the following graph has a Hamiltonian cycle:
A complete graph K5 with 5 vertices
A: A complete graph Kn always has a Hamiltonian cycle for n ≥ 3.
So yes, K5 has a Hamiltonian cycle.
One possible cycle: 1-2-3-4-5-1
4. Does the following graph have a Hamiltonian path?
A graph with vertices {A, B, C, D, E} and edges {AB, BC, CD, DE, AE, AC}
A: This graph does have a Hamiltonian path.
One such path is: A-B-C-D-E
5. Given a graph G with 5 vertices, each of degree 4, determine if it has:
a) An Euler circuit
b) A Hamiltonian cycle
A: a) Yes, it has an Euler circuit because all vertices have even degree.
b) Yes, it has a Hamiltonian cycle. This is a complete graph K5, which always has a Hamiltonian cycle.
6. Does the complete bipartite graph K3,3 have:
a) An Euler circuit
b) A Hamiltonian cycle
A: a) No Euler circuit. All vertices have odd degree (3).
b) Yes, it has a Hamiltonian cycle. One possible cycle: 1-a-2-b-3-c-1 (where 1,2,3 are in one partition and a,b,c are in the other)
7. Consider the Petersen graph. Does it have:
a) An Euler circuit
b) A Hamiltonian cycle
A: a) No Euler circuit. All vertices have degree 3 (odd).
b) No Hamiltonian cycle. The Petersen graph is a well-known example of a 3-regular graph without a Hamiltonian cycle.
8. How many edges need to be added to make an Euler circuit in a graph with 6 vertices, where 4 vertices have degree 3 and 2 vertices have degree 2?
A: To create an Euler circuit, all vertices must have even degree.
We need to add 1 edge to each of the 4 vertices with degree 3.
Total edges to add: 4/2 = 2 edges
9. Use Ore’s theorem to determine if this graph has a Hamiltonian cycle:
A graph with 5 vertices where the degree sum of any two non-adjacent vertices is at least 5.
A: Ore’s theorem states that if the sum of degrees of any two non-adjacent vertices is ≥ n (where n is the number of vertices), then the graph has a Hamiltonian cycle.
Here, n = 5, and the condition is satisfied.
Therefore, this graph has a Hamiltonian cycle.
10. Apply Dirac’s theorem to determine if this graph has a Hamiltonian cycle:
A graph with 8 vertices, each having degree at least 4.
A: Dirac’s theorem states that if every vertex in a graph with n vertices (n ≥ 3) has degree ≥ n/2, then the graph has a Hamiltonian cycle.
Here, n = 8, and n/2 = 4.
Since each vertex has degree at least 4, Dirac’s theorem applies.
Therefore, this graph has a Hamiltonian cycle.
Practice Questions – Euler and Hamiltonian Paths
1. Determine if the following graph has an Euler circuit:
A graph with vertices {A, B, C, D, E} and edges {AB, BC, CD, DE, EA, AC, BD}
2. Does the complete graph K6 have a Hamiltonian cycle? If so, how many distinct Hamiltonian cycles does it have?
3. For a graph G with 7 vertices, each of degree 4, determine if it has:
a) An Euler path
b) A Hamiltonian path
4. Consider the Petersen graph. How many edges need to be added to create an Euler circuit?
5. Apply Ore’s theorem to determine if this graph has a Hamiltonian cycle:
A graph with 6 vertices where the degree sum of any two non-adjacent vertices is at least 6.
6. Does the complete bipartite graph K4,3 have:
a) An Euler path
b) A Hamiltonian cycle
7. In a graph with 8 vertices, what’s the minimum number of edges required to guarantee the existence of a Hamiltonian cycle according to Dirac’s theorem?
8. A graph G has 10 vertices. Five vertices have degree 4, three vertices have degree 3, and two vertices have degree 5. Does G have an Euler circuit? If not, can it have an Euler path?
9. Prove or disprove: If a graph has a Hamiltonian cycle, it must also have an Euler circuit.
10. Consider a graph G with 5 vertices and 7 edges. Is it possible for G to have both an Euler circuit and a Hamiltonian cycle? Justify your answer.
Applications in Engineering
1. Network Design
Hamiltonian paths and cycles are used in network design to ensure efficient routing and minimize the cost of network construction.
Example: Designing a fiber optic network that connects multiple cities with minimal cable length can be modeled as a Hamiltonian cycle problem.
2. Circuit Design
In electronic circuit design, Euler paths are used to design circuits that minimize the number of traces needed on a circuit board.
Example: Creating a circuit layout where each wire trace is used exactly once can be solved using an Euler path algorithm.
3. DNA Sequencing
Hamiltonian paths are used in bioinformatics for DNA sequencing, where the goal is to reconstruct the original sequence from overlapping fragments.
Example: Reconstructing a DNA sequence from short reads involves finding a Hamiltonian path through the overlap graph of the reads.
4. Robotics
Euler paths are used in robotics for route planning and covering every area of a space without retracing steps.
Example: Programming a robot vacuum to cover every part of a floor exactly once uses an Euler path algorithm.
5. Logistics and Routing
Hamiltonian paths and cycles are used in logistics to optimize delivery routes and minimize travel costs.
Example: Determining the most efficient route for a delivery truck to visit each customer exactly once and return to the depot can be solved using Hamiltonian cycle algorithms.
Conclusion – Euler and Hamiltonian Paths
Euler and Hamiltonian paths are essential concepts in graph theory with wide-ranging applications in network design, circuit design, DNA sequencing, robotics, and logistics. Understanding the conditions for the existence of these paths and cycles and applying appropriate algorithms can solve complex problems involving discrete structures and optimization.
FAQs on Euler and Hamiltonian Paths
What is the difference between an Euler path and a Hamiltonian path?
An Euler path visits every edge of a graph exactly once, while a Hamiltonian path visits every vertex of a graph exactly once.
What are the conditions for a graph to have an Euler circuit?
A graph has an Euler circuit if and only if it is connected and every vertex has an even degree.
Is there a simple condition for the existence of Hamiltonian cycles?
There is no simple necessary and sufficient condition for Hamiltonian cycles, but theorems like Dirac’s and Ore’s provide useful criteria.
How are Hamiltonian paths used in DNA sequencing?
Hamiltonian paths are used to reconstruct the original DNA sequence from overlapping fragments by finding a path through the overlap graph of the reads.
Can Euler paths be used in robotics?
Yes, Euler paths are used in robotics for route planning to cover every area of a space without retracing steps.
GATE CS Corner Questions
Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests. It is highly recommended that you practice them.
1. GATE CS 2007, Question 23
2. GATE CS 2005, Question 84
3. GATE CS 2008, Question 26
Please Login to comment...