C2 Pspice Experiment

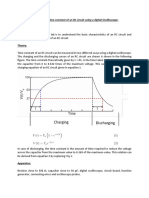
EXPERIMENT C2: PSPICE SIMULATION: STEP RESPONSE OF RC AND RLC CIRCUITS Associated course: KEEE1113 (Circuit Analysis 1) OBJECTIVES:
To analyse RC and RLC circuits EQUIPMENT: PC with PSpice software PRECAUTIONS: Follow the demonstrator instructions throughout the experiment REFERENCE(S): Refer to the main references of KEEE1113 (Circuit Analysis 1) TESTS: TEST 1: Pre-lab test TEST 2: RC circuit TEST 3: RLC circuit INTRODUCTION: The complete response of RC and RLC circuits to step inputs involves determination of the transient and steady state solutions of the circuit. Since the energy storage elements such as inductor and capacitor do not permit instantaneous change in energy, the transient part of the solution makes a smooth transition from one energy level to another. Thus a gradual change takes place from some initial level till the new steady state level is reached. Sudden loading of generator or a beam in a structure, sudden change in the setting of a value or failure of a hydraulic pump involves response due to step input. Step function apart from being mathematically simple to analyze, represents a rather severe type of disturbance appearing in the system. Moreover, an arbitrary function can be approximated in the form of a series of step input facilitates the finding of the response to any arbitrary input. The dynamic characteristics of a simple systems can be described by the first order(RC circuit) or second order(RLC circuit) differential equations. The complete response is then identified in two parts-complementary function(transient solution) and a particular integral(steady-state solution). It is always possible to obtain the complete response of complicated systems such as linear combination of first and second order systems. Although attention here is confined to electrical circuits, the same basic model can be used to represent a wide range of mechanical and, pneumatic or chemical systems. TEST 1: PRE-LAB 1. Series RC Circuit. For the circuit shown in Figure 1(R=470 , C=0.22uF), calculate the time constant(=RC). For R=220, recalculate the time constant. 2. Series RLC Circuit: For the circuit shown in Figure 2(L=10mH and C=1uF), the transfer function is given by
vc 1 /( LC ) = 2 VS s + ( R / L ) s + 1 /( LC )
Last updated on 9th July 2013
And, the two roots of the characteristic equation is

R 1 R = 2L LC 2L
2
2
s1, 2
a) b)
R 1 For critically damped response, is equal to be zero. Calculate R. LC 2L R 1 is less than zero. What is the range of For underdamped response, LC 2L suitable value for R? R 1 For overdamped response, is greater than zero. What is the range LC 2L of suitable value for R?
2 2
c)
TEST 2: RC CIRCUIT Objectives: 1. To observe and trace the complete response to step input 2. To determine the time constant and check with the theoretically calculated value
+ -
Figure 1. RC circuit 1. Construct the circuit as shown in Figure 1 using PSPICE ORCAD Capture Student. Set R=470 and C=0.22uF. For the voltage source, choose VPULSE from the SOURCE library. The parameters for the VPULSE are as follows: a) Low voltage, V1 = 0V e) Fall time, TF = 1ns b) High voltage, V2 = 5V f) Pulse width, PW = 1ms c) Time delay, TD = 0s g) Period, PER = 2ms d) Rise time, TR = 1ns 2. Go to PSPICE> Markers > Voltage Level. Place voltage level probes at the positive terminal of the VPULSE and capacitor. 3. Again, go to PSPICE > New Simulation Profile. On the New Simulation window, type Transient Analysis as the Name and none for the Inherit From. On the Simulation Settings window, choose Time Domain(Transient) as the Analysis Type. Set the Run Time to 2m seconds, Starting saving data after to 0 seconds and Maximum step size to 1u seconds. 4. Run the simulation. Sketch the input and output voltages as given by the simulation. Determine the rise time(10%-90%) and the time constant, from the output signal(i.e
capacitor). Compare the time constant to the theoretically calculated value (Hint: Use Cursor). 5. Change the resistor value to 220. Repeat step (4). Comment on the changes to rise time and time constant. TEST 3: RLC circuit Objectives: 1. (a) To adjust the parameter so that a critical response of the series RLC circuit is obtained. (b) To compare the critical resistance to the theoretical value. (c) To trace the response characteristics. 2. (a) To adjust the parameters so that an under damped response of the series RLC circuit is obtained and to observe and trace the response. (b) From the trace response, to obtain the period of oscillation, time constant and peak overshoot and compare these values to the theoretically calculated values. 3. (a) To adjust the parameter values so that an over damped response of the series RLC circuit is obtained. (b) To calculate the value of the damping coefficient and to check over damping character of the circuit. (c) To trace the response characteristics.
Figure 2. RLC circuit 1. Construct the circuit as shown in Figure 2 using PSPICE ORCAD Capture Student. Set L=10mH and C=1uF. For the voltage source, choose VPULSE from the SOURCE library. The parameters for the VPULSE are as follows: a) Low voltage, V1 = 0V e) Fall time, TF = 1ns b) High voltage, V2 = 5V f) Pulse width, PW = 50ms c) Time delay, TD = 0s g) Period, PER = 100ms d) Rise time, TR = 1ns 2. Goto PSPICE> Markers > Voltage Level. Place voltage level probes at the positive terminal of the VPULSE and capacitor. 3. Again, goto PSPICE > New Simulation Profile. On the New Simulation window, type Transient Analysis as the Name and none for the Inherit From. On the Simulation Settings window, choose Time Domain(Transient) as the Analysis Type. Set the Run Time to 5m seconds, Starting saving data after to 0 seconds and Maximum step size to 1u seconds. 4. Set the resistor value, Rc for a critically damped response as calculated in the prelab. Run the simulation and sketch the result. Determine the time constant and rise time (10%-90%).
5. For underdamped response, set the resistor value, Ru to Rc/5. Run the simulation and sketch the result. From the result, determine the following: a) Period of oscillation(compare to the theoretically calculated values) b) Time constant and Rise time (10%-90%) c) Peak overshoot 6. For overdamped response, set the resistor value Ro, to 3*Rc. Run the simulation and sketch the result. From the result, determine the time constant and rise time(10%90%). APPENDIX Step Response to RLC Circuit
Rise Time/Time Constant
Peak Overshoot/ Period of Oscillation
END OF EXPERIMENT

C2 Pspice Experiment

Uploaded by

Copyright:

Available Formats

C2 Pspice Experiment

Uploaded by

Document Information

Original Description:

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

C2 Pspice Experiment

Uploaded by

Copyright:

Available Formats

EXPERIMENT C2: PSPICE SIMULATION: STEP RESPONSE OF RC AND RLC CIRCUITS Associated course: KEEE1113 (Circuit Analysis 1) OBJECTIVES:

Last updated on 9th July 2013

And, the two roots of the characteristic equation is

Last updated on 9th July 2013

Last updated on 9th July 2013

Rise Time/Time Constant

Last updated on 9th July 2013

Peak Overshoot/ Period of Oscillation

Last updated on 9th July 2013

You might also like