Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
236 views

Functions Practice Problems

This document provides 11 practice problems for students covering functions and operations on functions for an IB Mathematics SL chapter 2 exam. It instructs students to show their work, check their answers, and do the problems on separate paper. The 11 problems cover topics like composing functions, finding inverse functions, evaluating functions, and solving quadratic equations using different methods. It concludes by asking students to reflect on their strengths and weaknesses with the chapter material and their plan to prepare for upcoming assessments.

Uploaded by

taengoo
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
236 views

Functions Practice Problems

This document provides 11 practice problems for students covering functions and operations on functions for an IB Mathematics SL chapter 2 exam. It instructs students to show their work, check their answers, and do the problems on separate paper. The 11 problems cover topics like composing functions, finding inverse functions, evaluating functions, and solving quadratic equations using different methods. It concludes by asking students to reflect on their strengths and weaknesses with the chapter material and their plan to prepare for upcoming assessments.

Uploaded by

taengoo
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 4

IB Mathematics SL

Chapter 2 Practice Problems Functions

Name___________________

Mr. Wagner is again trying to cut down on paper usage, so youll probably want to do these problems on
a separate sheet of paper and put your notebooks to work. On a real exam, as youve seen, youll have
much more room to work with!
Get in the habit of (a) showing all necessary reasoning (2) making your answers obvious and (3) checking
your work and answers against the markscheme. Are you always checking your answers in general?
Remember that solutions to every problem you have as review, including book work, are provided.
1.

Consider f(x) =
(a)

x5 .

Find
(i)

f(11);

(ii)

f(86);

(iii)

f(5).
(3)

(b)

Find the values of x for which f is undefined.


(2)

(c)

Let g(x) = x2. Find (g f)(x).


(2)
(Total 7 marks)

2.

Let f (x) =

x + 4 , x 4 and g (x) = x2, x

(a)

Find (g f ) (3).

(b)

Find f 1(x).

(c)

Write down the domain of f 1.

(Total 6 marks)

3.

Let f(x) = 7 2x and g(x) = x + 3.


(a)

Find (g f)(x).
(2)

(b)

Write down g1(x).


(1)

(c)

Find (f g1)(5).
(2)
(Total 5 marks)

IB Questionbank Maths SL 1 and Ian Wagner

4.

Let f(x) = 3x, g(x) = 2x 5 and h(x) = (f g)(x).


(a)

Find h(x).
(2)

(b)

Find h1(x).
(3)
(Total 5 marks)

5.

Let f(x) = x2 + 4 and g(x) = x 1.


(a)

Find (f g)(x).
(2)

(The remainder of this problem would be considered an extension or challenge. However, given that the
equation of h is given in (c), see if you can answer (d)!)
3
The vector translates the graph of (f g) to the graph of h.
1

(b)

Find the coordinates of the vertex of the graph of h.


(3)

(c)

Show that h(x) = x2 8x + 19.


(2)

(d)

The line y = 2x 6 is a tangent to the graph of h at the point P. Find the x-coordinate of P.
(5)
(Total 12 marks)

6.

Let f(x) = x2 and g(x) = 2x 3.


(a)

Find g1(x).
(2)

(b)

Find (f g)(4).
(3)
(Total 5 marks)

7.

The functions f and g are defined by f : x 3x, g : x x + 2.


(a)

Find an expression for (f g)(x).


(2)

(b)

Find f1(18) + g1(18).


(4)
(Total 6 marks)

IB Questionbank Maths SL 2 and Ian Wagner

8.

Let f (x) = x3 4 and g (x) = 2x.


(a)

Find (g f ) (2).

(b)

Find f 1 (x).
(Total 6 marks)

9.

Let g (x) = 3x 2, h (x) =

5x
, x 4.
x4

(a)

Find an expression for (h g) (x). Simplify your answer.

(b)

Solve the equation (h g) (x) = 0.


(Total 6 marks)

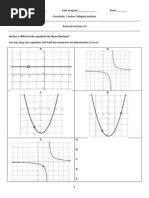
10.

Let f (x) = p

3x
, where p, q
x q2
2

Part of the graph of f, including the asymptotes, is shown below.

(a)

The equations of the asymptotes are x =1, x = 1, y = 2. Write down the value of
(i)

p;

(ii)

q.
(2 marks)

IB Questionbank Maths SL 3 and Ian Wagner

(b)

Find all intercepts of the function (x-intercepts and y-intercepts) algebraically

(4 marks)

11. You will also need to be prepared to solve a quadratic by these three means: Factoring, completing
the square and the quadratic formula. Use all three of these methods to solve: 4 x 2 20 x 56 =
0

Personal Reflection
Please do on separate paper and submit to Mr. W. USE COMPLETE SENTENCES
and be THOUGHTFUL.
At this point, youve worked a lot of book and practice problems, and have had the chance to
assess your own learning.
What are your strengths in Chapter 2?
Where are your weaknesses?
What is your plan to prepare for the unit quiz and unit assessments?

IB Questionbank Maths SL 4 and Ian Wagner

You might also like