Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd Logo
Upload

Welcome to Scribd!

  • 2K views

    Gaussian Integers: (30 Marks) Gaussian Integer Is A Complex Number

    Uploaded by

    Edasu Güvenç
    (1) The document discusses Gaussian integers, which are complex numbers of the form a + bi where a and b are integers. (2) It asks several questions about divisibility properties and primality of Gaussian integers. (3) Key concepts covered include the norm of a Gaussian integer, Gaussian primes, and using norms to determine whether one Gaussian integer divides another.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd

    Gaussian Integers: (30 Marks) Gaussian Integer Is A Complex Number

    Uploaded by

    Edasu Güvenç
    2K views1 page
    (1) The document discusses Gaussian integers, which are complex numbers of the form a + bi where a and b are integers. (2) It asks several questions about divisibility properties and primality of Gaussian integers. (3) Key concepts covered include the norm of a Gaussian integer, Gaussian primes, and using norms to determine whether one Gaussian integer divides another.

    Original Title

    analysis_practice_paper_3_en-7

    Copyright

    © © All Rights Reserved

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    (1) The document discusses Gaussian integers, which are complex numbers of the form a + bi where a and b are integers. (2) It asks several questions about divisibility properties and primality of Gaussian integers. (3) Key concepts covered include the norm of a Gaussian integer, Gaussian primes, and using norms to determine whether one Gaussian integer divides another.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    2K views1 page

    Gaussian Integers: (30 Marks) Gaussian Integer Is A Complex Number

    Uploaded by

    Edasu Güvenç
    (1) The document discusses Gaussian integers, which are complex numbers of the form a + bi where a and b are integers. (2) It asks several questions about divisibility properties and primality of Gaussian integers. (3) Key concepts covered include the norm of a Gaussian integer, Gaussian primes, and using norms to determine whether one Gaussian integer divides another.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    of 1

    Gaussian integers

    [30 marks]

    A Gaussian integer is a complex number, z , such that z= a + bi where a, b ∈  . In this question, you are
    asked to investigate certain divisibility properties of Gaussian integers.

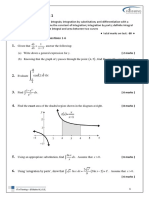
    Consider two Gaussian integers, α = 3 + 4i and β = 1 − 2i , such that γ = αβ for some Gaussian integer γ .

    (a) Find γ. [2]

    Now consider two Gaussian integers, α = 3 + 4i and γ= 11 + 2i .

    γ
    (b) Determine whether is a Gaussian integer. [3]
    α

    The norm of a complex number z , denoted by N ( z ) , is defined by N ( z ) = z 2 . For example, if z= 2 + 3i


    then N ( 2 + 3i ) = 22 + 32 = 13 .

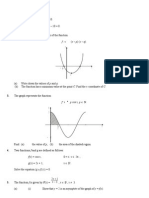
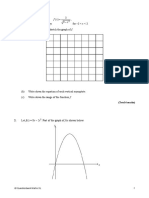
    (c) On an Argand diagram, plot and label all Gaussian integers that have a norm less than 3.
    [2]

    (d) Given that α= a + bi where a, b ∈  , show that N (α=


    ) a 2 + b2 .
    [1]

    A Gaussian prime is a Gaussian integer, z , that cannot be expressed in the form z = αβ where α , β are
    Gaussian integers with N (α ) , N ( β ) > 1 .

    (e) = c 2 + d 2 as a product of two Gaussian integers each of norm


    By expressing the positive integer n
    2 2
    n
    c + d , show that is not a Gaussian prime. [3]

    The positive integer 2 is a prime number, however it is not a Gaussian prime.

    (f) Verify that 2 is not a Gaussian prime. [2]

    (g) Write down another prime number of the form c 2 + d 2 that is not a Gaussian prime and express it as a
    product of two Gaussian integers. [2]

    Let α , β be Gaussian integers.

    (h) Show that N (αβ ) = N (α ) N ( β ) . [6]

    The result from part (h) provides a way of determining whether a Gaussian integer is a Gaussian prime.

    (i) Hence show that 1 + 4i is a Gaussian prime. [3]

    (j) Use proof by contradiction to prove that a prime number, p , that is not of the form a 2 + b 2 is a
    Gaussian prime. [6]

    You might also like