Correlation
Correlation
Uploaded by
iconhiq.editsCopyright:
Available Formats
Correlation
Correlation
Uploaded by
iconhiq.editsCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Copyright:
Available Formats
Correlation
Correlation
Uploaded by
iconhiq.editsCopyright:
Available Formats
CORRELATION
Correlation analysis studies the relation between two variables. Correlation studies and
measures the direction and intensity of relationship among variables. Correlation measures
covariation and not causation.
Univariate distributions are those where observations are given on a single variable. We
obtained a measure of central tendency and a measure of dispersion of the set of values of the
variable.
Suppose we have observations on two variables, X and Y for several individuals. This is a
bivariate distribution. We can calculate the central value and dispersion of each variable
separately. However to know the association between the two variables we study the
correlation between the two.
Correlation between two variables X and Y mean that when the value of one variable is found
to change in one direction the value of the other variable is found to change either in the same
direction or in the opposite direction but in a definite way.
In the words of Croxton and Cowden ‘ when the relationship is of a quantitative nature, the
appropriate statistical tool for discovering and measuring the relationship and expressing it in
a brief formula is known as correlation.
IMPORTANCE OF CORRELATION
1. Measurement of relationship- the coefficient of correlation facilitates measurement of
extent of relationship between two variables. Eg bivariate distributions can be studied
2. Facilitates regression- when there is correlation between two variables the value of
one variable can be estimated given the value of another variable. Regression
equations can be used to find such values.
3. Facilitates decision making- decision making becomes feasible because the trend of
change in one variable resulting in change in the other variable can be studied and
important decisions can be made.
4. Formulation of policies- correlation analysis facilitates understanding of economic
behaviour because of existence of relationship between two or more variables and
helps in formulating and implementing certain policies.
TYPES OF CORRELATION
1. On the basis of direction of change
a) Negative correlation
b) Positive correlation
2. On the basis of degree of change
a) Linear correlation
b) Non linear correlation
3. On the basis of number of variables
a) Simple correlation
b) Partial correlation
c) Multiple correlation
1. On the basis of direction of change correlation can be classified as positive
or negative. Positive correlation is when both the variables move in the
same direction. ie; both of them increases or decreases. On the other hand,
negative correlation is when both the variables move in opposite
directions. ie; when one decreases the other increases and vice versa.
2. The correlation is said to be linear if the ratio of change between two
variables is constant or fixed. In other words there is proportionate change
in the values of the two variables. If two sets of data are plotted on a graph
paper the relationship will be indicated by a straight line. It is also known
as perfect correlation. Linear or perfect correlation maybe positive or
negative.
Non linear correlation or curvilinear correlation is said to be non linear if
the ratio of change between the two variables is not constant. There is no
proportionate change in the values of the two variables and when plotted
on a grave paper the relationship will not make a straight line on the graph
paper. It may be positive or negative.
3. In simple correlation we study the relationship between two variables
involved in a statistical study. In a partial correlation more than two
variables are involved in the statistical study and out of these variables we
study the relationship between only two variables and all other factors are
assumed to remain constant. In a multiple correlation more than two
variables are involved in statistical study and the relationship between
them are studied simultaneously and none of them are assumed to be
constant.
DEGREE OF CORRELATION
1. Perfect correlation
2. Absence of correlation
3. Limited degree of correlation
1. Perfect correlation is that where changes in two related variables are exactly
proportional. If equal proportion changes occur in the same direction then the
value is described as +1. If equal proportionate changes occur in the reverse
direction then the value is described as -1.
2. Absence of correlation or zero correlation does not imply the absence of
relationship between the two variables, it implies that the values are uncorrelated.
3. Limited degree of correlation refers to a situation when a change in one variable
need not be exactly accompanied by a corresponding change in the other variable.
It is a situation between 0 and (+/- )1. This can be further classified as
a. High degree of correlation- if the coefficient of correlation lies between + and
– 0.75 to 1
b. Moderate degree of correlation- if coefficient of correlation lies between
(+/-)0.25 to (+/-) 0.75 it is known as moderate degree of positive/negative
correlation respectively
c. Low degree of Correlation – if the coefficient of correlation lies between
(+and –) 0 and 0.25
METHODS OF ESTIMATING CORRELATION
1. Scatter Diagram
2. Karl Pearson’s coefficient of correlation method
3. Spearman’s rank correlation coefficient method
1. Scatter diagram is a simple method of measuring correlation. It is
a graphic presentation of relation between two variables. It offers
direction and degree of change between two variables graphically
The X variable is taken on the horizontal axis and the Y variable is
plotted on the vertical axis and a point is plotted for each variable.
After the entire data is plotted a cluster of points is obtained on the
graph paper. The trend between the plotted points is observed and the
direction and degree of relationship between the X and the Y variables
is studied.
The following diagrams give us the relationship between the two
variables and help us to study the trend.
1. Perfect Positive Correlation
2. Perfect Negative Correlation
3. Limited Degree of Correlation
a. High Degree of positive correlation
b. Low degree of positive correlation
c. High degree of negative correlation
d. Low degree of negative correlation
4. Absence of correlation or no correlation
Merits of scatter diagram
1. Easy to draw
2. Helps to determine whether the relationship between X and Y
is Linear or Non Linear
3. In case of a linear relationship gives a clear visual picture
Demerits of scatter diagram
1. The degree of association between two variables cannot be
determined in numerical terms from a scatter diagram
2. It is not possible to draw a scatter diagram on graph paper if
there are more than two variables
Karl Pearson’s Coefficient of Correlation
This method overcomes the limitation of scatter diagram of not indicating precise magnitude
of correlation.
Calculating with Actual mean method
Calculating with direct method
1. We calculate the sum of values of series X and get summation of X
2. We calculate the sum of values of series Y and get summation of Y
3. We find squares of values of series X and get summation X square
4. We find the squares of values of series Y and get summation Y square
5. We find the product of the values of series X and Series y and get summation XY
Merits of Karl Pearson’s Coefficient of Correlation
1. It gives exact measurement of the correlation between the variables
2. Expresses the direction and degree of change in the two variables
3. Interpretation of results become easy as this method gives us precise magnitude of
the correlation.
Demerits of Karl Pearson’s Coefficient of Correlation
1. The method cannot be used to quantify qualities
2. Since the method is based on arithmetic mean the values of correlation is
largely affected by the values of extreme items.
Spearman’s Rank Correlation
This method is used when the variables cannot be measured in quantitative
terms. This method provides a measure of linear association between ranks
assigned to individuals according to the quality of their attributes.
There are three types of sums that we need to cover here
1. When ranks are given
2. When ranks are not given
3. When ranks are repeated
Merits
1. It is a simple and easy method to calculate coefficient of correlation
2. Suitable in case of qualitative distribution such as honesty, intelligence
3. Sometimes the correlation coefficient between two variables with
extreme values may be quite different from the coefficient without the
extreme values (simple correlation which is based on arithmetic mean
and standard deviation). Here the rank correlation provides a better
alternative to simple correlation.
Demerits
1. If there is a large number of observations the method is not suitable
2. This method has limited use when group frequency is given
3. This method ignores the actual magnitude of data and the results
are not exact because the effect of the actual values are not studied.
Line of best fit is the one that passes through the scattered points such that it represents most
of these points. Roughly half of the scattered points should be on either side of the line.
----------------------------------------------------------------------------------------------------------------
You might also like
- Methods Matter PDFDocument414 pagesMethods Matter PDFestgutiep100% (1)
- Assignment#2 RT WQ2021Document2 pagesAssignment#2 RT WQ2021Manoj VemuriNo ratings yet
- Assignment On CorrelationDocument7 pagesAssignment On CorrelationLucky Sharma100% (1)
- Rdy Ccss Math Gr7 Ratios Involving Complex Fractions 19498Document50 pagesRdy Ccss Math Gr7 Ratios Involving Complex Fractions 19498JenonymouslyNo ratings yet
- Correlation and Regression AnalysisDocument100 pagesCorrelation and Regression Analysishimanshu.goelNo ratings yet
- Summarize The Methods of Studying Correlation.: Module - 3Document17 pagesSummarize The Methods of Studying Correlation.: Module - 3aditya devaNo ratings yet
- ECAP790 U06L01 CorrelationDocument37 pagesECAP790 U06L01 CorrelationPrince GuptaNo ratings yet
- CorrelationDocument13 pagesCorrelationMayankNo ratings yet
- Correlation and RegressionDocument64 pagesCorrelation and RegressionDilshajNo ratings yet
- Correlation and RegressionDocument17 pagesCorrelation and Regressionsujnahere7435100% (1)
- Unit 2 - (A) Correlation & RegressionDocument15 pagesUnit 2 - (A) Correlation & RegressionsaumyaNo ratings yet
- Unit 3Document24 pagesUnit 3swetamakka1026No ratings yet
- PeterDocument48 pagesPeterPeter LoboNo ratings yet
- Correlation 180511133644Document12 pagesCorrelation 180511133644Simmi KhuranaNo ratings yet
- Correlation 180511133644Document12 pagesCorrelation 180511133644Simmi KhuranaNo ratings yet
- Online Class Etiquettes and Precautions For The StudentsDocument49 pagesOnline Class Etiquettes and Precautions For The StudentsProtikNo ratings yet
- Correlation and Types of Correlation 29Document14 pagesCorrelation and Types of Correlation 29AKSHAY SANTHOSH SANTHOSH SACHARIASNo ratings yet
- Correlation: (For M.B.A. I Semester)Document46 pagesCorrelation: (For M.B.A. I Semester)Arun Mishra100% (2)
- Types of CorrelationDocument3 pagesTypes of CorrelationRenee San Gabriel ReyesNo ratings yet
- Session 3 SummaryDocument42 pagesSession 3 SummaryJuank Z BkNo ratings yet
- Correlation SBCDocument4 pagesCorrelation SBCpd0290001No ratings yet
- Makaku PDFDocument3 pagesMakaku PDFcacied1No ratings yet
- CorrelationDocument17 pagesCorrelationSara GomezNo ratings yet
- Correlation Coefficient in Medical ResearchDocument6 pagesCorrelation Coefficient in Medical ResearchMyanmar LearnersNo ratings yet
- Stat-CORRELATION & REGRESSION ANALYSISDocument79 pagesStat-CORRELATION & REGRESSION ANALYSISAkshitha KulalNo ratings yet
- Correlation and Simple Linear Regression Analyses: ObjectivesDocument6 pagesCorrelation and Simple Linear Regression Analyses: ObjectivesMarianne Christie RagayNo ratings yet
- Initially Developed by Sir Francis Galton (1888) and Karl Pearson (1896)Document10 pagesInitially Developed by Sir Francis Galton (1888) and Karl Pearson (1896)Nirav PatelNo ratings yet
- CorrelationDocument27 pagesCorrelationAniket ChauhanNo ratings yet
- CorrelationDocument8 pagesCorrelationPooja vidhyasagarNo ratings yet
- Correlation: Self Instructional Study Material Programme: M.A. Development StudiesDocument21 pagesCorrelation: Self Instructional Study Material Programme: M.A. Development StudiesSaima JanNo ratings yet
- Correlation Analysis Notes-2Document5 pagesCorrelation Analysis Notes-2Kotresh KpNo ratings yet
- Correlational Research EssayDocument6 pagesCorrelational Research EssayfadhilNo ratings yet
- Correlation Analysis: Concept and Importance of CorrelationDocument8 pagesCorrelation Analysis: Concept and Importance of CorrelationGanesh BabuNo ratings yet
- Statistic Notes For Third Year B.Com.Document3 pagesStatistic Notes For Third Year B.Com.Vicky GadhiaNo ratings yet
- Correlation in SPSSDocument2 pagesCorrelation in SPSSRyenFoongChanYen100% (1)
- Correlation RegressionDocument5 pagesCorrelation RegressionAbrar AhmadNo ratings yet
- Stat - 7 Correlation and Regression AnalysisDocument9 pagesStat - 7 Correlation and Regression AnalysisRAISHANo ratings yet
- STATISTICS DocumentaryDocument18 pagesSTATISTICS Documentarykeerthikabalasubramanian7No ratings yet
- Regression Analysis: Definition: The Regression Analysis Is A Statistical Tool Used To Determine The Probable ChangeDocument12 pagesRegression Analysis: Definition: The Regression Analysis Is A Statistical Tool Used To Determine The Probable ChangeK Raghavendra Bhat100% (1)
- Etha Seminar Report-Submitted On 20.12.2021Document12 pagesEtha Seminar Report-Submitted On 20.12.2021AkxzNo ratings yet
- Research in Daily Life 2Document11 pagesResearch in Daily Life 2ameracasanNo ratings yet
- Africa Beza College: Chapter 2: Correlation Theory Pre-Test QuestionsDocument11 pagesAfrica Beza College: Chapter 2: Correlation Theory Pre-Test QuestionsAmanuel GenetNo ratings yet
- Types of Correlation and Their Specific ApplicationsDocument25 pagesTypes of Correlation and Their Specific ApplicationsRajesh KannaNo ratings yet
- UNIT-3 Correlation Is A Bivariate Analysis That Measures The Strength of AssociationDocument4 pagesUNIT-3 Correlation Is A Bivariate Analysis That Measures The Strength of AssociationHARSH ASWANINo ratings yet
- Correlation Coefficient's AssignmentDocument7 pagesCorrelation Coefficient's AssignmentIsrahana Shahril100% (1)
- Machine Learning NotesDocument23 pagesMachine Learning NotesMuthukumar V P CS&CANo ratings yet
- Hsslive-Xii-Statistics-1. Correlation Analysis-EnglishDocument6 pagesHsslive-Xii-Statistics-1. Correlation Analysis-EnglishpravgonemadNo ratings yet
- Module 7 Data Management Regression and CorrelationDocument11 pagesModule 7 Data Management Regression and CorrelationAlex YapNo ratings yet
- Report Statistical Technique in Decision Making (GROUP BPT) - Correlation & Linear Regression123Document20 pagesReport Statistical Technique in Decision Making (GROUP BPT) - Correlation & Linear Regression123AlieffiacNo ratings yet
- Using Statistical Techniq Ues in Analyzing DataDocument40 pagesUsing Statistical Techniq Ues in Analyzing Datadanielyn aradillos100% (1)
- Quantitative Technique Unit 2Document9 pagesQuantitative Technique Unit 2Aditya GuptaNo ratings yet
- Assignment On Correlation Analysis Name: Md. Arafat RahmanDocument6 pagesAssignment On Correlation Analysis Name: Md. Arafat RahmanArafat RahmanNo ratings yet
- Correlation: HapterDocument16 pagesCorrelation: HapterRiaNo ratings yet
- STAT Week7Document59 pagesSTAT Week7crespyadrian2006No ratings yet
- Module 7 CorrelationDocument24 pagesModule 7 CorrelationLavanya ShettyNo ratings yet
- Correlational Analysis - Statistics - Alok - KumarDocument42 pagesCorrelational Analysis - Statistics - Alok - KumarNana Kow Bentum AIDOONo ratings yet
- 2020 CorrelationDocument5 pages2020 CorrelationOcyub Avlas OdnamraNo ratings yet
- Class 11 Statistics Best Notes For English Medium Chapter-6 CorrelationDocument14 pagesClass 11 Statistics Best Notes For English Medium Chapter-6 CorrelationAasimNo ratings yet
- Correlation Analysis-Students NotesMAR 2023Document24 pagesCorrelation Analysis-Students NotesMAR 2023halilmohamed830No ratings yet
- Correlation Coefficient: Group 5: - Willy - Intan Dani SitumorangDocument13 pagesCorrelation Coefficient: Group 5: - Willy - Intan Dani SitumorangIntan SitumorangNo ratings yet
- Direct Linear Transformation: Practical Applications and Techniques in Computer VisionFrom EverandDirect Linear Transformation: Practical Applications and Techniques in Computer VisionNo ratings yet
- Freeman Et Al 2007 Sense of BelongingDocument19 pagesFreeman Et Al 2007 Sense of BelongingperryNo ratings yet
- Exploratory Data AnalysisDocument3 pagesExploratory Data Analysispontas97No ratings yet
- Experiments in Ceramic Technology The Effects of Various Tempering Materials On Impact and Thermal Shock Resistamce Bronitsky 1986Document14 pagesExperiments in Ceramic Technology The Effects of Various Tempering Materials On Impact and Thermal Shock Resistamce Bronitsky 1986Rigel AldebaránNo ratings yet
- Nursing Research Chapter 1Document56 pagesNursing Research Chapter 1Jwllyn CCNo ratings yet
- Journal An Empirical Study On The Effectiveness of Work-Life Balance in Banking IndustryDocument3 pagesJournal An Empirical Study On The Effectiveness of Work-Life Balance in Banking IndustryAmirrul IdhamNo ratings yet
- Amazon Inventory Reconciliation Using AI: ST ND RDDocument6 pagesAmazon Inventory Reconciliation Using AI: ST ND RDsumangal chhaudaNo ratings yet
- Blood Parasites of House Finches (Carpodacus Mexican Us) From Georgia and New York - 2008Document6 pagesBlood Parasites of House Finches (Carpodacus Mexican Us) From Georgia and New York - 2008EsTeban PeñaNo ratings yet
- Rancangan NestedDocument23 pagesRancangan NestedsidajatengNo ratings yet
- This Question Paper Contains 02 PagesDocument2 pagesThis Question Paper Contains 02 PagesMaster ChiefNo ratings yet
- 2012 - Dawson - Dichotomizing Continuous Variables in Statistical Analysis - A Practice To AvoidDocument2 pages2012 - Dawson - Dichotomizing Continuous Variables in Statistical Analysis - A Practice To AvoidAbdul HadiNo ratings yet
- 2.0 Chapt 1-3Document34 pages2.0 Chapt 1-3Rhea Angela CabristanteNo ratings yet
- Engineering Formula Sheet: StatisticsDocument1 pageEngineering Formula Sheet: Statisticskrishna_pipingNo ratings yet
- Core-EPS 203 Intro To Educational ResearchDocument235 pagesCore-EPS 203 Intro To Educational ResearchProsper Boateng-HodoNo ratings yet
- On Board Diagnosis For Three-Way Catalytic ConvertersDocument33 pagesOn Board Diagnosis For Three-Way Catalytic ConvertersMaher Al-busaidiNo ratings yet
- Cable Diagnosis Based On Defect Location and Characterization Through Partial Discharge MeasurementsDocument8 pagesCable Diagnosis Based On Defect Location and Characterization Through Partial Discharge Measurementsbmwr1100s_055542No ratings yet
- Difficulties of Grade 12 Abm Students Towards Fundamentals of Accountancy Business and ManagementDocument50 pagesDifficulties of Grade 12 Abm Students Towards Fundamentals of Accountancy Business and ManagementJanna GunioNo ratings yet
- Casio Scientific Calculator Fx-570msDocument26 pagesCasio Scientific Calculator Fx-570msaimarashidNo ratings yet
- Statistics and Optimization Techniques OCT 2022Document4 pagesStatistics and Optimization Techniques OCT 2022Dr Praveen KumarNo ratings yet
- Onobrakpeya, & Ugwuonah, 2023Document20 pagesOnobrakpeya, & Ugwuonah, 2023alaaelkholi99No ratings yet
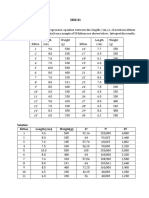
- Kitten Length (CM) Weight (G) : SolutionDocument4 pagesKitten Length (CM) Weight (G) : SolutionCyndi CascaroNo ratings yet
- Askep PeritonitisDocument6 pagesAskep PeritonitisLeni AnggrainiNo ratings yet
- Mod Project SRKDocument65 pagesMod Project SRKSrk Siva IyerNo ratings yet
- Stat263 PDFDocument540 pagesStat263 PDFYunuo HuangNo ratings yet
- Lab 03 - Duo-Trio, Triangle, Tetrad TestDocument10 pagesLab 03 - Duo-Trio, Triangle, Tetrad TestEdison SutionoNo ratings yet
- Math 7 - Curriculum Map - 2021-2022Document5 pagesMath 7 - Curriculum Map - 2021-2022Hassel Abayon0% (1)
- Total Qualty ManagementDocument82 pagesTotal Qualty Managementazdvvs100% (2)
- Social Media Overload: A Correlational Study Between Social Media Use (Facebook) and Social Behavior of The Senior High School Students of Dvoref-ShsDocument54 pagesSocial Media Overload: A Correlational Study Between Social Media Use (Facebook) and Social Behavior of The Senior High School Students of Dvoref-ShsCharles Pangue100% (1)