ダイナミック‐プログラミング【dynamic programming】
読み方:だいなみっくぷろぐらみんぐ
ディー‐ピー【DP】
動的計画
【英】:dynamic programming
概要
1957年, ベルマン (R.E. Bellman) によって提案された多変数最適化問題を解くための手法. 目的関数に再帰性(可分性)と単調性があり, 制約式が逐次的であるとき, 原問題をある部分問題群に埋め込んで, 各部分問題の最適値を定義し, 相隣る問題の最適値間の関係式(再帰式)を導く. これを逐次解いて, 最後に与問題の最適解を求める方法である. 解法の効率化のためには, 決定変数, 状態変数, 評価関数などの選択・設定に個々の創意工夫を要する.
詳説
多変数最適化問題の目的関数が再帰性(可分性)と単調性をもち, 制約条件に逐次性があるとき, 再帰式 を導いて, これを1変数ずつ解いて最後に与問題の最適解を求めようとする方法を, 動的計画(dynamic programming)と呼ぶ. 原理としては  最適性の原理 (principle of optimality),
最適性の原理 (principle of optimality),  不変埋没原理(principle of invariant imbedding),
不変埋没原理(principle of invariant imbedding),  因果律の原理(principle of causality), の三つに基づく[1]. 最適性の原理には
因果律の原理(principle of causality), の三つに基づく[1]. 最適性の原理には  オリジナル版,
オリジナル版,  シンプル版,
シンプル版,  "
" "版,
"版,  構造解析版,
構造解析版,  数学版, などがある[9]. 数学的にはマックスマックス定理 に遡ることができる[2][4]. 応用面では, 逐次決定過程 [3][6]の基本原理として用いられ, マルコフ決定過程の政策改良法, 最短経路問題のダイクストラ法, 巡回セールスマン問題など種々の最適化問題の解法としてアルゴリズムに組み込まれている.
数学版, などがある[9]. 数学的にはマックスマックス定理 に遡ることができる[2][4]. 応用面では, 逐次決定過程 [3][6]の基本原理として用いられ, マルコフ決定過程の政策改良法, 最短経路問題のダイクストラ法, 巡回セールスマン問題など種々の最適化問題の解法としてアルゴリズムに組み込まれている.


で定義する. 構成要素の1変数関数  がすべて単調な(狭義単調な)とき, 特に単調性(狭義単調性)をもつ再帰型関数という. 単調性をもつ再帰型関数
がすべて単調な(狭義単調な)とき, 特に単調性(狭義単調性)をもつ再帰型関数という. 単調性をもつ再帰型関数  を目的式と制約式にする主問題
を目的式と制約式にする主問題


に埋め込み, この最大値を  とする. このとき, 制約式の狭義単調性と両式の連続性を仮定すると, 再帰式
とする. このとき, 制約式の狭義単調性と両式の連続性を仮定すると, 再帰式
 |
 |
が成り立つ. ただし,  は
は  の逆関数. この再帰式を後向きに解いて, 最後に主問題の最大値
の逆関数. この再帰式を後向きに解いて, 最後に主問題の最大値  が得られる. これが動的計画法である. さらに, 主問題
が得られる. これが動的計画法である. さらに, 主問題  と逆問題
と逆問題

の解(最小値関数と最小点関数)の間には互いに逆関数の関係にある(逆定理 [5]). これは線形計画における双対定理に類似して, 動的計画の双対定理と考えられる[11].

で表わされる. これに対して反転関数(逐次パラメトリック逆関数)  を
を

で定義する. このとき, 目的式 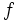 , 制約式
, 制約式  (ただし
(ただし  をもつ主問題の反転問題を
をもつ主問題の反転問題を

で考えると, 反転問題の最小値は主問題の終端値となる (反転定理 [7]).
さらに, 準線形化, 最大変換(共役変換)による双対理論を組み込んだ三面鏡理論 [8]が制御過程上で展開されている. 逆問題, 反転問題, 双対問題は基本的に動的計画法で解くことができるが, それぞれの問題の最適解は直接解くことなく, 対応する定理によって得られる[7].
再帰性, 単調性がない場合の最適化としては, 非可分性との関連で結合性などの下で事前条件付き決定過程, 事後条件付き決定過程[10]がファジィ動的計画, 非加法型再帰的効用関数の経済学などで研究されている. これらの問題はマルコフ政策のクラスで再帰式が導かれる.
[1] R. Bellman, Dynamic Programming, Princeton Univ. Press, 1957.
[2] G. H. Hardy, J. E. littlewood and G. Pólya, Inequalities, 2nd ed., Cambridge Univ. Press, 1952.
[3] 茨木俊秀,『組合せ最適化の理論』, 電子通信学会, 1979.
[4] 伊理正夫ほか, 座談会「最大問題最小問題をめぐって」,『数学セミナー』, 7月号 (1966), 40-48.
[5] S. Iwamoto, "Inverse Theorems in Dynamic Programming I, II, III," Journal of Mathematical Analysis and Applications, 58 (1977), 113-134, 249-279, 439-448.
[6] 岩本誠一,「逐次決定過程としての動的計画論I,II」,『オペレーションズ・リサーチ』, 22 (1977), 427-434, 496-501.
[7] 岩本誠一,『動的計画論』, 九州大学出版会(経済工学シリーズ), 1987.
[8] S. Iwamoto, "A three mirror problem on dynamic programming," in Proceedings of the Third Bellman Continuum Workshop, 363-382, 1989.
[9] 岩本誠一,「動的計画の最近の進歩」, 第2回RAMPシンポジウム論文集, 129-140, 1990.
[10] S. Iwamoto, "Conditional decision processes with recursive reward function,"Journal of Mathematical Analysis and Applications, 230 (1999), 193-210.
動的計画法
動的計画法(どうてきけいかくほう、英: Dynamic Programming, DP)は、計算機科学の分野において、アルゴリズムの分類の1つである。対象となる問題を複数の部分問題に分割し、部分問題の計算結果の記録を利用して全体の問題を解く手法を総称してこう呼ぶ。
定義
細かくアルゴリズムが定義されているわけではなく、下記2条件を満たすアルゴリズムの総称である。
- 帰納的な関係の利用:より小さな問題例の解や計算結果を帰納的な関係を利用してより大きな問題例を解くのに使用する。
- 計算結果の記録:小さな問題例、計算結果から記録し、同じ計算を何度も行うことを避ける。帰納的な関係での参照を効率よく行うために、計算結果は整数、文字やその組みなどを見出しにして管理される。
概要
「動的計画法(dynamic programming)」という言葉は1940年代にリチャード・E・ベルマンが最初に使いはじめ、1953年に現在の定義となった[1]。
効率のよいアルゴリズムの設計技法として知られる代表的な構造の一つである。対象となる問題を帰納的に解く場合にくり返し出現する小さな問題例について、解を表に記録し表を埋めていく形で計算をすすめ、冗長な計算をはぶくアルゴリズムのことをいう。特定のアルゴリズムを指すのではなく、上記のような手法を使うアルゴリズムの総称である。一般的に、帰納的な定義にしたがって再帰法でアルゴリズムを作ると計算結果の再利用は行わないが、入力が単純な構造で解が等しくなることの確認が容易であるとき、同じ入力について計算済であることの確認、結果の再利用をメモリ領域を消費して行い、計算を高速化する。初歩的な説明で使われるフィボナッチ数の計算、ハノイの塔の必要移動回数の計算などでは、一次元の表(列)によって指数オーダーの計算時間を入力の数の大きさに対して線形時間に落とすことができる。(ただし、これらの級数の計算では、漸化式で参照するのは高々 2 つ前の計算結果だけなので、変数を1, 2 個用意してループすればことたりる。)効果が顕著なのが組合せ問題で、文字列の近似照合(編集距離の計算)、ナップサック問題の解法などが、二次元の表により指数時間の手続きが多項式時間に効率化される有名な例である。マルチプルアラインメントのように表が三次元以上必要になると、時間に対するトレードオフとなるメモリ領域量が大きくなりすぎるため、規模の大きな入力には実用的でなくなる。
近似アルゴリズムの分野では、多項式時間での解法が存在しないと思われる一部の問題に対して、この方法を適用することで、擬似多項式時間では最適解を得ることができる。
実現方法
以下の2種類の実現方法がある。
- 履歴管理を用いるトップダウン方式(英: top-down with memoization) - 分割統治法において、計算結果を記録(メモ化)して再利用する方法。再帰を併用する場合はメモ化再帰(英: memoized recursion)とも呼ばれる。
- ボトムアップ方式(英: bottom-up method) - 先に部分問題を解いていく方法
適用条件
最適化問題に適用する場合、一般的に、以下の2つが適用する問題に成立していないといけない。(厳密には成立しなくても動的計画法の定義は満たせる)
- 部分構造最適性(英: optimal substructure)や最適性原理(英: principle of optimality)[2]
- 部分問題重複性(英: overlapping subproblems)
部分構造最適性とは、以下の2条件が成立していることをさす。
- 部分問題も同じ最適化問題が成立している
- 部分問題間が独立している
部分問題を解き、それを利用して、全体の最適化問題を解く戦略のため、部分構造最適性が動的計画法には必要である。部分構造最適性の例として、最短経路問題では、A → B → C という最短経路において、A → B や B → C も最短経路でないといけない(このことは背理法により証明可能)。また、部分問題間が独立であるためには、部分問題で資源の共有があってはならない。最短経路問題では A → B と B → C で同じ辺が出現しないため(同じく背理法により証明可能)、資源の共有が発生していない。貪欲法においても厳密解を求めるのなら部分構造最適性は必要である。
部分問題重複性とは、同一の部分問題が繰り返し出現することである。動的計画法では重複する部分問題の計算結果を記録し再利用する事により計算量を削減する。
厳密なことを書くと、全体問題と部分問題は完全に同一である必要性はなく、また、部分問題間が独立でなくても、それらが何らかの計算式により依存関係を解決し結合させる方法があれば、部分構造最適性が成立しなくても動的計画法の定義を満たすアルゴリズムは作れる。しかし、そのような実用例は少ない。
例題
動的計画法の適用例を示す。
フィボナッチ数列
フィボナッチ数列とは第 n 項の値が第 n - 1 項と第 n - 2 項の和となる数列のことである。この問題は最適化問題ではない。
定義を直接実装したプログラム
定義に基づいてプログラムを作成すると、次のようになる。
int fib(unsigned int n) {
switch (n) {
case 0: return 0;
case 1: return 1;
default: return fib(n - 1) + fib(n - 2);
}
}
例えば、このプログラムを使ってフィボナッチ数列の第5項を求める場合を考えてみる。このプログラムは再帰的に呼び出されるので、その様子を以下に示す。
fib(5) = fib(4) + fib(3) = (fib(3) + fib(2)) + (fib(2) + fib(1)) = ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1)) = (((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
このように最終的に fib(0) と fib(1) の呼び出しに収束し、fib(0) と fib(1) の呼び出し回数の和が結果の値となる。この方法を用いたフィボナッチ数列の計算量は 
| 一般 |
|
|---|---|
| 微分可能 |
|
| 凸縮小化 |
| ||||
|---|---|---|---|---|---|
| 線型 および 二次 |
|
| 系列範例 (Paradigms) | |||||
|---|---|---|---|---|---|
| グラフ理論 |
|
 は
は  を
を 
 が
が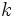 をもつときは
をもつときは 

