A New Simple Technique to Bootstrap Various Lattice Zero-Knowledge Proofs to QROM Secure NIZKs

Abstract

Many of the recent advanced lattice-based $\varSigma$-/public-coin honest verifier (HVZK) interactive protocols based on the techniques developed by Lyubashevsky (Asiacrypt’09, Eurocrypt’12) can be transformed into a non-interactive zero-knowledge (NIZK) proof in the random oracle model (ROM) using the Fiat-Shamir transform. Unfortunately, although they are known to be secure in the classical ROM, existing proof techniques are incapable of proving them secure in the quantum ROM (QROM). Alternatively, while we could instead rely on the Unruh transform (Eurocrypt’15), the resulting QROM secure NIZK will incur a large overhead compared to the underlying interactive protocol.

In this paper, we present a new simple semi-generic transform that compiles many existing lattice-based $\varSigma$-/public-coin HVZK interactive protocols into QROM secure NIZKs. Our transform builds on a new primitive called extractable linear homomorphic commitment protocol. The resulting NIZK has several appealing features: it is not only a proof of knowledge but also straight-line extractable; the proof overhead is smaller compared to the Unruh transform; it enjoys a relatively small reduction loss; and it requires minimal background on quantum computation. To illustrate the generality of our technique, we show how to transform the recent Bootle et al.’s 5-round protocol with an exact sound proof (Crypto’19) into a QROM secure NIZK by increasing the proof size by a factor of 2.6. This compares favorably to the Unruh transform that requires a factor of more than 50.

1 Introduction

The Fiat-Shamir transform [17] is one of the most popular methods to construct non-interactive zero-knowledge ($\mathsf{NIZK}$) proofs¹ in the random oracle model (ROM) based on a $\varSigma$-protocol (or more generally a public-coin honest-verifier zero-knowledge ($\mathsf{HVZK}$) interactive protocol). Due to the ever-growing risk of quantum computers, understanding the quantum security of $\mathsf{NIZK}\mathrm {s}$ in the quantum ROM [6] based on the Fiat-Shamir transform (or related transforms) have been considered to be an important research topic both in theory and practice. However, although many techniques in the QROM have accumulated in the last decade, including but not limited to [6, 7, 13, 14, 23, 25, 32,33,34, 37, 38], our understanding of $\mathsf{NIZK}\mathrm {s}$ in the QROM is still not as clear as those in the classical ROM. Notably, many of the recent lattice-based $\varSigma$-/public-coin $\mathsf{HVZK}$ interactive protocols, such as [1,2,3, 8, 15, 35], based on the techniques developed by Lyubashevsky [27, 28] fall into the following situations:

• they are not known to be (in)secure when applied the Fiat-Shamir transform in the QROM, and/or

• they can be transformed into a QROM secure $\mathsf{NIZK}$ using the Unruh transform [33] but incurs a large overhead, say at least $\times 50$, compared to the underlying interactive protocol.

Considering that we can securely apply the Fiat-Shamir transform to these protocols in the classical ROM to obtain efficient $\mathsf{NIZK}\mathrm {s}$, the current state-of-the-affair is unsatisfactory. Below, we briefly recall $\mathsf{NIZK}\mathrm {s}$ in the QROM.

QROM secure $\mathsf{NIZK}\mathrm {s}$ . Broadly speaking, there are two breeds of transformation to obtain QROM secure $\mathsf{NIZK}\mathrm {s}$ (that are a proof of knowledge) from a $\varSigma$-/public-coin $\mathsf{HVZK}$ interactive protocol. One is the Fiat-Shamir transform [17] and the other is the Unruh transform [33].

Recently, Don et al. [14] and Liu and Zhandry [25] showed how to argue security of the Fiat-Shamir transform in the QROM in two steps: they first showed that the Fiat-Shamir transform converts a standard $\varSigma$-protocol that is additionally a quantum proof of knowledge into an $\mathsf{NIZK}$ secure in the QROM, and then additionally showed how to construct a $\varSigma$-protocol that is a quantum proof of knowledge. Let us call such a $\varSigma$-protocol as a quantum secure $\varSigma$-protocol. It was shown in [25] (and partially in [14]) that Lyubashevsky’s $\varSigma$-protocol for proving possession of a short vector $\mathbf {e}$ such that $\mathbf {A}\mathbf {e}= \mathbf {u}$ is quantum secure for appropriate parameters. Concretely, by increasing the parameters compared to those required by the classically secure protocol, they showed that Lyubashevsky’s $\varSigma$-protocol has a “collapsing” property. However, such techniques for proving that a $\varSigma$-protocol is quantum secure are still limited and it seems non-trivial to generalize them to work for the recent more advanced lattice-based protocols. Moreover, these techniques that require rewinding quantum adversaries so far incur a large reduction loss of at least a factor $Q^{4t - 2}$, where Q is the number of adversarial random oracle queries and t is the number of valid transcripts required to invoke special soundness of the underlying $\varSigma$-protocol. Since setting the parameters without taking these huge reduction losses into consideration sometimes lead to concrete attacks [22, 24], having a tighter reduction is desirable.

On the other hand, Unruh [33] showed an elegant transform that converts any standard $\varSigma$-protocol into a QROM secure $\mathsf{NIZK}$. The benefit of the Unruh transform is that it works for any $\varSigma$-protocol, the reduction loss is tight, and it is also straight-line extractable.² The last strong property guarantees that the witness from a proof can be extracted without rewinding the adversary and is especially suitable for applications requiring multiple concurrent executions of $\mathsf{NIZK}\mathrm {s}$ such as group signatures [4] and anonymous attestations [9]. On the other hand, one of the main downsides is that it may incur a noticeable overhead in the proof size compared to the Fiat-Shamir transform since the transformation crucially relies on the challenge set being small. While the overhead can be reasonable when the underlying $\varSigma$-protocol already has a small challenge set, e.g., [10], it becomes prohibitively large as the challenge set grows. Recently, Chen et al. [11] extended the Unruh transform to work against a 5-round public-coin $\mathsf{HVZK}$ interactive protocol when restricting the second challenge to be binary.

Coming back to lattice-based ZK proofs. There are two main approaches in the current literature to construct lattice-based $\mathsf{NIZK}\mathrm {s}$. One builds on the Fiat-Shamir with abort paradigm developed by Lyubashevsky [27, 28] and the other builds on Stern’s protocol [21, 31]. While the QROM security of the latter approach is well understood since it has a simple combinatorial “commit-and-open” structure [13, 14], the QROM security of the former approach remains elusive. Notably, for the recent lattice-based protocols such as [1,2,3, 8, 15, 35], we either still do not know how to apply the Fiat-Shamir transform and/or require to pay a huge overhead when adopting the Unruh transform to argue QROM security. Therefore, a natural question is:

Can we generically and more efficiently transform lattice-based $\varSigma$-/public-coin $\mathsf{HVZK}$ interactive protocols based on the Fiat-Shamir with abort paradigm into QROM secure $\mathsf{NIZK}\mathrm {s}$ ?

Ultimately, we would like the transform to achieve the best of the two known transforms: to maintain similar proof size and soundness error of the underlying $\varSigma$-protocol like the Fiat-Shamir transform [17], while also providing a tight reduction along with a straight-line extractor like the Unruh transform [33].

1.1 Our Contribution

In this work, we provide partial affirmative answers to the above problem. We present a new simple semi-generic transform that compiles many existing lattice-based $\varSigma$-/public-coin $\mathsf{HVZK}$ interactive protocols such as [1, 3, 8, 15, 35] into a QROM secure NIZK that is also straight-line (simulation) extractable [16]. The proof overhead is smaller compared to the Unruh transform and enjoys a relatively small reduction loss. In many cases, the reduction loss only scales linearly with t (i.e., number of valid transcripts to invoke special soundness), rather than exponentially (e.g., $Q^{4t - 2}$) required by the Fiat-Shamir transform explained above. This is quite desirable since t can get quite large in recent advanced protocols; for instance [1] requires $t = 32$ in one of their settings, making the reduction loss as large as $2^{638}$ for a modest $Q = 2^{20}$.

As a concrete example, we show how to transform the recent Bootle et al.’s 5-round protocol with an exact sound proof [8] into a QROM secure $\mathsf{NIZK}$ by only increasing the proof size by a factor of 2.6.³ This is in contrast to using the recent extended Unruh transform [11]⁴, which increases the proof size by a larger factor of 51.8. Note that we are not aware of any method to securely apply the Fiat-Shamir transform to Bootle et al.’s protocol in the QROM. Finally, we highlight that not only our transform is very simple but the security proofs are also quite simple and involves a minimal amount of discussion regarding quantum computation.

Our contribution can be divided into the following steps. We only provide a high-level explanation of each step below and refer to Sect. 1.2 for a more detailed overview.

• 1. We first propose a new 3-round public-coin interactive protocol called extractable linear-homomorphic commitment ($\mathsf {LinHC}$) protocol. (See Sect. 3)

• 2. We then show how to bootstrap a broad class of $\varSigma$-protocols into a $\varSigma$-protocol that is also a quantum straight-line proof of knowledge by using an extractable $\mathsf {LinHC}$ protocol. Here, we consider the class of $\varSigma$-protocols where the response (i.e., the prover’s third message) is of the form $\mathbf {z}= \beta \cdot \mathbf {e}+ \mathbf {r}$, where $\mathbf {e}\in \mathbb {Z}_q^m$ is the witness, $\beta$ is the challenge sampled by the verifier, and $\mathbf {r}\in \mathbb {Z}_q^m$ is the masking term committed in the prover’s first message.⁵ (See Sect. 4.1)

• 3. We further show that we can apply the Fiat-Shamir transform to $\varSigma$-protocols with a quantum straight-line proof of knowledge to construct a QROM secure $\mathsf{NIZK}$ that is also straight-line extractable. (See Sect. 4.2)

• 4. We provide two simple constructions of lattice-based extractable $\mathsf {LinHC}$ protocols: one based on the module learning with errors ($\mathsf {MLWE}$) problem, and the other based on the $\mathsf {MLWE}$ and the decisional small matrix ratio ($\mathsf {DSMR}$) problem, where the latter is more efficient. Here the $\mathsf {DSMR}$ problem is a generalization of the decisional small polynomial ratio problem [26, 30] defined over a module NTRU lattice [12]. (See Sect. 3.4)

• 5. Finally, we discuss how to apply extractable $\mathsf {LinHC}$ protocols to more advanced lattice-based public-coin $\mathsf{HVZK}$ interactive protocols. As a concrete example, we provide the details on how to make Bootle et al.’s 5-round protocol with an exact sound proof [8] into a QROM secure $\mathsf{NIZK}$ with concrete parameters. We chose this protocol since it is one of the more complex protocols that have appeared in the literature while still being relatively simple enough to fit in our framework. We show how the ideas can be used to obtain similar results for other protocols such as [1, 3, 15, 35]. (See Sect. 5)

One notable difference between our transform and prior transforms that achieve straight-line extractable $\mathsf{NIZK}\mathrm {s}$ either in the classical or post-quantum setting (i.e., Fischlin [18] and Unruh [33]) is that ours do not put any restriction on the size of the challenge set of the underlying $\varSigma$-protocol. Therefore, if the underlying $\varSigma$-protocol has an exponentially large challenge set, we can use it directly to obtain an $\mathsf{NIZK}$, thus circumventing an inefficient soundness amplification required by prior transforms. We note that our result does not contradict the impossibility result of Fischlin [18] who (roughly) showed that an $\mathsf{NIZK}$ in the ROM with a straight-line extractor that cannot program the random oracle requires a prover to query the random oracle on at least $\omega (\log \kappa )$ points to produce a proof, where $\kappa$ is the security parameter. The main reason is that our $\mathsf{NIZK}$ requires the extractor to program the (Q)RO similar to the proof in the Fiat-Shamir transform. The difference between the Fiat-Shamir transform is that our extractor reprograms the (Q)RO in a way that it does not require to rewind the adversary to extract the witness.

Related works on $\varSigma$-protocols, $\mathsf{NIZK}\mathrm {s}$, and lattice-based ZK proofs and QROM secure signatures are provided in the full version.

1.2 Technical Overview

We provide an overview of each step explained in the above contribution.

Items 1 and 2: Extractable $\mathsf {LinHC}$ protocols and integrating it to $\varSigma$-protocols. We use Lyubashevsky’s $\varSigma$-protocol [27, 28], which we denote by $\varSigma _\mathsf {Lyu}$-protocol, as a leading example. It forms the basis of lattice-based zero-knowledge proofs based on the Fiat-Shamir with abort paradigm and the ideas presented below extend naturally to more advanced protocols.

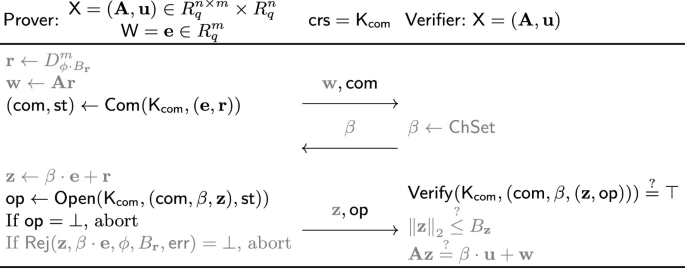
Let $\mathbf {A}\in R_q^{n \times m}$ and $\mathbf {u}\in R_q^n$ be public, where R and $R_q$ denote the rings $\mathbb {Z}[X]/(X^d + 1)$ and $\mathbb {Z}_q[X]/(X^d + 1)$. Then, the $\varSigma _\mathsf {Lyu}$-protocol allows one to prove knowledge of a short vector $\mathbf {e}\in R^m$ satisfying $\mathbf {A}\mathbf {e}= \mathbf {u}$.⁶ The prover first sends $\mathbf {w}= \mathbf {A}\mathbf {r}$ to the verifier where $\mathbf {r}\in R^m$ is a random short vector sampled from some specific distribution. The verifier returns a randomly sampled challenge $\beta \leftarrow \{ 0,1 \} ^d$, where $\beta$ is viewed as an element over R by the standard coefficient embedding. Finally, the prover sends $\mathbf {z}= \beta \cdot \mathbf {e}+ \mathbf {r}$ to the verifier. Here, it is standard to perform a rejection sampling step to make $\mathbf {z}$ statistically independent from $\mathbf {e}$. However, we ignore this subtle issue in the overview. Finally, the verifier accepts if $\mathbf {z}$ is short and $\mathbf {A}\mathbf {z}= \beta \cdot \mathbf {u}+ \mathbf {w}$ holds. It is known that the $\varSigma _\mathsf {Lyu}$-protocol satisfies relaxed (rather than exact) special soundness: Given two valid transcripts of the form $(\mathbf {w}, \beta , \mathbf {z})$ and $(\mathbf {w}, \beta ', \mathbf {z}')$ with $\beta \ne \beta '$, an extractor $\mathsf {Extract}_\mathsf{ss}$ outputs a witness $\mathbf {z}^* = \mathbf {z}- \mathbf {z}'$ such that $\mathbf {A}\mathbf {z}^* = (\beta - \beta ') \cdot \mathbf {u}$. Here, although $\mathbf {z}^*$ does not lie in the original relation, such proof of knowledge for a relaxed relation has proven to suffice in many applications.

  Our idea to turn the $\varSigma _\mathsf {Lyu}$-protocol to be a straight-line proof of knowledge is simple. Here, recall that to show a $\varSigma$-protocol is straight-line proof of knowledge, informally we need to construct an extractor $\mathsf {SL\text {-}Extract}$ that on input a single valid transcript (and some private information), outputs a witness $\mathbf {z}^*$. As a first step, we let the prover commit to its witness $\mathbf {e}$ and randomness $\mathbf {r}$ by a linear homomorphic commitment scheme. The prover outputs $\mathbf {w}= \mathbf {A}\mathbf {r}$ as in the original protocol along with two commitments $\mathsf {com} _\mathbf {e}= \mathsf {Com} _\mathsf{pk} (\mathbf {e})[\delta _\mathbf {e}]$ and $\mathsf {com} _\mathbf {r}= \mathsf {Com} _\mathsf{pk} (\mathbf {r})[ \delta _\mathbf {r}]$, where $\mathsf{pk}$ is a commitment key, and $\delta _\mathbf {e}$ and $\delta _\mathbf {r}$ are commitment randomness.⁷ Then, given a random challenge $\beta$ from the verifier, the prover returns $\mathbf {z}= \beta \cdot \mathbf {e}+\mathbf {r}$ and the commitment randomness $\delta _\mathbf {z}:= \beta \cdot \delta _\mathbf {e}+ \delta _\mathbf {r}$ as the third message. The verifier accepts if $\mathbf {z}$ is short; $\mathbf {A}\mathbf {z}= \beta \cdot \mathbf {u}+ \mathbf {w}$ holds; and $\mathsf {Com} _\mathsf{pk} (\mathbf {z})[ \delta _\mathbf {z}] = \beta \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r}$ holds. Here, for correctness to hold, we require the commitment scheme to satisfy linear homomorphism also over the randomness, i.e., $\beta \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r}= \mathsf {Com} _\mathsf{pk} (\beta \cdot \mathbf {e}+ \mathbf {r})[ \beta \cdot \delta _\mathbf {e}+ \delta _\mathbf {r}]$ for any $\beta \in \{ 0,1 \} ^d \subset R$.

We first check our modified $\varSigma _\mathsf {Lyu}$-protocol remains secure in the standard sense. Special soundness follows since two valid transcripts of the modified $\varSigma _\mathsf {Lyu}$-protocol include two valid transcripts of the original $\varSigma _\mathsf {Lyu}$-protocol. Next, assume $\delta _\mathbf {z}$ does not leak any information on the original commitment randomness $\delta _\mathbf {e}$ and $\delta _\mathbf {r}$. Then, (roughly) we can invoke the hiding property of the commitment scheme to argue that $\delta _\mathbf {z}$, $\mathsf {com} _\mathbf {e}$, and $\mathsf {com} _\mathbf {r}$ leak no information on $\mathbf {e}$ and $\mathbf {r}$ expect that they satisfy $\mathbf {z}=\beta \cdot \mathbf {e}+ \mathbf {r}$. Therefore, since the $\varSigma _\mathsf {Lyu}$-protocol is $\mathsf{HVZK}$, so is our modified $\varSigma _\mathsf {Lyu}$-protocol.

How to extract a witness. To show that it is a straight-line proof of knowledge, we enhance the linearly homomorphic commitment scheme to be extractable. Namely, we assume there exists an alternative key generation algorithm ${\mathsf {SimKeyGen}}$ that outputs a simulated commitment key ${{\mathsf {pk}^*}}$ with an associated trapdoor $\tau$ with the following properties: ${{\mathsf {pk}^*}}$ is indistinguishable from $\mathsf{pk}$ output by the honest key generation algorithm $\mathsf {KeyGen}$, and there exists a commitment extractor $\mathsf {Extract} _\mathsf {Com}$ such that on input the trapdoor $\tau$ and an honestly generated commitment $\mathsf {com} _\mathbf {x}= \mathsf {Com} _{{\mathsf {pk}^*}} (\mathbf {x})[ \delta _\mathbf {x}]$, outputs $\mathbf {x}$. Intuitively, it seems such an extractor $\mathsf {Extract} _\mathsf {Com}$ immediately implies a straight-line extractor $\mathsf {SL\text {-}Extract}$. On input a valid transcript $( (\mathbf {w}, \mathsf {com} _\mathbf {e}, \mathsf {com} _\mathbf {r}), \beta , (\mathbf {z}, \delta _\mathbf {z}) )$, $\mathsf {SL\text {-}Extract}$ just runs $\mathbf {e}\leftarrow \mathsf {Extract} _\mathsf {Com} (\tau , \mathsf {com} _\mathbf {e})$ to extract the witness $\mathbf {e}$. However, this intuition is clearly wrong since an adversary might have constructed a malformed commitment $\mathsf {com} _\mathbf {e}$ and $\mathsf {com} _\mathbf {r}$ that satisfies $\mathsf {Com} _{{\mathsf {pk}^*}} (\mathbf {z})[\delta _\mathbf {z}] =\beta \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r}$. Notably, the only commitment $\mathsf {SL\text {-}Extract}$ sees that is guaranteed to be valid is $\beta \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r}$ due to correctness. However, since $\mathsf {SL\text {-}Extract}$ already knows that this opens to $\mathbf {z}$, there seems to be no point using the trapdoor $\tau$.

The main observation here is that since the adversary must prepare $\mathsf {com} _\mathbf {e}$ and $\mathsf {com} _\mathbf {r}$ before seeing the challenge $\beta$, there should be several other $\beta$’s in $\{ 0,1 \} ^d$ that it would have been able to produce valid openings to. To make the discussion simple, we first assume the case where the challenge space of the $\varSigma _\mathsf {Lyu}$-protocol is only of polynomial size and the existence of another valid commitment $\beta ' \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r}$ with $\beta ' \ne \beta$ is guaranteed. Then, $\mathsf {SL\text {-}Extract}$ runs through all $\beta \in \{ 0,1 \} ^d$ and executes $\mathsf {Extract} _\mathsf {Com} ( \tau ,\beta \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r})$ in polynomial time. Since $\beta ' \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r}$ is guaranteed to be a valid commitment, $\mathsf {Extract} _\mathsf {Com}$ outputs the corresponding message $\mathbf {z}'$ committed to $\beta ' \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r}$. After finding such $\mathbf {z}'$, $\mathsf {SL\text {-}Extract}$ can invoke the special soundness extractor $\mathsf {Extract}_\mathsf{ss}$ on input $(\mathbf {w}, \beta , \beta ', \mathbf {z}, \mathbf {z}')$ to obtain a witness $\mathbf {z}^*$ for the (relaxed) relation. We can turn this rough idea into a formal proof by performing parallel repetition of the $\varSigma _\mathsf {Lyu}$-protocol to amplify the soundness error to be negligible while noticing that $\mathsf {SL\text {-}Extract}$ still only needs to invoke $\mathsf {Extract} _\mathsf {Com}$ a polynomial time. However, recall the goal was to extract without having to restrict the challenge space of the $\varSigma _\mathsf {Lyu}$-protocol to be polynomial size as required by the Fischlin and Unruh transforms [18, 33].⁸

Making the challenge set exponentially large. By slightly refining the above argument, we can make sure the above idea works even when the challenge set is exponentially large. Assume an adversary has a non-negligible probability $\epsilon$ in completing the $\varSigma _\mathsf {Lyu}$-protocol with an honest verifier. Then conditioning on the adversary succeeding, a standard statistical argument shows that with probability at least 1/2, the adversary must have been able to output a valid response for at least $\epsilon$-fraction of the challenges. That is, there exists $2^d \cdot \epsilon$ other $\beta$’s in $\{ 0,1 \} ^d$ that the adversary was able to output a valid third message $(\mathbf {z}, \delta _\mathbf {z})$. Therefore, we define the $\mathsf {SL\text {-}Extract}$ to execute $\mathsf {Extract} _\mathsf {Com} ( \tau , \beta \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r})$ on roughly $(\kappa / \epsilon )$-randomly chosen $\beta$’s. Then, with probability at least $1- 2^{-\kappa }$, $\mathsf {SL\text {-}Extract}$ finds the desired $\mathbf {z}'$ and the rest follows the same argument made above.

Since the above argument is purely statistical and agnostic to whether the adversary is classical or quantum, the resulting modified $\varSigma _\mathsf {Lyu}$-protocol is by default a quantum straight-line proof of knowledge. In Sect. 3, we formalize the properties required by the underling commitment scheme and define it as a new interactive protocol called the extractable linear homomorphic commitment ($\mathsf {LinHC}$) protocol. We note that the extractable $\mathsf {LinHC}$ protocol can be naturally plugged into multi-round public-coin $\mathsf{HVZK}$ interactive protocols with similar structures. Finally, an acute reader may have noticed that our resulting $\varSigma$-protocol is in the common reference string (CRS) model since it requires a commitment key $\mathsf{pk}$. Although this is true in general, for our specific extractable $\mathsf {LinHC}$ protocol, the $\mathsf{pk}$ can be the output of the (Q)RO on any input of the prover’s choice so the resulting $\varSigma$-protocol will not require any CRS.

Item 3: Applying the Fiat-Shamir transform in the QROM. A quantum straight-line extractable $\varSigma$-protocol is particularly quantum secure so we can appeal to recent techniques [14, 25] to transform it into a QROM secure $\mathsf{NIZK}$ or a QROM secure signature. However, we can take advantage of the straight-line extractability of the $\varSigma$-protocol to provide simpler and tighter proofs. Recall one of the main reasons that made the proof of Fiat-Shamir transform in the QROM difficult when basing on standard $\varSigma$-protocols was that there was no easy way to extract a witness from a forged proof output by the adversary. Therefore, by using the straight-line extractor $\mathsf {SL\text {-}Extract}$ to extract from the forged proof, it seems we can overcome one of the most difficult obstacles. We outline the proof and explain some of the pitfalls. As commonly done in the literature, below we consider the proof for the deterministic signature scheme based on the Fiat-Shamir transform (which captures the essence of a simulation sound/extractable $\mathsf{NIZK}$).⁹

Proof overview. The proof consists of two parts: first show that if the signature scheme is unforgeable against no-message attack ($\mathsf {UF\text {-}NMA}$) secure, then it is secure in the standard sense, i.e., unforgeable against chosen message attack ($\mathsf {UF\text {-}CMA}$) secure; next, show that if the relation used by the $\varSigma$-protocol is hard, then the signature scheme is $\mathsf {UF\text {-}NMA}$ secure. Here, recall $\mathsf {UF\text {-}NMA}$ considers the setting where an adversary is not allowed to make any signing queries.

  The first part of the proof follows closely to those given by Kiltz et al. [23] (which themselves follow [33, 34]) who showed quantum security of a Fiat-Shamir transformed signature scheme basing on a special type of $\varSigma$-protocol (or more specifically a lossy identification protocol). The main observation is that by using the $\mathsf{HVZK}$ simulator of the $\varSigma$-protocol, we can make the proof history-free [6]. In particular, for each message $\mathsf {M}$, we deterministically generate a transcript $(\mathbf {w}_\mathsf {M}, \beta _\mathsf {M}, \mathbf {z}_\mathsf {M})$ of the $\varSigma$-protocol using the $\mathsf{HVZK}$ simulator run on message-dependent randomness. Since the simulated transcript is determined uniquely by the message, we can program the random oracle $\mathsf {H}$ at the beginning of the game before invoking the adversary so that $\mathsf {H} (\mathbf {w}\Vert \mathsf {M})$ outputs $\beta _\mathsf {M}$ if and only if $\mathbf {w}= \mathbf {w}_\mathsf {M}$. Then, to answer a signature query, the simulator can output the already programmed simulated proof as the signature.

This high-level approach works for Kiltz et al. [23] without complications, however, we encountered a slight issue in our setting. The main difference is that while the $\varSigma$-protocol of Kiltz et al. satisfied statistical $\mathsf{HVZK}$, ours is only computational $\mathsf{HVZK}$. Concretely, for our specific instantiation of the extractable $\mathsf {LinHC}$ protocol based on the $\mathsf {MLWE}$ assumption, we informally need to argue that a superposition of the $\mathsf {MLWE}$ samples of the form , where $\mathbf {s}_{\mathsf {M}}, \mathbf {s}'_{\mathsf {M}}$ are random $\mathsf {MLWE}$ secrets, is indistinguishable from , where $\mathbf {b}_{\mathbf {s}_\mathsf {M}, \mathbf {s}'_\mathsf {M}}$ is a random vector. Unfortunately, we were not able to reduce the standard $\mathsf {MLWE}$ assumption to such an assumption. Here, roughly, $\mathbf {B}$ corresponds to the commitment key of the extractable $\mathsf {LinHC}$ protocol and each $\mathbf {B}\cdot \mathbf {s}_{\mathsf {M}} + \mathbf {s}'_{\mathsf {M}}$ corresponds to the commitment.

To resolve this issue, we tweak the extractable $\mathsf {LinHC}$ protocol to use fresh commitment keys $\mathbf {B}_\mathsf {M}$ for each message $\mathsf {M}$ and provide a slightly more general definition than what we laid out above. In particular, the extractable $\mathsf {LinHC}$ protocol we require to construct a QROM secure $\mathsf{NIZK}$/signature needs to have a more general structure compared to those required to construct a $\varSigma$-protocol with a quantum proof of knowledge. In Sect. 3, the latter is referred to as the “simplified” definition. Here, if we only care about the classical setting, then this issue does not appear so we can always rely on the simplified definition for both cases.

  The remaining piece is to show that we can extract a witness from the forgery output by the adversary. The reduction is the same as before: provided a forgery, the extractor probes many challenges $\beta$ randomly until $\mathsf {Extract} _\mathsf {Com} ( \tau ,\beta \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r})$ outputs a valid $\mathbf {z}$, where $\mathsf {com} _\mathbf {e}$ and $\mathsf {com} _\mathbf {r}$ are the commitments of the extractable $\mathsf {LinHC}$ protocol included in the adversary’s forgery. The main difference is in the analysis of the success probability of such a procedure. Since $\beta$ is generated as $\mathsf {H} ( \cdots \Vert \mathsf {com} _\mathbf {e}\Vert \mathsf {com} _\mathbf {r})$ when applying the Fiat-Shamir transform, the adversary has some control over the $\beta$ it uses. To make matters worse, it can make quantum queries to $\mathsf {H}$ to obtain a superposition of challenges . Therefore, we can no longer rely on the simple statistical argument that relied on $\beta$ being uniformly random. We will show how to upper bound the number of random sampling the extractor must perform before finding a “good” challenge $\beta$ by using bounds on the generic quantum search problem [20, 23, 36].

Item 4: Constructing extractable $\mathsf {LinHC}$ protocols. It remains to show how to construct an extractable $\mathsf {LinHC}$ protocol based on lattices. The construction is a simple variant of the (dual) Regev public-key encryption scheme [19, 29] that is known to be linearly homomorphic. The commitment key is two random matrices $\mathsf{pk} = (\mathbf {A}, \mathbf {B}) \in R_q^{m \times n} \times R_q^{m \times n}$ and commitments to the short vectors $(\mathbf {e}, \mathbf {r}) \in R^m_q \times R^m_q$ are defined as follows for :

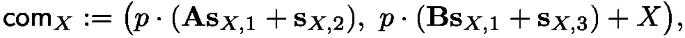
where p is some odd integer coprime to q and the $\mathbf {s}$’s are commitment randomness sampled from an appropriate domain. Then, for any challenge $\beta \in \{ 0,1 \} ^d \subset R$, we can construct a commitment to $\mathbf {z}= \beta \cdot \mathbf {e}+ \mathbf {r}$ by computing $\mathsf {com} _\mathbf {z}= \beta \cdot \mathsf {com} _\mathbf {e}+ \mathsf {com} _\mathbf {r}$, which is again of the form $\mathsf {com} _\mathbf {z}= \big ( p \cdot (\mathbf {A}\mathbf {s}_{\mathbf {z}, 1} + \mathbf {s}_{\mathbf {z}, 2}), ~p \cdot (\mathbf {B}\mathbf {s}_{\mathbf {z}, 1} + \mathbf {s}_{\mathbf {z}, 3}) + \mathbf {z} \big )$, where $\mathbf {s}_{\mathbf {z}, i} = \beta \cdot \mathbf {s}_{\mathbf {e}, i} + \mathbf {s}_{\mathbf {r}, i}$ for $i \in [3]$. However, we cannot simply output the tuple $( \mathbf {s}_{\mathbf {z},i} )_{i \in [3]}$ as the opening of $\mathsf {com} _\mathbf {z}$ to the message $\mathbf {z}$ since $\mathbf {s}_{\mathbf {z}, i}$ may leak information of $\mathbf {s}_{\mathbf {e}, i}$ and $\mathbf {s}_{\mathbf {r}, i}$. Instead, we use the rejection sampling technique [27, 28] and sample each $\mathbf {s}_{\mathbf {r}, i}$ for $i \in [3]$ from a slightly wider distribution compared to those of the $\mathbf {s}_{\mathbf {e}, i}$’s and only output the tuple $( \mathbf {s}_{\mathbf {z},i} )_{i \in [3]}$ with some fixed probability.¹⁰ Effectively, the opening $( \mathbf {s}_{\mathbf {z},i} )_{i \in [3]}$ are independent of the $\mathbf {s}_{\mathbf {e}, i}$’s. At this point, we can argue $\mathsf {com} _\mathbf {e}$ is indistinguishable from random by invoking the $\mathsf {MLWE}$ assumption. Moreover, since $\mathsf {com} _\mathbf {r}= \mathsf {com} _\mathbf {z}- \beta \cdot \mathsf {com} _\mathbf {e}$, we conclude that we can simulate $\mathsf {com} _\mathbf {r}$, $\mathsf {com} _\mathbf {e}$, and $( \mathbf {s}_{\mathbf {z},i} )_{i \in [3]}$ only using $\mathbf {z}= \beta \cdot \mathbf {e}+ \mathbf {r}$. Finally, extractability follows by switching the commitment key $\mathsf{pk}$ to be the real public-key of the encryption scheme. We set ${{\mathsf {pk}^*}} = (\mathbf {A}, \mathbf {B})$, where $\mathbf {B}= \mathbf {D}_1 \mathbf {A}+ \mathbf {D}_2$ for two matrices $\mathbf {D}_1$ and $\mathbf {D}_2$ with small entries. Then, for an appropriate set of parameters, given $\mathsf {com} _\mathbf {z}= (\mathbf {t}_1, \mathbf {t}_2)$, we can decrypt it by $(\mathbf {t}_2 - \mathbf {D}_1 \mathbf {t}_1) \mod p = \mathbf {z}$.

Item 5: A concrete example. Finally, we provide a more interesting use-case for our extractable $\mathsf {LinHC}$ protocol other than the Lyubashevsky’s $\varSigma$-protocol explained above. We consider the 5-round public-coin $\mathsf{HVZK}$ interactive protocol by Bootle et al. [8] that achieves exact special soundness. So far, we do not know how to apply the Fiat-Shamir transform securely in the QROM to this protocol since unlike the Lyubashevsky’s $\varSigma$-protocol, there is no natural notion of “collapsingness” [14, 25]. We can instead try applying the recent Unruh transform extended to 5-round protocols by Chen et al. [11] by limiting the second challenge used by the verifier to be binary. For completeness, we show in the full version that assuming the extended Unruh transform applies to Bootle et al.’s protocol, we incur a factor 51.8 blowup in the proof size. In Sect. 5, we show that our extractable $\mathsf {LinHC}$ works simply as a wrapper and bootstraps the original protocol of Bootle et al. to be quantum secure with an overhead of only a factor 2.6. We also discuss how the same ideas are applicable to other lattice-based protocols such as [1, 3, 15, 35]. As the main focus of this study is to introduce new theoretical tools and ideas to transform $\varSigma$-protocols into QROM secure $\mathsf{NIZK}\mathrm {s}$, we leave optimization and assessment of the concrete security of other lattice-based protocols as future work. Finally, we note that applying our extractable $\mathsf {LinHC}$ on Lyubashevsky’s $\varSigma$-protocol does not result in a more efficient QROM secure signature scheme compared to the QROM secure Dilithium proposed in [23]. Roughly, this is because when viewed as an $\mathsf{NIZK}$, ours achieve a stronger property: while [23] only achieves soundness, we also achieve (straight-line) proof of knowledge.

2 Preliminary

The notations we use in this paper and a minimal set of tools on quantum computation in provided in the full version.

2.1 $\varSigma$-Protocol

We use the standard notion of $\varSigma$-protocol in the common reference string model.¹¹ We note that it is standard in lattice-based protocols to consider non-abort honest-verifier zero-knowledge ($\mathsf{naHVZK}$), where the ZK simulator is only required to simulate non-aborting transcripts. Due to page limitation, we refer the basic definitions to the full version and only provide the definition of straight-line proof of knowledge below.

Definition 2.1

(Straight-line proof of knowledge). A $\varSigma$-protocol has a (quantum) $\epsilon _{\mathsf {IndO}}$-straight-line proof of knowledge ($\mathsf {SL\text {-}PoK}$) if there exists a PPT simulator $\mathsf {SimSetup}$ and a PPT straight-line extractor $\mathsf {SL\text {-}Extract}$ with the following properties:

• For any QPT $\mathcal {A}$, the advantage $\mathsf {Adv}^{\mathsf {IndCRS}}(\mathcal {A})$ defined below is less than $\epsilon _\mathsf {IndCRS}$: $\mathsf {Adv}^{\mathsf {IndCRS}}(\mathcal {A}) :=| \Pr [ \mathsf {crs} \leftarrow \mathsf{Setup} (1^\kappa ): \mathcal {A} (1^\kappa , \mathsf {crs}) \rightarrow 1] - \Pr [ (\widetilde{\mathsf {crs}}, \tau ) \leftarrow \mathsf {SimSetup} (1^\kappa ): \mathcal {A} (1^\kappa , \widetilde{\mathsf {crs}}) \rightarrow 1] |.$

• For any QPT $\mathcal {A}$ and any $\mathsf {X} \in \mathcal {L}$ satisfying

  

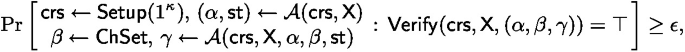
  we have

  

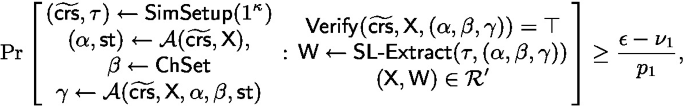
  for some polynomial $p_1$ and negligible function $\nu _1$. Moreover, the runtime of $\mathsf {SL\text {-}Extract}$ is upper bounded by $p_2 \cdot \big ( \frac{\epsilon - \nu _2}{p_3} - \frac{1}{\left| \mathsf { ChSet} \right| } \big )^{-1}$ for some polynomials $p_2, p_3$ and negligible function $\nu _2$.¹² Concretely, if $\epsilon$ is non-negligible and $\left| \mathsf { ChSet} \right|$ is super-polynomially large, then $\mathsf {SL\text {-}Extract}$ runs in polynomial time.

2.2 Lattices

Basic notations and well known tools for lattices are provided in the full version. We let $S_\eta$ denote the set of all elements in $a \in R_q$ such that ${\Vert w \Vert }_\infty \le \eta$. As with all $\varSigma$-protocols that rely on the Fiat-Shamir with abort technique, we use the rejection sampling technique [27, 28]. We denote the rejection sampling algorithm as $\mathsf {Rej}$. To construct extractable $\mathsf {LinHC}$ protocols, we rely on a variant of the standard module learning with errors $\mathsf {MLWE}$ assumption, where the adversary is allowed to obtain a superposition of independent $\mathsf {MLWE}$ samples (which remains as hard as the standard $\mathsf {MLWE}$ assumption). We also consider the quantum accessible decisional small matrix ratio ($\mathsf {DSMR}$) assumption, which is essentially the underlying hardness assumption of (module) NTRU.

3 Extractable Linear Homomorphic Commitment Protocol

In this section, we introduce a new interactive protocol called the extractable linear homomorphic commitment ($\mathsf {LinHC}$) protocol. We first provide the definition of an extractable $\mathsf {LinHC}$ protocol and then give two instantiations: one from the $\mathsf {MLWE}$ assumption and the other from the $\mathsf {MLWE}$ and the $\mathsf {DSMR}$ assumption. Below whenever we say $\varSigma$-protocols, the readers may safely replace them by public-coin $\mathsf{HVZK}$ non-interactive protocols.

We first define extractable $\mathsf {LinHC}$ protocol in its most general form and provide a simplified variant in the subsequent section. As explained in the introduction, the general definition, which is defined in the QROM, is useful when directly constructing (straight-line simulation extractable) $\mathsf{NIZK}\mathrm {s}$¹³ in the QROM from a possibly non-quantum secure $\varSigma$-protocol (see Sect. 4.2). In contrast, the simplified definition, which is defined in the standard model, is useful when constructing a quantum straight-line proof of knowledge $\varSigma$-protocol from a non-quantum secure $\varSigma$-protocol (see Sect. 4.1).

3.1 Definition

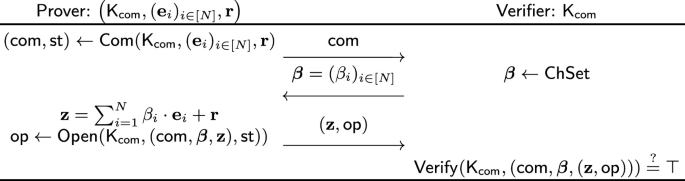
An illustration of the extractable $\mathsf {LinHC}$ protocol is provided in Fig. 1. Looking ahead, in the context of $\varSigma$-protocols, the $\mathbf {e}_i$’s and $\mathbf {r}$ correspond to the witness and commitment randomness (or masking term), respectively.

Fig. 1.

An extractable linear homomorphic commitment protocol. $\mathsf {K}_\mathsf{com}$ is a commitment key generated by $\mathsf {KeyGen} ^{\mathsf {H}}(1^\kappa )$, where $\mathsf {H}$ is modeled as a random oracle.

Definition 3.1

(Extractable linear homomorphic commitment protocol in QROM). An extractable linear homomorphic commitment ($\mathsf {LinHC}$) protocol is a three-round public-coin interactive protocol run between two parties (prover and verifier), and is defined by a tuple of PPT algorithms $\varPi _\mathsf {LinHC} = (\mathsf {KeyGen}, \mathsf {Com}, \mathsf {Open}, \mathsf{Verify})$ and a challenge set $\mathsf { ChSet} \subseteq (R_q)^N$. The protocol procedure is as follows:

• 1. A random oracle $\mathsf {H}$ is chosen and the key generation algorithm is executed $\mathsf {K}_\mathsf{com} \leftarrow \mathsf {KeyGen} ^\mathsf {H} ( 1^\kappa )$. Here, let $\{ 0,1 \} ^\nu$ be the randomness space used by $\mathsf {KeyGen}$;

• 2. The prover on input vectors $(( \mathbf {e}_i )_{i \in [N]}, \mathbf {r}) \in (R_q^m)^N \times R_q^m$, runs the commitment algorithm $(\mathsf {com}, \mathsf {st}) \leftarrow \mathsf {Com} (\mathsf {K}_\mathsf{com}, ( \mathbf {e}_i )_{i \in [N]}, \mathbf {r})$, and sends the first message $\mathsf {com}$ to the verifier;

• 3. The verifier samples a random challenge $\boldsymbol{\beta }\leftarrow \mathsf { ChSet}$ and sends the second message $\boldsymbol{\beta }$ to the prover;

• 4. The prover computes $\mathbf {z}\leftarrow \sum ^N_{i = 1} \beta _i \cdot \mathbf {e}_i + \mathbf {r}$¹⁴, runs the opening algorithm $\mathsf {op} \leftarrow \mathsf {Open} ( \mathsf {K}_\mathsf{com}, (\mathsf {com}, \boldsymbol{\beta }, \mathbf {z}), \mathsf {st})$, and sends the third message $(\mathbf {z}, \mathsf {op})$ to the verifier. We allow $\mathsf {op} = \bot$ for a special symbol $\bot$ to indicate failure;

• 5. The verifier returns the output of the deterministic verification algorithm $\mathsf{Verify} ( \mathsf {K}_\mathsf{com}, ( \mathsf {com}, \boldsymbol{\beta }, (\mathbf {z}, \mathsf {op})) )$, where $\top$ indicates accept and $\bot$ indicates reject. We call $(\mathsf {com}, \boldsymbol{\beta }, (\mathbf {z}, \mathsf {op}))$ the transcript and call $(\mathsf {com}, \boldsymbol{\beta }, \mathsf {op})$ a valid opening for $\mathbf {z}$ if the verifier accepts.

We require the following properties to hold.

Definition 3.2

(Correctness). An extractable linear homomorphic commitment protocol $\varPi _\mathsf {LinHC}$ has correctness error $(\delta _0, \delta _1)$ if for any choice of random oracle $\mathsf {H}$, $\mathsf {K}_\mathsf{com} \in \mathsf {KeyGen} ^\mathsf {H} (1^\kappa )$, and $(( \mathbf {e}_i )_{i \in [N]}, \mathbf {r}) \in (R_q^m)^N \times R_q^m$ the following holds:

• We have $\Pr [ \mathsf{Verify} ( \mathsf {K}_\mathsf{com}, (\mathsf {com}, \boldsymbol{\beta }, (\mathbf {z}, \mathsf {op}))) = \top ] \ge 1 - \delta _1$, where the probability is taken over the randomness to sample $(\mathsf {com}, \mathsf {st}) \leftarrow \mathsf {Com} (\mathsf {K}_\mathsf{com}, ( \mathbf {e}_i )_{i \in [N]}, \mathbf {r})$, $\boldsymbol{\beta }\leftarrow \mathsf { ChSet}$, and $\mathsf {op} \leftarrow \mathsf {Open} (\mathsf {K}_\mathsf{com}, (\mathsf {com}, \boldsymbol{\beta }, \sum ^N_{i = 1} \beta _i \cdot \mathbf {e}_i + \mathbf {r}), \mathsf {st})$ conditioned on $\mathsf {op} \ne \bot$.

• The probability that an honestly generated transcript $( \mathsf {com}, \boldsymbol{\beta }, (\mathbf {z}, \mathsf {op}) )$ contains $\mathsf {op} = \bot$ is bounded by $\delta _1$. In particular, $\Pr [ \mathsf {op} = \bot ] \le \delta _1$ where the probability is taken over the random coins of the prover and verifier.

Zero-knowledge. At a high level, zero-knowledge for an extractable $\mathsf {LinHC}$ protocol stipulates that the transcript should leak no information of the vectors $( \mathbf {e}_i )_{i \in [N]}$ and $\mathbf {r}$ other than the fact that it adds up to $\mathbf {z}$. Below, we provide a definition of zero-knowledge where an adversary can obtain superpositions of simulated proofs. Since $( \mathbf {e}_i )_{i \in [N]}$ corresponds to the witness of the underlying $\varSigma$-protocol, it will be reused many times. On the other hand, $\mathbf {r}$ is the commitment randomness that is freshly sampled for each transcript. This is reflected in the following definition by fixing $( \mathbf {e}_i )_{i \in [N]}$ and sampling fresh $\mathbf {r}$ (and challenge $\boldsymbol{\beta }$) using the distribution $D_{\boldsymbol{\beta }, \mathbf {r}}$. Also, one can think of each $\rho$ in the definition as a specific tag to distinguish each transcripts. Below, we say it is “semi”-honest-verifier since $\boldsymbol{\beta }$ does not necessarily need to be uniformly distributed over $\mathsf { ChSet}$.

Definition 3.3

(Quantum accessible no-abort (semi-)honest-verifier zero-knowledge). Let $D_{\boldsymbol{\beta }, \mathbf {r}}$ be any distribution over $\mathsf { ChSet} \times R_q^m$. For an oracle $\mathsf {H}$ and algorithm $\mathsf {ZKSim}$, define the following algorithms:

• $D^{\not \perp }_\mathsf {trans} (\rho , ( \mathbf {e}_i )_{i \in [N]}):$ On input $\rho \in \{ 0,1 \} ^\nu$ and $( \mathbf {e}_i )_{i \in [N]} \in (R_q^m)^N$, generate $\mathsf {K}_\mathsf{com} \leftarrow \mathsf {KeyGen} ^\mathsf {H} ( 1^\kappa )[\rho ]$ and sample $(\boldsymbol{\beta }, \mathbf {r}) \leftarrow D_{\boldsymbol{\beta }, \mathbf {r}}$. Then run an honest protocol with prover input $(\mathsf {K}_\mathsf{com}, (( \mathbf {e}_i )_{i \in [N]}, \mathbf {r}))$ conditioned on the verifier message being $\boldsymbol{\beta }$ and $\mathsf {op} \ne \bot$ (i.e., a non-aborting protocol). Finally, output $\mathbf {r}$ along with the valid transcript $(\mathbf {r}, \mathsf {trans} = (\mathsf {com}, \boldsymbol{\beta }, (\mathbf {z}, \mathsf {op})))$.

• $D_\mathsf {sim} (\rho , ( \mathbf {e}_i )_{i \in [N]}):$ On input $\rho \in \{ 0,1 \} ^\nu$ and $( \mathbf {e}_i )_{i \in [N]} \in (R_q^m)^N$, generate $\mathsf {K}_\mathsf{com} \leftarrow \mathsf {KeyGen} ^\mathsf {H} ( 1^\kappa )[\rho ]$, sample $(\boldsymbol{\beta }, \mathbf {r}) \leftarrow D_{\boldsymbol{\beta }, \mathbf {r}}$, and compute $\mathbf {z}\leftarrow \sum ^N_{i = 1} \beta _i \cdot \mathbf {e}_{i} + \mathbf {r}$. Then, run $(\mathsf {com}, \mathsf {op}) \leftarrow \mathsf {ZKSim} (\mathsf {K}_\mathsf{com}, \boldsymbol{\beta }, \mathbf {z})$ and output $(\mathbf {r}, \mathsf {trans} = (\mathsf {com}, \boldsymbol{\beta }, (\mathbf {z}, \mathsf {op})))$.

In above, we assume $D^{\not \perp }_\mathsf {trans}$ and $D_\mathsf {sim}$ run on a uniform and independent randomness for each input $\rho \in \{ 0,1 \} ^\nu$ and reuse the same randomness when run again on the same $\rho$.

Then, we say an extractable linear homomorphic commitment protocol $\varPi _\mathsf {LinHC}$ has $\epsilon _\mathsf {zk}$-quantum accessible no-abort (semi-)honest-verifier zero-knowledge, if there exists a PPT algorithm $\mathsf {ZKSim}$ such that for any $( \mathbf {e}_i )_{i \in [N]} \in (R_q^m)^N$, distribution $D_{\boldsymbol{\beta }, \mathbf {r}}$, and QPT $\mathcal {A}$, the advantage $\mathsf {Adv}^{\mathsf{QAnaHVZK}}(\mathcal {A})$ defined below is less than $\epsilon _\mathsf {zk}$:

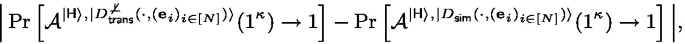
where the probability is also taken over the random choice of the random oracle $\mathsf {H}$.

Extractability. When considering extractable $\mathsf {LinHC}$ protocol as a tool to be integrated into a preexisting $\varSigma$-protocol, the third message $\mathbf {z}$ corresponds to the third message (usually referred to as the “response”) of the $\varSigma$-protocol. See Fig. 4 for an illustrative example. In particular, the verifier will always perform an additional check $f(\boldsymbol{\beta }, \mathbf {z}) {\mathop {=}\limits ^{\mathrm {?}}}\top$, where f is some function defined by the verifier algorithm of the underlying $\varSigma$-protocol. Therefore, for an extractable $\mathsf {LinHC}$ to be useful in the context of $\varSigma$ protocols, we want it to be able to extract valid tuples such that $f(\boldsymbol{\beta }_i, \mathbf {z}_i) = \top$ without rewinding the adversary only given an accepting transcript. After such k tuples are collected, we can invoke the k-special soundness extractor of the underlying $\varSigma$-protocol to extract a witness. More formally, we require the following.

Definition 3.4

($\mathcal {F}$-Almost straight-line extractable). Let $\mathcal {X}$ and $\mathcal {Y}$ be the input and output space required by the random oracle $\mathsf {H}$. An extractable linear homomorphic commitment protocol $\varPi _\mathsf {LinHC}$ is $\epsilon _{\mathsf {IndO}}$-$\mathcal {F}$-almost straight-line extractable for a function family $\mathcal {F}$ if there exists PPT algorithms $\mathsf {SimOracle}$ and $\mathsf {LinCExtract}$ with the following properties:

• 1. For any QPT $\mathcal {A}$, the advantage $\mathsf {Adv}^{\mathsf {IndO}}(\mathcal {A})$ defined below is less than $\epsilon _{\mathsf {IndO}}$:

  

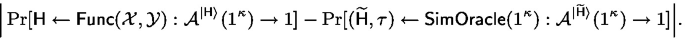
• 2. For any $(\widetilde{\mathsf {H}}, \tau ) \in \mathsf {SimOracle} (1^\kappa )$, randomness $\rho \in \{ 0,1 \} ^\nu$, first message $\mathsf {com}$, and any efficiently computable function $f \in \mathcal {F}$ with binary output , define the set $S_f(\rho , \mathsf {com})$ as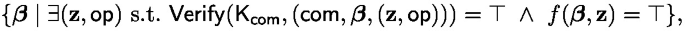

  

  where $\mathsf {K}_\mathsf{com} = \mathsf {KeyGen} ^{\widetilde{\mathsf {H}}}(1^\kappa )[ \rho ]$. Let $\delta , k$ be any positive integers such that $k < | S_f(\rho , \mathsf {com}) |$, and denote $T^* = \frac{k \cdot \delta \cdot \left| \mathsf { ChSet} \right| }{\left| S_f(\rho , \mathsf {com}) \right| - k}$. Then, on input a valid transcript $\mathsf {trans} = (\mathsf {com}, \boldsymbol{\beta }, (\mathbf {z}, \mathsf {op}))$, the linear commitment extractor $\mathsf {LinCExtract} (\tau , \rho , \mathsf {trans})$ outputs either a set 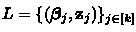or $\bot$ in time $T^* \cdot \mathsf {poly}(\kappa )$ for some fixed polynomial $\mathsf {poly}(\kappa )$, where all the $\boldsymbol{\beta }_j$’s in L are pairwise distinct and satisfies $f(\boldsymbol{\beta }_j, \mathbf {z}_j) = \top$. Moreover, the probability that it outputs L is at least $1- k \cdot 2^{-\delta }$. Concretely, when k is a constant, $\delta = \kappa$, and $\left| S_f(\rho , \mathsf {com}) \right| = \left| \mathsf { ChSet} \right| \cdot \epsilon$ for a non-negligible $\epsilon$, then $\mathsf {LinCExtract}$ outputs L in polynomial time with overwhelming probability.

In general we cannot efficiently check if the extracted $\boldsymbol{\beta }_j$ satisfies $\boldsymbol{\beta }_j \in S_f(\rho , \mathsf {com})$ since we cannot extract $\mathsf {op} _j$ corresponding to $(\boldsymbol{\beta }_j, \mathbf {z}_j)$, hence the term “almost” straight-line extractable. This implies that the set L may include an invalid $(\boldsymbol{\beta }_j, \mathbf {z}_j)$ for which there does not exist a valid $\mathsf {op} _j$. However, this will not be an issue for most of our application where f defines the entire verification algorithm of the underlying $\varSigma$-protocol. In these cases, we only need $f(\boldsymbol{\beta }_j, \mathbf {z}_j) = \top$ for k-tuples to hold to invoke the k-special soundness extractor. We also point out that in many cases we are not able to efficiently compute the cardinality of the set $S_f(\rho , \mathsf {com})$ so we do not know if $\mathsf {LinCExtract}$ runs in polynomial time. However, in typical applications, we can deduce that $S_f(\rho , \mathsf {com})$ must be of size $\left| \mathsf { ChSet} \right| \cdot \epsilon$ for a non-negligible $\epsilon$ unless the adversary breaks some other intractable problem.

Optional. Finally, we consider two optional properties for $\mathcal {F}$-almost straight-line extractability that help simplify the proofs in some cases. The first property is useful when the underlying public-coin $\mathsf{HVZK}$ interactive protocol already uses a small (i.e., $\mathsf {poly}$-large) challenge set. These shows up in multi-round protocols where the verifier may sample randomness from different challenge sets in each round. (See Sect. 5 for an example.) The second property allows to argue that for each challenge $\boldsymbol{\beta }\in \mathsf { ChSet}$, there exist at most one response $\mathbf {z}$ that passes the verification. Due to page limitation, we omit the details to the full version.

3.2 Simplified Definition of Extractable $\mathsf {LinHC}$

In case the goal is to construct quantum secure $\varSigma$-protocols (and not a QROM secure simulation extractable $\mathsf{NIZK}$ or a signature), we can use a simplified definition of extractable $\mathsf {LinHC}$ protocols in the standard model. One of the main simplification comes from the fact that since all of the security notions are decoupled from the QRO, the proofs follow much like the classical counterparts. For example, zero-knowledge of a simplified extractable $\mathsf {LinHC}$ protocol is defined similarly to standard $\mathsf{naHVZK}$ of a $\varSigma$-protocol. We omit the details to the full version.

3.3 Interlude: Extractable $\mathsf {LinHC}$ Specialized for Lattices

In most, if not all, lattice-based $\varSigma$-protocols, the witness being proven is a “short” vector. Therefore, throughout this work, we assume such shortness condition holds by default and integrate it into the definition of the extractable $\mathsf {LinHC}$ protocol. Effectively, we are able to construct a more efficient extractable $\mathsf {LinHC}$ protocol by taking advantage of these bounds.

  In the following, we assume the size of the vectors $( \mathbf {e}_i )_{i \in [N]}$ and $\mathbf {r}$ in $R_q^m$ have an upper bound. That is, for all $i \in [N]$, there exist positive integers $B_{\infty , \mathbf {e}}, B_{2, \mathbf {e}}, B_{\infty , \mathbf {r}}$, and $B_{2, \mathbf {r}}$ such that ${\Vert \mathbf {e}_i \Vert }_\infty \le B_{\infty , \mathbf {e}_i}$, ${\Vert \mathbf {e}_i \Vert }_2 \le B_{2, \mathbf {e}_i}$, ${\Vert \mathbf {r} \Vert }_\infty \le B_{\infty , \mathbf {r}}$ and ${\Vert \mathbf {r} \Vert }_2 \le B_{2, \mathbf {r}}$. In particular, we only guarantee correctness and $\mathsf{naHVZK}$ for such $\mathbf {e}_i$’s and $\mathbf {r}$.

  As explained in the previous section, the function class $\mathcal {F}$ of $\mathcal {F}$-almost straight-line extractability (Definition 3.4) corresponds to the the check performed by the verifier of the underlying $\varSigma$-protocol, which we are trying to make secure in the (Q)ROM via extractable $\mathsf {LinHC}$. Namely, the verifier of the $\varSigma$-protocol receives $\mathbf {z}$ from the prover and then checks whether some condition $f \in \mathcal {F}$ holds with respect to the challenge $\boldsymbol{\beta }$ it sampled, i.e., $f(\boldsymbol{\beta }, \mathbf {z}) {\mathop {=}\limits ^{\mathrm {?}}}\top$. In any lattice-based $\varSigma$-protocol, one of the conditions that is always checked by the verifier is whether $\mathbf {z}$ is “small” (see Sect. 4.1 for a concrete example). We therefore restrict the function class $\mathcal {F}$ to be a family of functions $\mathcal {F}_{B}$ such that for any $f \in \mathcal {F}_{B}$, f includes the check ${\Vert \mathbf {z} \Vert }_2 \le B$.¹⁵ In many lattice-based $\varSigma$-protocols, we have $B \approx B_{\infty , \mathbf {r}}$ or $B_{2, \mathbf {r}}$, where recall $\mathbf {r}$ is the “masking” term to hide $( \mathbf {e}_i )_{i \in [N]}$.

3.4 Construction of Extractable $\mathsf {LinHC}$

We propose two constructions of extractable $\mathsf {LinHC}$ protocols: one based only on $\mathsf {MLWE}$ and the other based on $\mathsf {MLWE}$ and $\mathsf {DSMR}$. Since the two constructions are almost identical, we explain the former and refer the details on the latter to the full version. The latter has proof size half of the former while relying on the extra $\mathsf {DSMR}$ assumption. The construction of our first extractable $\mathsf {LinHC}$ protocol based on $\mathsf {MLWE}$ is provided in Fig. 2.

Fig. 2.

An extractable $\mathsf {LinHC}$ protocol based on $\mathsf {MLWE}$.

Parameters and asymptotic size. Let the dimension d of the ring $R_q$ be larger than 256 and n, m be positive integers such that $n \le m$,¹⁶ $p < q$ be coprime odd integers, $\eta$ a positive real, and $\mathsf {H}$ be a random oracle with domain $\{ 0,1 \} ^\nu$ and range $R_q^{m \times n} \times R_q^{m \times n}$. The concrete value of $\nu$ is specific to the underlying $\varSigma$-protocol being used. Let $T, \phi$, and $\mathsf {err}$ be parameters required by the rejection sampling algorithm, where we set $T = \eta \cdot \sum ^N_{i = 1} {\Vert \beta _i \Vert }_\infty \cdot \sqrt{(n + 2m)d}$.

The size of the first message $\mathsf {com}$ is $2 md (N+1) \log q$ and the third message $\mathsf {op}$ is $(n + 2m) d\cdot \log (10 \phi T)$. Looking ahead, when we make the protocol non-interactive via the Fiat-Shamir transform, we can send the challenge $\boldsymbol{\beta }$ instead of $(\mathbf {w}_1, \mathbf {w}_2)$ since the latter can be recovered from the other components and $\boldsymbol{\beta }$. Then, the total size becomes $2mdN \log q+ (n + 2m)d \cdot \log (10 \phi T) + \left| \mathsf { ChSet} \right|$.

Properties. Due to page limitation, we omit the details of the proof of correctness and the quantum accessible non-abort $\mathsf{HVZK}$ ($\mathsf{QAnaHVZK}$) to the full version. We note that for $\mathsf{QAnaHVZK}$, we rely on the quantum accessible $\mathsf {MLWE}$ assumption.

Fig. 3.

Description of $\mathsf {SimOracle}$, $\widetilde{\mathsf {H}}$, and $\mathsf {LinCExtract}$ for the extractable $\mathsf {LinHC}$ protocol in Fig. 2. Here the PRF key $\mathsf {K}$ is assumed to be hardwired to $\widetilde{\mathsf {H}}$ and denote $L_{\boldsymbol{\beta }}$ as the set .

Lemma 3.1

( -Almost straight-line extractable). Assume $B \ge \sqrt{2nd} \cdot \phi \cdot T$, $2\sqrt{2}p ( nd\eta + \sqrt{nm} d\eta + \sqrt{nd}) \phi T + 2B < q/2$, and $B \le (p-1)/4$. Define the oracle simulator $\mathsf {SimOracle}$ and linear commitment extractor $\mathsf {LinCExtract}$ as in Fig. 3, where $T^*$ in Line 6 of algorithm $\mathsf {LinCExtract}$ is $T^*= \frac{k \cdot \delta \cdot \left| \mathsf { ChSet} \right| }{\left| S_f(\rho , \mathsf {com}) \right| - k}$. Then, the extractable $\mathsf {LinHC}$ protocol in Fig. 2 is $\mathcal {F}_{B}$-almost straight-line extractable. Moreover, for any QPT adversary $\mathcal {A}$ that distinguishes between a random $\mathsf {H}$ and $\widetilde{\mathsf {H}}$ output by $\mathsf {SimOracle}$ making at most Q queries, there exists a QPT adversary $\mathcal {B} _1$ against the quantum accessible $\mathsf {MLWE} _{m, n, 2^\nu , Q, \eta }$ problem and a QPT adversary $\mathcal {B} _2$ against the quantum accessible $\mathsf {PRF}$ such that

$$\begin{aligned} \mathsf {Adv}^{\mathsf {IndO}}(\mathcal {A}) \le m \cdot \mathsf {Adv}^{\mathsf {qaMLWE} _{m, n, 2^\nu , Q, \eta }}( \mathcal {B} _1 ) + \mathsf {Adv}^{\mathsf {qaPRF}}(\mathcal {B} _2), \end{aligned}$$

where $\mathsf {Time} (\mathcal {A}) = \mathsf {Time} (\mathcal {B} _1) \approx \mathsf {Time} (\mathcal {B} _2)$.

Proof

We only prove Item 2 below and refer the others to the full version.

Item 2. Fix any $(\widetilde{\mathsf {H}}, \tau = \mathsf {K})$, randomness $\rho \in \{ 0,1 \} ^\nu$, first message $\mathsf {com} = \big ( ( \mathbf {t}_{i,1}, \mathbf {t}_{i, 2} )_{i \in [N]}, \mathbf {w}_1, \mathbf {w}_2 \big )$, and any function $f \in \mathcal {F}_{B}$. Moreover, let $\mathsf {trans} = (\mathsf {com}, \boldsymbol{\beta }, (\mathbf {z}, \mathsf {op}))$ be a valid transcript. We first show that conditioned on 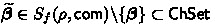being sampled in Line 7, $\mathsf {LinCExtract} ( \tau , \rho , \mathsf {trans})$ always succeeds in outputting a valid $\widetilde{\mathbf {z}}$ such that $f(\widetilde{\boldsymbol{\beta }}, \widetilde{\mathbf {z}}) = \top$. By definition of the set $S_f(\rho , \mathsf {com})$, existence of $(\widetilde{\mathbf {z}}, \widetilde{\mathsf {op}})$ such that $\mathsf{Verify} (\mathsf {K}_\mathsf{com}, (\mathsf {com}, \widetilde{\boldsymbol{\beta }}, (\widetilde{\mathbf {z}}, \widetilde{\mathsf {op}}))) = \top$ and $f(\widetilde{\boldsymbol{\beta }}, \widetilde{\mathbf {z}}) = \top$ is guaranteed. Therefore, denoting $\widetilde{\mathsf {op}} = [\widetilde{\mathbf {z}}_1 \Vert \widetilde{\mathbf {z}}_2 \Vert \widetilde{\mathbf {z}}_3]$, we have ${\Vert \widetilde{\mathbf {z}}_\ell \Vert }_2 \le \sqrt{2nd} \cdot \phi \cdot T$ for all , and $p \cdot (\mathbf {A}\widetilde{\mathbf {z}}_1 + \widetilde{\mathbf {z}}_2) = \sum ^N_{i = 1} \widetilde{\beta }_i \cdot \mathbf {t}_{i, 1} + \mathbf {w}_1, \quad p \cdot (\mathbf {B}\widetilde{\mathbf {z}}_1 + \widetilde{\mathbf {z}}_3) + \widetilde{\mathbf {z}}= \sum ^N_{i = 1} \widetilde{\beta }_i \cdot \mathbf {t}_{i, 2} + \mathbf {w}_2,$ where $\mathbf {A}$ and $\mathbf {B}= \mathbf {D}_1 \mathbf {A}+ \mathbf {D}_2$ are uniquely defined by $\widetilde{\mathsf {H}} (\rho )$ and $\tau = \mathsf {K}$ as in Fig. 3. Therefore, since $\mathbf {v}:= ( \sum ^N_{i = 1} \widetilde{\beta }_i \cdot \mathbf {t}_{i, 2} + \mathbf {w}_2 ) - \mathbf {D}_1 ( \sum ^N_{i = 1} \widetilde{\beta }_i \cdot \mathbf {t}_{i, 1} + \mathbf {w}_1 ) = p \cdot ( \mathbf {D}_2 \widetilde{\mathbf {z}}_1 - \mathbf {D}_1\widetilde{\mathbf {z}}_2 + \widetilde{\mathbf {z}}_3 ) + \widetilde{\mathbf {z}}$, we have

$$\begin{aligned} \Vert \mathbf {v}\Vert _\infty \le&p \cdot \big ( \sqrt{nd} {\Vert \mathbf {D}_2 \Vert }_\infty \cdot {\Vert \widetilde{\mathbf {z}}_1 \Vert }_2 + \sqrt{md} {\Vert \mathbf {D}_1 \Vert }_\infty \cdot {\Vert \widetilde{\mathbf {z}}_2 \Vert }_2 + {\Vert \widetilde{\mathbf {z}}_3 \Vert }_\infty \big ) + {\Vert \widetilde{\mathbf {z}} \Vert }_\infty \\ \le&\sqrt{2}p ( nd\eta + \sqrt{nm} d\eta + \sqrt{nd}) \phi T + 2B < q/2, \end{aligned}$$

where we have ${\Vert \widetilde{\mathbf {z}} \Vert }_2 \le B$ by definition of $\mathcal {F}_{B}$ (see Sect. 3.3), ${\Vert \mathbf {D}_1 \Vert }_\infty , {\Vert \mathbf {D}_2 \Vert }_\infty \le \eta$, and the last equation holds from the assumption in the statement. Moreover, we use the fact that for two vectors $\mathbf {a}, \mathbf {b}\in \mathbb {Z}^n$, we have ${\Vert \mathbf {a}^\top \mathbf {b} \Vert }_\infty \le \sqrt{n}{\Vert \mathbf {a} \Vert }_\infty {\Vert \mathbf {b} \Vert }_2$. This implies that the equality holds over R, and in particular, when ${\Vert \widetilde{\mathbf {z}} \Vert }_\infty \le B \le (p-1)/2$, $\big ( \sum ^N_{i = 1} \widetilde{\beta }_i \cdot \mathbf {t}_{i, 2} + \mathbf {w}_2 \big ) - \mathbf {D}_1 \big ( \sum ^N_{i = 1} \widetilde{\beta }_i \cdot \mathbf {t}_{i, 1} + \mathbf {w}_1 \big ) \mod p$ is identical to $\widetilde{\mathbf {z}}$. Hence, we are able to extract $\widetilde{\mathbf {z}}$ such that $f(\widetilde{\boldsymbol{\beta }}, \widetilde{\mathbf {z}}) = \top$.

Next, we check that $\mathsf {LinCExtract}$ succeeds in outputting a set such that $f(\widetilde{\boldsymbol{\beta }}_j, \widetilde{\mathbf {z}}_j) = \top$ for all $j \in [k]$, where by construction all the $\widetilde{\boldsymbol{\beta }}_j$’s are pairwise distinct. Since $\widetilde{\boldsymbol{\beta }}$ is sampled uniformly random from $\mathsf { ChSet} \backslash L_{\boldsymbol{\beta }}$, the probability of sampling $\widetilde{\boldsymbol{\beta }}\in S_f(\rho , \mathsf {com}) \backslash L_{\boldsymbol{\beta }}$ in one loop is at least $\frac{ \left| S_f(\rho , \mathsf {com}) \right| - k }{ \left| \mathsf { ChSet} \right| }$. Therefore, given any L, if we sample $\widetilde{\boldsymbol{\beta }}$ $\frac{ \delta \cdot \left| \mathsf { ChSet} \right| }{ \left| S_f(\rho , \mathsf {com}) \right| - k }$-times from the set $\mathsf { ChSet} \backslash L_{\boldsymbol{\beta }}$, then the probability of sampling $\widetilde{\boldsymbol{\beta }}\in S_f(\rho , \mathsf {com}) \backslash L_{\boldsymbol{\beta }}$ is at least $1 - 2^{-\delta }$. Since each loop is independent from each other, after $T^* = \frac{k \cdot \delta \cdot \left| \mathsf { ChSet} \right| }{\left| S_f(\rho , \mathsf {com}) \right| - k}$-loops, we obtain the desired set L with probability at least $1 - k \cdot 2^{-\delta }$, where the bound follows from the union bound. Finally, since each loop takes a fixed polynomial time, the running time of $\mathsf {LinCExtract}$ is $T^*\cdot \mathsf {poly}(\kappa )$ as desired. We note that there could exist $\widetilde{\boldsymbol{\beta }}\not \in S_f(\rho , \mathsf {com})$ for which $\mathsf {LinCExtract}$ succeeds in extracting $\widetilde{\mathbf {z}}$ such that $f(\widetilde{\boldsymbol{\beta }}, \widetilde{\mathbf {z}}) = \top$. However, this will not be a problem since such $\widetilde{\boldsymbol{\beta }}$ can only increase the success probability and lower the running time of $\mathsf {LinCExtract}$.

This completes the proof of Item 2.    $\square$

We note that we can get an asymptotically more efficient extractor by allowing algorithm $\mathsf {LinCExtract}$ to be QPT and perform Grover’s search. Finally, we also discuss how to “downgrade” the above extractable $\mathsf {LinHC}$ protocol to only satisfy the properties of a simplified/classical extractable $\mathsf {LinHC}$ protocol. The benefit of doing this is that it provides tighter reductions since we no longer need to work with QROs. The details are provide in the full version.

4 How to Use Extractable $\mathsf {LinHC}$

In this section, we provide a basic example of bootstrapping the ROM secure Lyubashevsky’s $\varSigma$-protocol [27, 28] to be QROM secure using an extractable $\mathsf {LinHC}$ protocol. The aim of this section is to provide a guide on how to prove QROM security using an extractable $\mathsf {LinHC}$ protocol. In Sect. 5, we see how these ideas can be used to prove QROM security of more complex protocols.

As explained in the beginning of Sect. 3, we can either construct a (1) quantum straight-line extractable $\varSigma$-protocol using the simplified extractable $\mathsf {LinHC}$ protocol (see Sect. 3.2) or a (2) quantum secure simulation straight-line extractable $\mathsf{NIZK}$ (or a signature scheme) using the standard extractable $\mathsf {LinHC}$ protocol. We explain both items. The former is easier to prove and makes it simpler to understand the essence of the extractable $\mathsf {LinHC}$ protocol, while the latter provides a stronger and more useful result.

4.1 Lyubashevsky’s $\varSigma$-Protocol $\Rightarrow$ Quantum Secure $\varSigma$-Protocol via Simplified Extractable $\mathsf {LinHC}$

We show how to make the classical lattice-based $\varSigma$-protocol of Lyubashevsky into a $\varSigma$-protocol that is quantum straight-line proof of knowledge in the CRS model by integrating it with a simplified extractable $\mathsf {LinHC}$ in the standard model. Below, we denote Lyubashevsky’s $\varSigma$-protocol as $\varSigma _\mathsf {Lyu}$-protocol.

Preparation. Let $\mathsf { ChSet} \subset \{ 0,1 \} ^\kappa$ be a set such that all $\beta \in \mathsf { ChSet}$ satisfies $\Vert \beta \Vert _1 \le \ell$. Here, $\ell$ is chosen in such a way to guarantee ${n \atopwithdelims ()\ell } \ge 2^{256}$. Let $\phi$ and $\mathsf {err}$ be parameters specified by the rejection sampling algorithm. Let $B_\mathbf {e}$, $B_\mathbf {r}$, and $B_\mathbf {z}$ be positive reals such that $B_\mathbf {r}\ge \sqrt{2md} \cdot \ell \cdot B_\mathbf {e}$ and $B_\mathbf {z}\ge \sqrt{2nd} \cdot \phi \cdot B_\mathbf {r}$. Define the $\mathsf {MSIS}$ relation as , where $\mathbf {A}\in R_q^{n \times m}$, $\mathbf {u}\in R_q^n$, and $\mathbf {e}\in R_q^m$. We also define the “relaxed” relation $\mathcal {R}'_\mathsf {MSIS}$ where the only difference between $\mathcal {R}_\mathsf {MSIS}$ is that $\mathbf {e}$ now only satisfies $\mathbf {A}\mathbf {e}= (\beta - \widetilde{\beta }) \cdot \mathbf {u}$ for some $\beta , \widetilde{\beta }\in \mathsf { ChSet}$ and ${\Vert \mathbf {e} \Vert }_2 \le B'_\mathbf {e}$ for a slightly larger bound $B'_\mathbf {e}> B_\mathbf {e}$. It is known that the $\varSigma _\mathsf {Lyu}$-protocol is $\mathsf{naHVZK}$ and satisfies relaxed 2-special soundness.

Quantum secure $\varSigma$-protocol. The construction is depicted in Fig. 4. $\mathsf{Setup}$ of the $\varSigma$ protocol runs $\mathsf {KeyGen}$ of the extractable $\mathsf {LinHC}$ protocol. Below, we show correctness, $\mathsf{naHVZK}$, and $\mathsf {SL\text {-}PoK}$ of our $\varSigma$-protocol in Fig. 4. Since the first two properties follows almost immediately from the underlying $\varSigma _\mathsf {Lyu}$-protocol and the simplified extractable $\mathsf {LinHC}$ protocol, we omit them to the full version.

Fig. 4.

Quantum secure $\varSigma$-protocol in the CRS model for the lattice relation $\mathbf {A}\mathbf {e}= \mathbf {u}$, where $\mathsf {crs}$ is $\mathsf {K}_\mathsf{com} \leftarrow \mathsf {KeyGen} (1^\kappa )$. The witness $\mathbf {e}$ satisfies ${\Vert \mathbf {e} \Vert }_2 \le B_\mathbf {e}$. The gray indicates the components that are used in the $\varSigma _\mathsf {Lyu}$-protocol.

Fig. 5.

Description of $\mathsf {SimSetup}$ and $\mathsf {SL\text {-}Extract}$ for the $\varSigma$-protocol in Fig. 4.

Lemma 4.1

($\mathsf {SL\text {-}PoK}$). Let the $\varSigma _\mathsf {Lyu}$-protocol for the relations $(\mathcal {R}_\mathsf {MSIS}, \mathcal {R}'_\mathsf {MSIS})$ be relax 2-special sound with extractor $\mathsf {Extract}_\mathsf{ss}$. Let the simplified extractable $\mathsf {LinHC}$ protocol be $\epsilon _\mathsf {IndCom}$-$\mathcal {F}_{B_\mathbf {z}}$-almost straight-line extractable with simulator ${\mathsf {SimKeyGen}}$ and linear commitment extractor $\mathsf {LinCExtract}$, where $\mathcal {F}_{B_\mathbf {z}}$ is the family of functions of the form $f_{\mathbf {A}, \mathbf {u}, \mathbf {w}}(\beta , \mathbf {z}) = \top$ if and only if ${\Vert \mathbf {z} \Vert }_2 \le B_\mathbf {z}$ and $\mathbf {A}\mathbf {z}= \beta \cdot \mathbf {u}+ \mathbf {w}$. Finally, let $T^* = ((\epsilon - \nu _2)/2-1/ \left| \mathsf { ChSet} \right| )^{-1}$ where $\epsilon$ is the advantage of the adversary $\mathcal {A}$ and $\nu _2$ is a negligible function as in the statement of Definition 2.1, and $\mathsf {poly}(\kappa )$ is some fixed polynomial independent of $\mathcal {A}$.

Then our $\varSigma$-protocol in the CRS model for the relations $(\mathcal {R}_\mathsf {MSIS}, \mathcal {R}'_\mathsf {MSIS})$ in Fig. 4 is a straight-line $\mathsf {PoK}$ with simulator $\mathsf {SimSetup}$ and straight-line extractor $\mathsf {SL\text {-}Extract}$ described in Fig. 5.

Proof

Fix any $\mathsf {X} = (\mathbf {A}, \mathbf {u})$. Let $\mathcal {A}$ be a QPT algorithm that outputs a valid transcript with probability $\epsilon$ as in the statement of Definition 2.1. Then, we have

(1)

where $\alpha = (\mathbf {w}, \mathsf {com})$ and $\gamma = (\mathbf {z}, \mathsf {op})$. Let $\varGamma = \left| \mathsf { ChSet} \right| \cdot \frac{\epsilon - \epsilon _\mathsf {IndCom}}{2}$ which we assume to be a positive integer larger than 2 without loss of generality. Omitting the randomness for better readability, we can rewrite the l.h.s of Eq. (1) as

(2)

Here, $f \in \mathcal {F}_{B_\mathbf {z}}$ is the function that on input $(\beta , \mathbf {z})$, outputs $\top$ if and only if ${\Vert \mathbf {z} \Vert }_2 \le B_\mathbf {z}$ and $\mathbf {A}\mathbf {z}= \beta \cdot \mathbf {u}+ \mathbf {w}$, where $\mathbf {w}$ is the vector included in $\alpha$ output by $\mathcal {A}$. Since $\beta$ is sampled uniformly random from $\mathsf { ChSet}$ and independently of $\mathsf {com}$ output by $\mathcal {A}$, and $S_f( \widetilde{\mathsf {K}}_\mathsf{com}, \mathsf {com})$ is the set of $\beta$’s that permit a valid $(\mathbf {z}, \mathsf {op})$ we have $\Pr [ \mathsf{Verify} (\widetilde{\mathsf {crs}}, \mathsf {X}, (\alpha , \beta , \gamma ) ) = \top ~\wedge ~ |S_f( \widetilde{\mathsf {K}}_\mathsf{com}, \mathsf {com})|< \varGamma ] < \frac{\varGamma }{\left| \mathsf { ChSet} \right| } = \frac{\epsilon - \epsilon _\mathsf {IndCom}}{2}.$ Combining this with Eq. (1) and (2), we have $\Pr [ \mathsf{Verify} ( \widetilde{\mathsf {crs}}, \mathsf {X}, (\alpha , \beta , \gamma ) ) = \top ~\wedge ~ |S_f(\widetilde{\mathsf {K}}_\mathsf{com}, \mathsf {com})| \ge \varGamma ] \ge \frac{\epsilon - \epsilon _\mathsf {IndCom}}{2}.$ Specifically, with probability at least $\frac{\epsilon - \epsilon _\mathsf {IndCom}}{2}$, we have $|S_f(\widetilde{\mathsf {K}}_\mathsf{com}, \mathsf {com})| \ge \varGamma$. Conditioning on such an event, we have that $\mathsf {LinCExtract} ( \tau , (\mathsf {com}, \beta , (\mathbf {z}, \mathsf {op})) )$ outputs a tuple such that $\beta \ne \widetilde{\beta }$ and $f(\widetilde{\beta }, \widetilde{\mathbf {z}}) = \top$ in time at most $\left( \frac{\left| \mathsf { ChSet} \right| }{ \varGamma - 1 } \right) \cdot \mathsf {poly}_\mathsf {LinHC} (\kappa )$ with probability at least $1 - 2^{-\kappa }$, where we set $\delta = \kappa$. By setting $T^* = \frac{\left| \mathsf { ChSet} \right| }{ \varGamma - 1 }$ and $\mathsf {poly}(\kappa ) = \mathsf {poly}_\mathsf {LinHC} (\kappa )$ in Fig. 5, with probability at least $\frac{\epsilon - \epsilon _\mathsf {IndCom}}{2} \cdot (1 - 2^{-\kappa })$, $\mathsf {SL\text {-}Extract}$ moves on to Line 3. By definition of $f \in \mathcal {F}_{B_\mathbf {z}}$, $(\mathbf {w}, \beta , \mathbf {z})$ and $(\mathbf {w}, \widetilde{\beta }, \widetilde{\mathbf {z}})$ are two valid transcripts for the underlying classical $\varSigma$-protocol. Hence, we obtain $\mathbf {z}^* \leftarrow \mathsf {Extract}_\mathsf{ss} ( \mathbf {w}, (\beta , \mathbf {z}), (\widetilde{\beta }, \widetilde{\mathbf {z}}) )$ such that $(\mathsf {X}, \mathsf {W} = \mathbf {z}^*) \in \mathcal {R}'_\mathsf {MSIS}$ as desired. This completes the proof.    $\square$

4.2 Lyubashevsky’s $\varSigma$-Protocol $\Rightarrow$ QROM Secure Signature via Extractable $\mathsf {LinHC}$ and Fiat-Shamir

We show how to directly compile the $\varSigma _\mathsf {Lyu}$-protocol into an $\mathsf {eu\text {-}cma}$ secure signature scheme using the Fiat-Shamir transform The main technicality of this section is to show that even if an adversary gets to observe polynomially many simulated proofs (i.e., signatures), we are still able to extract a witness from a valid proof (i.e., extract the secret key from a signature forgery) output by the adversary without rewinding.

QROM secure signature scheme. The construction of our (deterministic) signature scheme in the QROM is provided in Fig. 6.¹⁷ The algorithms are provided oracle access to the random oracle $\mathsf {H}$, and we use appropriate domain separation to simulate two independent random oracles with different domains and ranges: $\mathsf {H} _{\mathtt {LHC}}$ for the extractable $\mathsf {LinHC}$ protocol and $\mathsf {H} _{\mathtt {FS}}$ for applying the Fiat-Shamir transform The output space of $\mathsf {H} _{\mathtt {FS}}$ is . Let all the parameters be defined identically to those of the $\varSigma$-protocol. We assume that each first message ($\mathbf {w}= \mathbf {A}\mathbf {r}$) of the underlying $\varSigma _\mathsf {Lyu}$-protocol has $\zeta$-min-entropy and further assume with overwhelming probability that there exists at least two short vectors $\mathbf {e}, \mathbf {e}' \in S^m_{B_\mathbf {e}}$ such that $\mathbf {A}\mathbf {e}= \mathbf {A}\mathbf {e}' = \mathbf {u}$. Both of these assumptions are standard in prior works.

Fig. 6.

QROM secure signature scheme by applying the Fiat-Shamir transform to our $\varSigma$-protocol in Fig. 4. Oracles $\mathsf {H} _{\mathtt {LHC}}$ and $\mathsf {H} _{\mathtt {FS}}$ are implemented using $\mathsf {H}$.

Properties. Due to page limitation, we provide the proof of $\mathsf {eu\text {-}cma}$ security in the full version. For an overview of the proof, we refer the readers to the technical overview in Sect. 1.2. The main technicality of the proof is showing that with high probability, there must have been another challenge the adversary was able to forge on even though it had some control over which challenge it used through quantumly accessing the random oracle $\mathsf {H} _{\mathtt {FS}}$.

5 Application: Quantum Secure 5-Round Public-Coin Exact Sound Proof and $\mathsf{NIZK}$

In this section, to showcase the generality of the extractable $\mathsf {LinHC}$ protocol, we show how to integrate it to the recent 5-round public-coin $\mathsf{HVZK}$ interactive exact sound proof of Bootle et al. [8]. The main motivation for choosing [8] as the case study is because the ideas presented in this section can be directly applied to other recent works [1, 3, 15, 35]. We can convert the protocol of [8] into either (1) a quantum secure straight-line extractable interactive proof using the simplified extractable $\mathsf {LinHC}$ protocol (as in Sect. 4.1) or (2) into a quantum secure simulation straight-line extractable $\mathsf{NIZK}$ (or a signature scheme) using the extractable $\mathsf {LinHC}$ protocol (as in Sect. 4.2).

5.1 Quantum Secure Exact Sound Interactive Proof via Simplified Extractable $\mathsf {LinHC}$

We first show how to apply the simplified extractable $\mathsf {LinHC}$ protocol to Bootle et al.’s protocol [8] to obtain a 5-round public-coin interactive proof that is quantum secure, straight-line extractable, and exact sound. In brief, Bootle et al. constructs an interactive protocol that allows the prover to prove knowledge of a vector satisfying $\mathbf {A}\mathbf {s}= \mathbf {u}$, where the main difference between Lyubashevsky’s protocol is that it exact sound. That is, a knowledge extractor extracts a witness that satisfies the original relation used by the prover (and not a “relaxed” relation). While zero-knowledge of our protocol is a direct consequence of that of Bootle et al.’s protocol, soundness needs slightly more work.

Parameters. Following Bootle et al., we chose the dimension d and modulus q so that $R_q$ completely splits into d linear factors modulo q, e.g., d is a power of 2 and $q \equiv 1 \mod 2d$. For a ring element $s \in R_q$, we denote $\hat{\mathbf {s}}\in \mathbb {Z}^d_q$ as the NTT representation of s. Then, for a matrix-vector pair $(\mathbf {A}, \mathbf {u}) \in \mathbb {Z}_q^{m \times d} \times \mathbb {Z}_q^m$, we consider the relation . Let $C$ denote the set , and $\phi$ and $\mathsf {err}$ be parameters specified by the rejection sampling algorithm. Let $B_\mathbf {e}$, $B_\mathbf {r}$, and $B_\mathbf {z}$ be positive reals such that $B_\mathbf {r}\ge \sqrt{6d} \cdot B_\mathbf {e}$ and $B_\mathbf {z}\ge \sqrt{12d} \cdot \phi \cdot B_\mathbf {r}$, where the size of $B_\mathbf {e}$ dictates the hardness of the $\mathsf {MLWE}$ assumption.

Quantum secure exact sound protocol. The protocol is depicted in Fig. 7. It can be seen that the way we apply the extractable $\mathsf {LinHC}$ protocol is very similar to what was done for Lyubashevsky’s protocol (see Fig. 4). Correctness and $\mathsf{naHVZK}$ are straightforward to prove and we omit them to the full version.

Fig. 7.

Quantum secure exact sound public-coin interactive protocol in the CRS model for the relation $\mathcal {R}_\mathsf {ES}$. $\mathbf {B}\in R_q^{5 \times 6}$ is the public parameter of the (implicit) commitment scheme $\varPi _\mathsf{Com}$ $\varPi _\mathsf{Com}$, and $\mathbf {b}^\top _i$ denotes its i-th row vector. The gray indicates the components that are used in the protocol of Bootle et al. [8].

The high level idea of the proof for straight-line proof of knowledge is similar to those provided by Bootle et al. [8, Theorem 3.1]. The main difference is how we extract a witness from partial valid transcripts. Recall Bootle et al. first rewinds the adversary to obtain six valid transcripts with a specific form and then shows how to extract a witness from such transcripts. In our proof, we are only able to extract a small portion of the six valid transcripts so we need to rely on a different argument compared to Bootle et al.

Lemma 5.1

($\mathsf {SL\text {-}PoK}$). Let the simplified extractable $\mathsf {LinHC}$ protocol be $\epsilon _\mathsf {IndCom}$-$\mathcal {F}_{B_\mathbf {z}}$-almost straight-line extractable with simulator ${\mathsf {SimKeyGen}}$ and linear commitment extractor $\mathsf {LinCExtract}$, where $\mathcal {F}_{B_\mathbf {z}}$ is the singleton set for a f such that $f(\beta , \mathbf {z}) = \top$ if and only if ${\Vert \mathbf {z} \Vert }_2 \le B_\mathbf {z}$.

Then, there exists a PPT simulator $\mathsf {SimSetup}$ and a straight-line extractor $\mathsf {SL\text {-}Extract}$ with the following property: Let $\mathcal {A}$ be an adversary that outputs a valid transcript with probability $\epsilon > 3/q + 2/d$¹⁸ Then, on input a valid transcript output by $\mathcal {A}$ executed on a simulated $\mathsf {crs}$ output by $\mathsf {SimSetup}$, $\mathsf {SL\text {-}Extract}$ outputs either a witness $s \in R_q$ in the relation $\mathcal {R}_\mathsf {ES}$ or a $\mathsf {MSIS} _{n, 6n, 8B_\mathbf {z}}$ solution for $\mathbf {b}^\top _1$ with probability $(\epsilon - \nu )/3$ for a negligible function $\nu$. Moreover, the runtime of $\mathsf {SL\text {-}Extract}$ is independent of the runtime of $\mathcal {A}$ and depends only polynomially on d and $\log q$.

Proof

Assume $\mathcal {A}$ successfully fools the honest verifier with advantage $\epsilon > 3/q + 2/d$ and the resulting transcript is $\mathsf {trans} ^* = \big ( (\mathbf {t}, \mathbf {w}, \mathsf {com}), c^{(1)}, (z_0^{(1)}, x_0^{(1)}, x^{(1)}_1, x^{(1)}_2), \beta ^{(1, 1)}, (\mathbf {z}^{(1, 1)}, \mathsf {op} ^{(1, 1)}) \big )$. Firstly, since $\mathcal {A}$ has advantage greater than $3/q + 2/d$, using the same statistical argument made in the proof of Lemma 4.1, with probability at least 1/3, the transcript $\mathsf {trans} ^*$ output by $\mathcal {A}$ satisfies the following property: there exists at least three distinct first challenges $c^{(1)}, c^{(2)}, c^{(3)} \in \mathbb {Z}_q$ and two distinct second challenges $\beta ^{(k, 1)}, \beta ^{(k, 2)} \in C$ for each $k \in [3]$ such that there exists some third message $( z_0^{(k)}, x_0^{(k)}, x^{(k)}_1, x^{(k)}_2 )$ and fifth message $(\mathbf {z}^{(k, j)}, \mathsf {op} ^{(k, j)})$ where $\mathsf {trans} ^{(k, j)} = \big ( (\mathbf {t}, \mathbf {w}, \mathsf {com}), c^{(k)}, (z_0^{(k)}, x_0^{(k)}, x^{(k)}_1, x^{(k)}_2), \beta ^{(k, j)}, (\mathbf {z}^{(k, j)}, \mathsf {op} ^{(k, j)}) \big )$ is a valid transcript for all $(k, j) \in [3] \times [2]$. Below, we first show how $\mathsf {SL\text {-}Extract}$ obtains a list that contains all $( ( \beta ^{(k, j)}, \mathbf {z}^{(k, j)} ) )_{(k, j) \in [3] \times [2]}$ using the straight-line extractability of the simplified extractable $\mathsf {LinHC}$ protocol.

We define $\mathsf {SimSetup}$ to run $(\widetilde{\mathsf {K}}_\mathsf{com}, \tau ) \leftarrow {\mathsf {SimKeyGen}} (1^\kappa )$ and output $\mathsf {crs} = (\mathbf {B}, \widetilde{\mathsf {K}}_\mathsf{com})$. Due to the simplified $\epsilon _\mathsf {IndCom}$-$\mathcal {F}_{B_\mathbf {z}}$-almost straight-line extractability, $\mathcal {A}$ still has advantage $(\epsilon - \epsilon _\mathsf {IndCom})/3$ in outputting a valid transcript $\mathsf {trans} ^*$ with the above property run on this modified $\mathsf {crs}$. Next, $\mathsf {SL\text {-}Extract}$ can use the extractor of the simplified extractable $\mathsf {LinHC}$ protocol $\mathsf {LinCExtract} (\tau , \mathsf {trans} ^*)$ to obtain a set $L = ( ( \beta _j, \mathbf {z}_j ) )_{j \in [ d ]}$ in time polynomial in $\left| C \right| = d$¹⁹, where we are guaranteed to extract all $\beta \in C$ that has a corresponding $(\mathbf {z}',\mathsf {op} ')$ such that $\mathsf{Verify} ( \mathsf {K}_\mathsf{com}, (\mathsf {com}, \beta , (\mathbf {z}', \mathsf {op} ')) ) = \top$ and ${\Vert \mathbf {z}' \Vert }_2 \le B_\mathbf {z}$. That is, all the extracted $\beta$ satisfies $\beta \in S_f(\mathsf {K}_\mathsf{com}, \mathsf {com})$. Moreover, once $\mathsf {com}$ is fixed, there exists at most one $\mathbf {z}'$ satisfying $\mathsf{Verify} ( \mathsf {K}_\mathsf{com}, (\mathsf {com}, \beta , (\mathbf {z}', \mathsf {op} ')) ) = \top$ for each $\beta \in C$ and any $\mathsf {op} '$ regardless of the choice of the second and third messages (i.e., $c \in \mathbb {Z}_q$ and $(z, w, x_1, x_2)$).²⁰ Therefore, the extracted $\mathbf {z}$ must be the unique $\mathbf {z}'$. Combining the argument so far, we have established $( (\beta ^{(k, j)}, \mathbf {z}^{(k, j)}) )_{(k, j) \in [3] \times [2]} \subseteq L$. Here, note $\beta ^{(k, j)}$ and $\beta ^{(k', j')}$ may be the same when $k \ne k'$. In the following, we show how $\mathsf {SL\text {-}Extract}$ determines which two tuples $(\beta , \mathbf {z})$ and $(\beta ', \mathbf {z}') \in L$ correspond to the tuples $(\beta ^{(k, 1)}, \mathbf {z}^{(k, 1)})$ and $(\beta ^{(k, 2)}, \mathbf {z}^{(k, 2)})$.

Assume we knew which elements in the set L corresponded to $(\beta ^{(k,1)}, \mathbf {z}^{(k, 1)})$ and $(\beta ^{(k, 2)}, \mathbf {z}^{(k, 2)})$ for each $k \in [3]$. Then, since $( \mathsf {trans} ^{(k, j)} )_{(k, j) \in [3] \times [2]}$ are valid transcripts, we have $\mathbf {b}_1^\top \mathbf {z}^{(k)} = \beta ^{(k, j)} \cdot t_1 + x_0^{(k)}$ for an unknown $x_0^{(k)}$. By subtracting $j = 1, 2$ for each $k \in [3]$, we can remove $x_0^{(k)}$ to obtain $\mathbf {b}_1^\top \mathbf {z}^{(k)} - \beta ^{(k, 1)} \cdot t_1 = \mathbf {b}_1^\top \mathbf {z}^{(k)} - \beta ^{(k, 2)} \cdot t_1$. Notice that we can check this equality with only knowledge of $\mathbf {B}$ in the $\mathsf {crs}$ and $\mathbf {t}$ in the first message, which is shared among all the transcripts. With this observation in mind, $\mathsf {SL\text {-}Extract}$ performs the following:

• 1. Prepare an empty list S and counter $t = 1$.

• 2. For each pair $(\beta , \mathbf {z}), (\beta ', \mathbf {z}') \in L$, check if $\mathbf {b}_1^\top \mathbf {z}- \beta \cdot t_1 = \mathbf {b}_1^\top \mathbf {z}' - \beta ' \cdot t_1$. If not move on to the next pair. Otherwise, add $(t, (\beta . \mathbf {z}), (\beta ', \mathbf {z}') )$ to the list S, update $t = t + 1$, and move on to the next pair.

For each $(t, (\beta , \mathbf {z}), (\beta ', \mathbf {z}') ) \in S$, denote ${\overline{\beta }}_t = \beta - \beta '$ and ${\overline{\mathbf {z}}}_t = \mathbf {z}-\mathbf {z}'$. Then, we have $\mathbf {b}^\top _1 {\overline{\mathbf {z}}}_t = {\overline{\beta }}_t \cdot t_1$, which is an approximate solution to the first equation of the commitment $\mathbf {t}$. Therefore, we can compute openings $\mathsf {M}_{t, 2}$, $\mathsf {M}_{t, 3}$ and $\mathsf {M}_{t, 4}$ and $\mathsf {M}_{t, 5}$ of $\mathbf {t}$ by setting $\mathsf {M}_{t, \ell } = t_\ell - {\overline{\beta }}^{-1}_t \cdot (\mathbf {b}^\top _\ell {\overline{\mathbf {z}}}_t) \in R_q$ for each . Here, note that these openings are valid relaxed openings for the commitment scheme with ${\Vert {\overline{\mathbf {z}}}_t \Vert }_2 \le 2 B_\mathbf {z}$. Hence, unless $\mathcal {A}$ breaks the binding property of the commitment, we are guaranteed that $\mathsf {M}_{t, 2}$, $\mathsf {M}_{t, 3}$, $\mathsf {M}_{t, 4}$, and $\mathsf {M}_{t, 5}$ are the same value for all $t \in \left| S \right|$. Conditioning on $\mathcal {A}$ not breaking the $\mathsf {MSIS} _{n, 6n, 8B_\mathbf {z}}$ problem, $\mathsf {SL\text {-}Extract}$ outputs $s^* := \mathsf {M}_{1, 3} = \cdots = \mathsf {M}_{\left| S \right| , 3}$ as the witness. Here, observe that the runtime of $\mathsf {SL\text {-}Extract}$ is only polynomially related to $\left| C \right| = d$: it takes time $d \cdot \mathsf {poly}(\kappa )$ to prepare the list L and takes time at most $d^2 \cdot \mathsf {poly}(\kappa )$ to prepare the list S. Therefore, it remains to show that $s^* \in R_q$ output by $\mathsf {SL\text {-}Extract}$ indeed satisfies $\mathbf {A}\hat{\mathbf {s}}^* = \mathbf {u}$ and , where $\hat{\mathbf {s}}^* \in \mathbb {Z}^d_q$ is the NTT representation of $s^*$. In the following, since all the messages are the same unless $\mathcal {A}$ breaks the $\mathsf {MSIS} _{n, 6n, 8 B_\mathbf {z}}$ problem, we drop the subscript t from the messages $\mathsf {M}$ and further denote $y^* = \mathsf {M}_2$.

Although we do not know $( c^{(k)}, (z_0^{(k)}, x_0^{(k)}, x^{(k)}_1, x^{(k)}_2) )_{k \in [3]}$, we have L that is guaranteed to contain $(\beta ^{(k, j)}, \mathbf {z}^{(k, j)})_{(k, j) \in [3] \times [2]}$ included in $( \mathsf {trans} ^{(k, j)} )_{(k, j) \in [3] \times [2]}$. For each $(k, j) \in [3] \times [2]$ consider the following verification equation

$$ (\mathbf {b}_2^\top + c^{(k)} \cdot \mathbf {b}^\top _3) \mathbf {z}^{(k, j)} + \beta ^{(k, j)} \cdot z_0^{(k)}= \beta ^{(k, j)} \cdot (c^{(k)} \cdot t_3 + t_2) + x^{(k)}_1, $$

where recall that $z_0^{(k)}$ and $x^{(k)}_1$ are unknown but guaranteed to exist. Subtracting the equations for the same k and $j = 1, 2$, we obtain $(\mathbf {b}_2^\top + c^{(k)} \cdot \mathbf {b}^\top _3) {\overline{\mathbf {z}}}^{(k)} + {\overline{\beta }}^{(k)} \cdot z_0^{(k)} = {\overline{\beta }}^{(k)} \cdot (c^{(k)} \cdot t_3 + t_2),$ where ${\overline{\beta }}^{(k)} = \beta ^{(k, 1)} - \beta ^{(k, 2)}$ and ${\overline{\mathbf {z}}}^{(k)} = \mathbf {z}^{(k, 1)} - \mathbf {z}^{(k, 2)}$. Further substituting the commitment openings for $t_2$ and $t_3$ to the above equation and making routine calculation shows $z_0^{(k)} = y^* + c^{(k)} \cdot s^*$. By performing the same argument on the final verification equation and substituting the commitment openings for $t_4$ and $t_5$, we obtain

$$ ( (y^*)^2 s^*- y^* \mathsf {M}_4 + \mathsf {M}_5 ) + ( (y^* (2s^* - 3) - \mathsf {M}_4) s^* ) \cdot c^{(k)} + ( s^*(s^* - 1)(s^* - 2) ) \cdot (c^{(k)})^2 = 0. $$

Since this equation holds for all $k \in [3]$ and $c^{(1)} \ne c^{(2)} \ne c^{(3)} \in \mathbb {Z}_q$, we must have $s^*(s^* - 1)(s^* - 2) = 0$ over $R_q$. Applying the NTT transform, this equation implies that . Finally, by subtracting the second verification equation from one another, we get $\mathbf {A}(\hat{\mathbf {z}}_0^{(1)} - \hat{\mathbf {z}}_0^{(2)}) = (c^{(1)} - c^{(2)}) \cdot \mathbf {u}$. Since $c^{(1)} \ne c^{(2)}$ and we established $z_0^{(k)} = y^* + c^{(k)} \cdot s^*$ for each $k \in [3]$, this implies $\mathbf {A}\hat{\mathbf {s}}^* = \mathbf {u}$ as desired.

To summarize, with probability 1/3, L contains $( (\beta ^{(k, j)}, \mathbf {z}^{(k, j)}) )_{(k, j) \in [3] \times [2]}$. Conditioned on this fact, $\mathsf {SL\text {-}Extract}$ outputs a valid witness $s^* \in \mathcal {R}_\mathsf {ES}$ unless it finds a solution to the $\mathsf {MSIS} _{n, 6n, 8 B_\mathbf {z}}$ problem. Note that $\mathsf {SL\text {-}Extract}$ performs all the steps without explicitly knowing $( c^{(k)}, (z_0^{(k)}, x_0^{(k)}, x^{(k)}_1, x^{(k)}_2) )_{k \in [3]}$.    $\square$

5.2 QROM Secure Exact Sound $\mathsf{NIZK}$ via Extractable $\mathsf {LinHC}$ and Fiat-Shamir

Bootle et al. [8] transformed their interactive protocol into a classical $\mathsf{NIZK}$ in the ROM using the Fiat-Shamir transform. Noticing that the two challenge sets $\mathbb {Z}_q$ and C have different size, they provided a more optimized soundness amplification technique. We explain in detail how we can incorporate such optimization technique when we instantiate the extractable $\mathsf {LinHC}$ protocol with the two constructions provided in Sect. 3.4. Since most of the argument is identical to those of the previous section, we refer the details to the full version.

5.3 Comparison

We compare Bootle et al.’s ROM secure $\mathsf{NIZK}$ and our QROM secure $\mathsf{NIZK}$. We consider the application of proving knowledge of the ternary secret in $\mathsf {LWE}$ samples over $\mathbb {Z}_q$, which is commonly used in the literature to provide a basic benchmark, e.g., [5, 8]. Such relation captures the setting of FHE schemes and group signatures. Aiming at the 128-bit quantum security level, our provably quantum secure $\mathsf{NIZK}$ has a proof size of 2071 KB while Bootle et al.’s (heuristically quantum secure) $\mathsf{NIZK}$ has proof size of 812 KB.²¹ The overhead is around a factor of 2.6. The full detail on how we arrive at these values is provided in the full version. In contrast, if assume we were able to make Bootle et al.’s $\mathsf{NIZK}$ secure in the QROM using the extended Unruh transform [11] (see Footnote 4), the proof size becomes 44.9 MB, where the overhead is a larger factor of 51.8. For completeness, we provide the details in the full version. Finally, note that it is unclear whether the Fiat-Shamir transform in the QROM can be securely applied to Bootle et al.’s $\mathsf{NIZK}$.

5.4 Further Applications of Extractable $\mathsf {LinHC}$

We show that other recent $\varSigma$-/public-coin $\mathsf{HVZK}$ interactive protocols are compatible with our extractable $\mathsf {LinHC}$ protocol. Due to page limitation, below we only remark on one of the recent lattice-based protocols. We provide further discussion in the full version for the rest of the protocols: proof of opening of commitments [3], one-out-of-many proofs [15], exact sound proofs for quadratic relations [35], and product proofs for commitments [1].

[15]: Range proofs. Range proof allows one to prove that a committed value resides in a specific range and is used in applications such as confidential transactions in cryptocurrencies. Recently, Esgin et al. [15] provided an efficient range proof by using new ideas on CRT-packing supporting “inter-slot” operations and NTT-friendly tools that permit the use of fully-splitting rings. It can be checked that the $\varSigma$-protocol for the range relation provided in [15, Theorem 1] is compatible with extractable $\mathsf {LinHC}$ protocols. Although it was not necessary for their scheme, we can modify the verifier in [15, Protocol 2] (without affecting any parameters) to further check the bound on $\boldsymbol{f}_{\mathrm {crt}}$ to perfectly fit the description of the extractable $\mathsf {LinHC}$ protocol. Concretely, we can view $(a_j^{i})_{(i, j) \in [\psi , k_i - 1]}, \boldsymbol{r}_a, \boldsymbol{r}_d$, and $\boldsymbol{r}_e$ in their Protocol 2 as $\mathbf {r}$, and $(b_j^{i})_{(i, j) \in [\psi , k_i - 1]}, \boldsymbol{r}_b, \boldsymbol{r}_c$, and $\boldsymbol{r}$ in their Protocol 2 as $\mathbf {e}$ of the extractable $\mathsf {LinHC}$ protocol in our Fig. 1.

Finally, we elucidate an inconvenient feature of some of the recent advanced lattice-based protocols. While conventional protocols only require 2 to 3 valid transcripts for special soundness, as much as 32 valid transcripts is required in the recent protocols [1]. Therefore, even if the protocols came with a compatible lossy function as in the definition of [25], the Fiat-Shamir transform incurs an extremely large reduction loss. Combining [14, Lemma 29] and [25, Theorem 1], a knowledge extractor (for the underlying protocol) given black-box access to a quantum adversary outputting a valid $\mathsf{NIZK}$ proof with probability $\epsilon$ after making Q hash queries, is only guaranteed in extracting a witness with probability $(\epsilon /Q^2)^{2\times 32-1} = \epsilon ^{63}/Q^{126}$. In such cases, extractable $\mathsf {LinHC}$ protocols may provide a much tighter proof and a smaller set of provably secure parameters.