The regularization of spectral methods for hyperbolic Volterra integrodifferential equations with fractional power elliptic operator

F. Mirzaei G.; Davood Rostamy

doi:10.1515/nleng-2022-0250

Open Access Published by De Gruyter February 8, 2023

The regularization of spectral methods for hyperbolic Volterra integrodifferential equations with fractional power elliptic operator

F. Mirzaei G. and Davood Rostamy

From the journal Nonlinear Engineering

https://doi.org/10.1515/nleng-2022-0250

Abstract

In this study, a numerical approach is presented to solve the linear and nonlinear hyperbolic Volterra integrodifferential equations (HVIDEs). The regularization of a Legendre-collocation spectral method is applied for solving HVIDE of the second kind, with the time and space variables on the basis of Legendre-Gauss-Lobatto and Legendre-Gauss (LG) interpolation points, respectively. Concerning bounded domains, the provided HVIDE relation is transformed into three corresponding relations. Hence, a Legendre-collocation spectral approach is applied for solving this equation, and finally, ill-posed linear and nonlinear systems of algebraic equations are obtained; therefore different regularization methods are used to solve them. For an unbounded domain, a suitable mapping to convert the problem on a bounded domain is used and then apply the same proposed method for the bounded domain. For the two cases, the numerical results confirm the exponential convergence rate. The findings of this study are unprecedented for the regularization of the spectral method for the hyperbolic integrodifferential equation. The result in this work seems to be the first successful for the regularization of spectral method for the hyperbolic integrodifferential equation.

Keywords: hyperbolic Volterra integrodifferential equations; Legendre-collocation spectral method; regularization methods; Gauss quadrature formulas; differentiation matrix

1 Introduction

This article considers the following hyperbolic Volterra integrodifferential equations (HVIDEs):

(1.1) U t t + A α U − λ α , β ∫ 0 t K ( t − s ) A β U ( ⋅ , s ) d s = F , 0 < α , β ≤ 1 , in Ω × ( 0 , T ] , U = 0 , on ∂ Ω × ( 0 , T ] , U ( ⋅ , 0 ) = U 0 , U t ( ⋅ , 0 ) = U 1 in Ω ,

where Ω is a domain in R d and U = U ( x , t ) that x = ( x , y ) ∈ Ω , with boundary ∂ Ω . The function F and the initial functions U 0 and U 1 are sufficiently smooth. Here, A U ≔ △ U + c ( x ) U is a self-adjoint, positive definite uniformly elliptic second-order operator on a Hilbert space if c ( x ) ≥ 0 (cf. [1]). The kernel K is considered to be smooth (exponential) with the following properties:

(1.2) K ≥ 0 , K ′ ≤ 0 , and ‖ K ‖ L 1 [ Ω × ( 0 , T ] ] < 1 .

The integrodifferential equation (1.1) can be realized as integrodifferential partial differential equations arising from the theory of viscoelasticity (see [2]), and the above abstract model applies to a large variety of elastic systems, which describe the process of heat propagation in media with memory at a finite rate, where u = u ( x , t ) ∈ R 3 represents the displacement vector of a viscoelastic isotropic hereditary medium. Indeed, experience confirms that the behavior of some viscoelastic materials (polymers, suspensions, and emulsions) shows memory properties. Consequently, in the constitutive assumptions, stress depends not only on the present values of the strain and/or velocity gradient but also on the entire temporal history of the motion as well. Typically, memory fades with time: disturbances that occurred in the recent past have a greater influence on the present stress than those in the distant past. For these motivations, many constitutive models for viscoelastic materials lead to equations of motion that have the form of a linear hyperbolic partial differential equation perturbed by a dissipative integral term of Volterra type, having a nonnegative, decreasing convolution kernel, see, e.g., refs [3–6].

The problem (1.1) with smooth kernels has been studied in previous studies [7–10] for special case α = β = 1 , where they showed the existence and uniqueness of solutions for smooth initial data using energy estimates. In the study of Hrusa and Renardy [11], the existence of a discontinuous solution was shown for non-smooth initial data. Galerkin approximate solutions of (1.1) with weakly singular kernels have been discussed in the study by Choi and Macamy [12], in which error estimates are given for the semi-discrete scheme. The super-convergence estimates for this class of problem have been studied by Lin et al. [13], for error estimates of backward Euler’s fully discrete spectral approximate solutions for (1.1) with a weakly singular kernel has been studied by Chung and Park [14].

For the numerical approach of (1.1), local and global weak solutions of (1.1) with singular kernels have been achieved by Engler [15]. We observe that Rothe’s method has been studied Lin et al. [13]. An hp-discontinuous Galerkin method is applied for problem (1.1) in the study by Karaa et al. [16] and a symmetric finite volume element method is utilized to resolve problem (1.1) in the study by Gan and Yin [17]. In addition, a Galerkin approach on the basis of least squares is proposed [18]. On the other hand, we observe that a huge class of methods for solving hyperbolic and parabolic Volterra integral equations are proposed [19].

The numerical methods considered in this article will be obtained by a new Legendre-collocation spectral method. Spectral method has excellent error properties, with “exponential convergence” being the fastest possible. This, along with the ease of applying these methods to infinite domains, has encouraged many authors to use them for various equations. Specific types of spectral methods that are more applicable and extensively utilized are collocation methods. More information about these methods can be found in previous studies [20–26]. Tang and Mab [27] developed a Legendre-collocation spectral method in time with regard to the first-order hyperbolic equations for the Volterra integral equations [28], and Jiang [29] developed a Legendre-collocation spectral method for Volterra integrodifferential equations (VIDEs) with the smooth kernels is analyzed, for a class of VIDEs with the noncompact integral operator [30]. In addition, as for neutral and high-order VIDEs with a regular kernel, the readers are referred to the study by refs [1,2,25,31,32]; as for the numerical treatment of Fredholm integrodifferential-difference equations, including variable coefficients, the readers are referred to the study by Sahu and SahaRay [33], Sumudu Lagrange-spectral methods for solving systems of linear and nonlinear Volterra integrodifferential equations [34]; and refer to the study by Wei and Chen [35] for Volterra-Hammerstein integral equation with a regular kernel.

This study aims to provide a hybrid spatial numerical method for HVIDEs by a fully spectral method based on the Legendre-collocation approximation of both space and time variables and extended regularization approaches for ill-posed problems.

The following motivations arise when studying (1.1).

To simplify a numerical solution with more dimensions than 1, we could use the proposed method to reduce the problem to one dimension, then use a suitable numerical method to solve it.
Hyperbolic problems are of ill-posed problems, which is transformed to ill-condition using spectral methods. In this article, we proposed a powerful spectral hybrid method with suitable errors for the solution of ill-posed linear system.

The remainder of this article is presented as follows. Section 2 provides some preliminaries and properties of Legendre and Lagrange polynomials. In Section 3, we develop a regularization spectral approach to create an algorithm to address the inverse issues pertaining to HVIDEs under Dirichlet and Neumann boundary states on bounded and unbounded domains. In Section 4, we investigate several numerical examples to illustrate the performance and efficiency of the proposed methods. The article ends with some conclusions and observations in Section 5.

2 Legendre and Lagrange polynomials and their properties

The well-known Legendre polynomials P k ( x ) are defined within interval [ − 1 , 1 ] . First, some properties of the standard Legendre polynomials are utilized for this section. The Legendre polynomials P k ( x ) ( k = 0 , 1 , … ) satisfy the following Rodrigues formula:

P k ( x ) = ( − 1 ) k 2 k k ! D k ( ( 1 − x 2 ) k ) .

In addition, P k ( x ) is a polynomial of degree k . The Legendre polynomials satisfy the following equations:

P 0 ( x ) = 1 , P 1 ( x ) = 1 , P k + 1 ( x ) = 2 k + 1 k + 1 x P k ( x ) − k k + 1 P k − 1 ( x ) , k = 1 , 2 , … x ∈ [ − 1 , 1 ] .

Moreover, they are orthogonal in regard to L 2 inner product on the interval [ − 1 , 1 ] and the following orthogonality relation:

( P n ( x ) , P m ( x ) ) ω = ∫ − 1 1 P n ( x ) P m ( x ) ω ( x ) = 2 2 n + 1 δ n m ,

where ω ( x ) = 1 and δ n m is the Kronecker delta. The Legendre-Gauss (LG) quadrature formula is presented as follows:

∫ − 1 1 f ( x ) ω ( x ) d x = ∑ i = 0 N f ( x i ) ω i .

We assume the LG points { x i } i = 0 N , i.e., the roots of P N + 1 ( x ) = 0 such that P N + 1 is the ( N + 1 ) th Legendre polynomial and ω i are the corresponding weights defined as follows:

ω i = 2 ( 1 − x i 2 ) ( P N + 1 ′ ( x i ) ) 2 , i = 0 , … , N .

For more details about Legendre polynomials, see ref. [36].

All function u ( x ) defined over [ a , b ] can be approximated by Lagrange interpolation polynomials. So, we have

(2.1) u N ( x ) ≈ I N ( x ) = ∑ j = 0 N u ( x j ) L j ( x ) ,

with u j = u ( x j ) , where x j , j = 0 , 1 , … , N are interpolating points that satisfy a ≤ x 0 < x 1 < … < x N − 1 < x N ≤ b and

L j ( x ) = 1 c j ∏ i = 0 , i ≠ j N ( x − x i ) , 0 ≤ j ≤ N , c j ( x ) = ∏ i = 0 , i ≠ j N ( x j − x i ) ,

as well as

L j ( x i ) = δ j i = 0 , i ≠ j , 1 , i = j .

The reader is referred to ref. [36] for more details about these functions and their properties. For computing the first derivative of Eq. (2.1) at x k , we can denote

d d x I N ( x ) = ∑ j = 0 N d k j u ( x j ) = D u ,

where u k = I N ( x k ) and D = [ d k j ] = [ L j ′ ( x k ) ] . To derive the entries of the differentiation matrix D ,

d k j = c k c j ( x k − x j ) − 1 , k ≠ j , − ∑ j = 0 , j ≠ k N d k j , k = j ,

such that c k = ∏ l = 0 , l ≠ k N ( x k − x l ) . The computation of ratio c k c j in d k j may enable round-off error; hence, to avoid this problem, we can compute them as follows:

c k c j = ( − 1 ) k + j e b k − b j , b k = ∑ l = 0 , l ≠ k N ln ∣ x k − x l ∣ .

Now the entries of matrix D ( 2 ) = [ d k j ( 2 ) ] = [ L j ″ ( x k ) ] can be performed by the entries of D recursively, and we obtain

d k j ( 2 ) = 2 ( d k k d k j − ( x k − x j ) − 1 d k j ) , k ≠ j , − ∑ j = 0 , j ≠ k N d k j ( 2 ) , k = j .

By taking the first and second derivatives, we have general Lagrangian interpolation polynomials (for see more ref. [37]).

3 Implementation of Legendre-collocation spectral method

For this section, the fundamental Legendre-collocation spectral approach is presented to resolve the integrodifferential relations determined in Eq. (1.1) on bounded domain Ω = [ − 1 , 1 ] × [ − 1 , 1 ] and unbounded domain Ω = ( − ∞ , ∞ ) × ( − ∞ , ∞ ) . For this approximation process, the LG quadrature rule and the Lagrange interpolation polynomials are implemented.

3.1 Change of variables for two-dimensional of Eq. (1.1)

We consider the two-dimensional of Eq. (1.1). For convenience, we provide formulas for every first-, and second-order derivatives u ( z , t ) ≔ U ( x , y , t ) of two variables, where z = x 2 + y 2 ∈ R 2 and r = z − 1 . The chain rule of differentiations implies

∂ U ∂ t = ∂ u ∂ t , ∂ U ∂ x = x z ∂ u ∂ z ,

and similarly, ∂ U ∂ y = y z ∂ u ∂ z . The generic second-order derivatives are given as follows:

∂ 2 U ∂ t 2 = ∂ 2 u ∂ t 2 , ∂ 2 U ∂ x 2 = x 2 z 2 ∂ 2 u ∂ z 2 + y 2 z 3 ∂ u ∂ z ,

as well as

∂ 2 U ∂ y 2 = y 2 z 2 ∂ 2 u ∂ z 2 + x 2 z 3 ∂ u ∂ z ,

and for the Laplacian or

A U ≔ ∂ 2 U ∂ x 2 + ∂ 2 U ∂ y 2 + c ( x , y ) U = ∂ 2 u ∂ z 2 + 1 z ∂ u ∂ z + c ( z ) u .

Therefore, Eq. (1.1) represents:

(3.1) ∂ 2 u ( z , t ) ∂ t 2 + ∂ 2 u ( z , t ) ∂ z 2 + 1 z ∂ u ( z , t ) ∂ z + C ( z ) u ( z , t ) α − λ α , β ∫ 0 t K ( t − s ) ∂ 2 u ( z , s ) ∂ z 2 + 1 z ∂ u ( z , s ) ∂ z C ( z ) u ( z , s ) β d s = f ( z , t ) , in Ω × ( 0 , T ] , u ( z , t ) = 0 , on ∂ Ω × ( 0 , T ] , u ( ⋅ , 0 ) = u 0 , u t ( ⋅ , 0 ) = u 1 , in Ω ,

that

u 1 ( z , t ) ≔ U 1 ( x , y , 0 ) , f ( z , t ) ≔ F ( x , y , t ) .

The problem (3.1) is assumed on the bounded domain Ω = [ 0 , 2 ] . First, we will transfer (3.1) from Ω = [ 0 , 2 ] to an equivalent problem defined in [ − 1 , 1 ] as follows:

(3.2) ∂ 2 u ( r , t ) ∂ t 2 + ∂ 2 u ( r , t ) ∂ r 2 + 1 r + 1 ∂ u ( r , t ) ∂ r + C ( r ) u ( r , t ) α − λ α , β ∫ 0 t K ( t − s ) ∂ 2 u ( r , s ) ∂ r 2 + 1 r + 1 ∂ u ( r , s ) ∂ r + C ( r ) u ( r , s ) β d s = f ( r , t ) , in Ξ × ( 0 , T ] , u ( r , t ) = 0 , on ∂ Ξ × ( 0 , T ] , u ( ⋅ , 0 ) = u 0 , u t ( ⋅ , 0 ) = u 1 , in Ξ ,

where f ( r , t ) ≔ F ( x , y , t ) , c ( z ) ≔ C ( r ) , and Ω is transformed to Ξ . Concerning a bounded domain, without loss of generality, we assume that Ξ = [ − 1 , 1 ] and, for unbounded domain, Ξ = R is assumed.

3.2 Bounded domain

Before using collocation methods, we need to restate problem (3.2) for applying the theory based on Legendre expansions on the finite interval [ − 1 , 1 ] . If we consider

t = T ( τ + 1 ) 2 , τ ∈ [ − 1 , 1 ] ,

then we have

(3.3) 4 T 2 ∂ 2 v ∂ τ 2 + ∂ 2 v ∂ r 2 + 1 r + 1 ∂ v ∂ r + C ( r ) v ( r , τ ) α − λ α , β ∫ 0 T ( τ + 1 ) 2 K T ( τ + 1 ) 2 − s ∂ 2 v ∂ r 2 + 1 r + 1 ∂ v ∂ r + C ( r ) v ( r , τ ) β d s = g ( r , τ ) , r , τ ∈ [ − 1 , 1 ] , v ( r , t ) = 0 , r ∈ [ − 1 , 1 ] , v ( ⋅ , 0 ) = v 0 , v τ ( ⋅ , 0 ) = T 2 v 1 , r ∈ ( − 1 , 1 ) ,

where we have

v ( r , τ ) ≔ u r , T ( τ + 1 ) 2 , v 0 ( r , 0 ) ≔ u 0 ( r , 0 ) , v 1 ( r , 0 ) ≔ u 1 ( r , 0 ) , g ( r , τ ) ≔ f r , T ( τ + 1 ) 2 .

Furthermore, the integral interval 0 , T ( τ + 1 ) 2 is transferred to the interval [ − 1 , τ ] , making a linear transformation as follows:

s = T ( y + 1 ) 2 , y ∈ [ − 1 , τ ] .

Then, Eq. (3.3) turns into

(3.4) 4 T 2 ∂ 2 v ( r , τ ) ∂ τ 2 + ∂ 2 v ( r , τ ) ∂ r 2 + 1 r + 1 ∂ v ( r , τ ) ∂ r + C ( r ) v ( r , τ ) α − λ α , β T 2 ∫ − 1 τ k ( τ − y ) ∂ 2 v ( r , y ) ∂ r 2 + 1 r + 1 ∂ v ( r , y ) ∂ r + C ( r ) v ( r , y ) β d y = g ( r , τ ) ,

where k ( T ( τ − y ) ) ≔ K T ( 1 + τ ) 2 − T ( y + 1 ) 2 . Now, we integrate the above equation on the interval [ − 1 , τ ] and we obtain

(3.5) 4 T 2 ( v τ ( r , τ ) − v τ ( r , − 1 ) ) + ∫ − 1 τ ∂ 2 v ( r , μ ) ∂ r 2 + 1 r + 1 ∂ v ( r , μ ) ∂ r + C ( r ) v ( r , μ ) α d μ − T λ α , β 2 ∫ − 1 τ ∫ − 1 μ k ( μ − y ) ∂ 2 v ( r , y ) ∂ r 2 + 1 r + 1 ∂ v ( r , y ) ∂ r + C ( r ) v ( r , y ) β d y d μ = ∫ − 1 τ g ( r , μ ) d μ , τ ∈ [ − 1 , 1 ] .

For simplicity in calculation, we consider the following auxiliary function z ( x , τ ) .

(3.6) z ( r , τ ) = g ( r , τ ) + T λ α , β 2 ∫ − 1 τ k ( τ − y ) × ∂ 2 v ( r , y ) ∂ r 2 + 1 r + 1 ∂ v ( r , y ) ∂ r + C ( r ) v ( r , y ) β d y .

Hence, Eq. (3.5) can be converted to the following new form:

(3.7) v τ ( r , τ ) = v τ ( r , − 1 ) + T 2 4 ∫ − 1 τ ( z ( r , μ ) − v r r ( r , μ ) + 1 r + 1 v r ( r , μ ) + C ( r ) v ( r , μ ) α d μ .

Again, integrating Eq. (3.7) on the interval [ − 1 , τ ] , we have

(3.8) v ( r , τ ) = v 0 + T 2 V 0 ( τ + 1 ) + T 2 4 ∫ − 1 τ ∫ − 1 ρ ( z ( r , κ ) − v r r ( r , κ ) + 1 r + 1 v r ( r , κ ) + C ( r ) v ( r , κ ) α d κ d μ .

Then, definite

(3.9) H ( r , τ ) = T 2 ∫ − 1 τ ( z ( r , μ ) − ( v r r ( r , μ ) + 1 r + 1 v r ( r , μ ) + C ( r ) v ( r , μ ) α d μ ,

where we again consider the auxiliary function H ( x , τ ) . Hence, we can write Eq. (3.8) as follows:

(3.10) v ( r , τ ) = v 0 + T 2 v 1 ( τ + 1 ) + T 2 ∫ − 1 τ H ( r , μ ) d μ .

Denote the collocation points { ( r j , τ i ) } j , i = 0 N , M be the set of Legendre-Gauss-Lobatto (LGL) and LG collocation points, respectively. A first approximation to Eqs (3.6), (3.9), and (3.10) using a Legendre collocation approach is

(3.11) z ( r j , τ i ) = g ( r j , τ i ) + T λ α , β 2 ∫ − 1 τ i k ( τ i − y ) × ( v r r ( r j , y ) + 1 r j + 1 v r ( r j , y ) + C ( r j ) v ( r j , y ) β d y , 0 ≤ j ≤ N , 0 ≤ i ≤ M ,

(3.12) H ( r j , τ i ) = T 2 ∫ − 1 τ i ( z ( r j , μ ) − ( v r r ( r j , μ ) + 1 r j + 1 v r ( r j , μ ) + C ( r j ) v ( r j , μ ) α d μ , 0 ≤ j ≤ N , 0 ≤ i ≤ M ,

(3.13) v ( r j , τ i ) = v 0 ( r j ) + T 2 v 1 ( r j ) ( τ i + 1 ) + T 2 ∫ − 1 τ i H ( r j , μ ) d μ , 1 ≤ j ≤ N − 1 , 0 ≤ i ≤ M .

A prominent issue in acquiring high-order precision is the accurate derivation of the integral term in Eqs (3.11)–(3.13). Particularly, in regard to small values of ( r j , τ i ) , there is little information available. For the purpose of overcoming such issue, we convert the integral interval [ − 1 , τ i ] to [ − 1 , 1 ] , and hence the Gaussian-type quadrature rule is applied to approximate the integral. More precisely, we use the following linear transformation:

(3.14) μ ( τ i , θ ) = y ( τ i , θ ) = τ i + 1 2 θ + τ i − 1 2 , θ ∈ [ − 1 , 1 ] .

Then, Eqs (3.11)–(3.15) can be reduced as follows:

(3.15) z ( r j , τ i ) = g ( r j , τ i ) + T λ α , β ( τ i + 1 ) 4 × ∫ − 1 1 k ( τ i − y ( τ i , θ ) ) ( v r r ( r j , y ( τ i , θ ) ) + 1 r j + 1 v r ( r j , y ( τ i , θ ) ) + C ( r j ) v ( r j , y ( τ i , θ ) ) β d θ ,

(3.16) H ( r j , τ i ) = T ( τ i + 1 ) 4 ∫ − 1 1 z ( r j , μ ( τ i , θ ) ) − v r r ( r j , μ ( τ i , θ ) ) + 1 r j + 1 v r ( r j , μ ( τ i , θ ) ) + C ( r j ) v ( r j , μ ( τ i , θ ) ) α d θ ,

(3.17) v ( r j , τ i ) = v 0 ( r j ) + T 2 v 1 ( r j ) ( τ i + 1 ) + T ( τ i + 1 ) 4 ∫ − 1 1 H ( r j , μ ( τ i , θ ) ) d θ .

By applying the ( p + 1 ) -point LG-type quadrature formula, using the notes and weights represented via { θ k , w k } k = 0 p , we estimate the integral to obtain

(3.18) z ( r j , τ i ) ≈ g ( r j , τ i ) + T λ α , β ( τ i + 1 ) 4 ∑ k = 0 p k ( τ i − y ( τ i , θ k ) ) × v r r ( r j , y ( τ i , θ k ) ) + 1 r j + 1 v r ( r j , y ( τ i , θ k ) ) + C ( r j ) v ( r j , y ( τ i , θ k ) ) β w k ,

(3.19) H ( r j , τ i ) ≈ T ( τ i + 1 ) 4 ∑ k = 0 p z ( r j , μ ( τ i , θ k ) ) − v r r ( r j , μ ( τ i , θ k ) ) + 1 r j + 1 v r ( r j , μ ( τ i , θ k ) ) + C ( r j ) v ( r j , μ ( τ i , θ k ) ) α w k ,

(3.20) v ( r j , τ i ) ≈ v 0 ( r j ) + T 2 v 1 ( r j ) ( τ i + 1 ) + T ( τ i + 1 ) 4 ∑ k = 0 p H ( r j , μ ( τ i , θ k ) ) w k .

We consider approximation solutions as follows:

z ( r , τ ) ≈ I N M z ( r , τ ) = ∑ n = 0 N ∑ m = 0 M l n ( r ) ρ m ( τ ) z ( r n , τ m ) ,

H ( r , τ ) ≈ I N M H ( r , τ ) = ∑ n = 0 N ∑ m = 0 M l n ( r ) ρ m ( τ ) H ( r n , τ m ) ,

v ( r , τ ) ≈ I N M v ( r , τ ) = ∑ n = 0 N ∑ m = 0 M l n ( r ) ρ m ( τ ) v ( r n , τ m ) ,

where l n and ρ m are the n -th and m -th Lagrange interpolation polynomials based on the grid points { r n } n = 0 N , { τ m } m = 0 M , respectively. By imposing the boundary conditions in the interpolation polynomial of v , we have

(3.21) v ( r , τ ) ≈ I N M v ( r , τ ) = ∑ n = 1 N − 1 ∑ m = 0 M l n ( r ) ρ m ( τ ) v ( r n , τ m ) .

By applying the interpolation polynomial v of Eq. (3.21), we can expand v r and v r r in Eqs (3.18) and (3.19) as follows:

(3.22) v r ( r , τ ) ≈ ∂ I N M v ( r , τ ) ∂ r = ∑ n = 1 N − 1 ∑ m = 0 M l n ′ ( r ) ρ m ( τ ) v ( r n , τ m ) ,

(3.23) v r r ( r , τ ) ≈ ∂ 2 I N M v ( r , τ ) ∂ r 2 = ∑ n = 1 N − 1 ∑ m = 0 M l n ″ ( r ) ρ m ( τ ) v ( r n , τ m ) .

Substituting these approximations Eqs (3.21)–(3.23) into Eqs (3.18)–(3.20) yield

(3.24) z ( r j , τ i ) ≈ g ( r j , τ i ) + T λ α , β ( τ i + 1 ) 4 ∑ k = 0 p k ( τ i − y ( τ i , θ k ) ) × ∂ 2 I N M v ( r , y ( τ i , θ k ) ) ∂ r 2 r = r j + 1 r + 1 ∂ I N M v ( r , y ( τ i , θ k ) ) ∂ r r = r j + C ( r ) I N M v ( r , y ( τ i , θ k ) ) ∣ r = r j β w k ,

(3.25) H ( r j , τ i ) ≈ T ( τ i + 1 ) 4 × ∑ k = 0 p I N M z ( r j , μ ( τ i , θ k ) ) + ∂ 2 I N M v ( r , μ ( τ i , θ k ) ) ∂ r 2 r = r j + 1 r + 1 ∂ I N M v ( r , μ ( τ i , θ k ) ) ∂ r r = r j + C ( r ) I N M v ( r , μ ( τ i , θ k ) ) ∣ r = r j ) α ) w k ,

(3.26) v ( r j , τ i ) ≈ v 0 ( r j ) + T 2 v 1 ( r j ) ( τ i + 1 ) + T ( τ i + 1 ) 4 ∑ k = 0 p I N M H ( r j , μ ( τ i , θ k ) ) w k ,

where

∂ I N M v ( r , μ ( τ i , θ k ) ) ∂ r r = r j = ∑ n = 1 N − 1 ∑ m = 0 M d n j ρ m ( μ ( τ i , θ k ) ) v ( r n , τ m ) ,

∂ 2 I N M v ( r , μ ( τ i , θ k ) ) ∂ r 2 r = r j = ∑ n = 1 N − 1 ∑ m = 0 M d n j ( 2 ) ρ m ( μ ( τ i , θ k ) ) v ( r n , τ m ) .

To make it easier to solve, Eqs (3.24)–(3.26) can be written in matrix form. Therefore, we denote V j , i , H j , i , and Z j , i be the approximation of v ( r j , τ i ) , H ( r j , τ i ) , and z ( r j , τ i ) , respectively. So, we define matrix forms as in the following:

V N − 2 M = vec [ V j , i ] , 1 ≤ j ≤ N − 1 , 1 ≤ i ≤ M + 1 , Z N M = vec [ Z j , i ] , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ M + 1 , H N M = vec [ H j , i ] , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ M + 1 , G N M = vec [ G ( r j , τ i ) ] , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ M + 1 ,

where the vec operator transforms a matrix to a vector via the placement of matrix rows below one other starting from the first to the last. By forcing the initial value at t = 0 , we denote

IVP = vec v ( r 1 , 0 ) + T 2 v 1 ( r 1 , 0 ) ( τ 1 + 1 ) ⋯ v ( r 1 , 0 ) + T 2 v 1 ( r 1 , 0 ) ( τ M + 1 + 1 ) v ( r 2 , 0 ) + T 2 v 1 ( r 2 , 0 ) ( τ 1 + 1 ) ⋯ v ( r 1 , 0 ) + T 2 v 1 ( r 2 , 0 ) ( τ M + 1 + 1 ) ⋮ ⋮ ⋮ v ( r N − 1 , 0 ) + T 2 v 1 ( r N − 1 , 0 ) ( τ 1 + 1 ) ⋯ v ( r N − 1 , 0 ) + T 2 v 1 ( r N − 1 , 0 ) ( τ M + 1 + 1 ) ( N − 1 ) × ( M + 1 ) .

Then, the linear and nonlinear system Eqs (3.24)–(3.26) reduce to the following matrix forms:

(3.27) Z ( N + 1 ) ( M + 1 ) = G ( N + 1 ) ( M + 1 ) + ( T + B + C j ) β V ( N − 1 ) ( M + 1 ) ,

(3.28) H ( N + 1 ) ( M + 1 ) = C Z ( N + 1 ) ( M + 1 ) + ( E + F + C j ) α V ( N − 1 ) ( M + 1 ) ,

(3.29) V ( N − 1 ) ( M + 1 ) = IVP + D H ( N + 1 ) ( M + 1 ) ,

where we define, for all 1 ≤ m , n ≤ M + 1 , T = ( T j i ) j , i , B = ( B j i ) j , i , C = ( C j i ) j , i , E = ( E j i ) j , i , F = ( F j i ) j , i , and D = ( D j i ) j , i , are block matrices. That each j , i , T j i , and B j i are matrices with dimension of ( N + 1 ) × ( N − 1 ) , where the entries of matrices ( T + B ) j i are determined as follows:

( T j i ) n , m = d ( j ) ( i + 1 ) ( 2 ) ∑ k = 0 p T λ α , β ( τ n + 1 ) 4 K × ( τ n − y ( τ n , θ k ) ) ρ m ( y ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ N − 1 ,

and

( B j i ) n , m = d ( j ) ( i + 1 ) ( r j + 1 ) ∑ k = 0 p T λ α , β ( τ n + 1 ) 4 K × ( τ n − y ( τ n , θ k ) ) ρ m ( y ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ N − 1 .

Similar to T = ( T j i ) j , i and B = ( B j i ) j , i , for each j and i , E j i and F j i are matrices with dimension of ( N + 1 ) × ( N − 1 ) , which the entries of matrices ( E + F ) j i are given as follows:

( E j i ) n , m = − ∑ k = 0 p T ( τ n + 1 ) 4 d ( j ) ( i + 1 ) ( 2 ) ρ m ( μ ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ N − 1 ,

and

( F j i ) n , m = − 1 ( r j + 1 ) ∑ k = 0 p T ( τ n + 1 ) 4 d ( j ) ( i + 1 ) ρ j ( μ ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ N − 1 .

Similarly, the C j i is a diagonal matrix with dimension of ( N + 1 ) × ( N + 1 ) .

( C j j ) n , m = ∑ k = 0 p T ( τ n + 1 ) 4 ρ m ( μ ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 .

Finally, D j i is a matrix with dimension of ( N − 1 ) × ( N + 1 ) , where the first and last columns in it are zero and other elements are provided by

( D j j ) n , m = ∑ k = 0 p T ( τ n + 1 ) 4 ρ m ( μ ( τ n , θ k ) ) w k , 1 ≤ j ≤ N − 1 ,

where, regardless of the first and last columns, D j i is a diagonal matrix.

Finally, the linear and nonlinear algebraic systems of the matrix form Eqs (3.27)–(3.29) reduce to

(3.30) ( I − D C ( T + B + C j ) β − D ( E + F + C j ) α ) V ( N − 2 ) M = IVP + D C G N M .

By solving (3.30) with the aforementioned methods, the problem has become an ill-posed problem. Hence, we may, by selecting one of regularization methods, treat an ill-posed problem to a well-posed problem. The matrix form (3.30) could be simplified to the standard form

(3.31) A 1 X = B 1 , A 1 ∈ R m × n , X 1 ∈ R n , B 1 ∈ R m ,

using a large matrix A 1 of ill-determined rank. Specifically, A 1 is severely ill-conditioned and can be singular, where we have

A 1 ≔ ( I − D C ( T + B + C j ) β − D ( E + F + C j ) α ) , X 1 ≔ V ( N − 2 ) M , B 1 ≔ IV P + D C G N M .

3.3 Unbounded domain

By taking the following initial boundary-value equation into consideration on Ω = R 2 ,

(3.32) U t t + A α U − λ α , β ∫ 0 t K ( t − s ) A β U ( ⋅ , s ) d s = F , 0 < α , β ≤ 1 , ( x , y ) ∈ R 2 , t ∈ ( 0 , T ] , U ( ⋅ , 0 ) = U 0 , U t ( ⋅ , 0 ) = U 1 , U → 0 as ∣ ( x , y ) ∣ → ∞ .

Therefore, by using (3.2), we have the following equation:

(3.33) ∂ 2 u ∂ t 2 + ∂ 2 u ∂ r 2 + 1 r + 1 ∂ u ∂ r + C ( r ) u α − λ α , β ∫ 0 t K ( t − s ) ( ∂ 2 u ∂ r 2 + 1 r + 1 ∂ u ∂ r + C ( r ) u ) β d s = f ( r , t ) , r ∈ R , t ∈ ( 0 , T ] , u ( ⋅ , 0 ) = u 0 , u t ( ⋅ , 0 ) = u 1 , u → 0 as ∣ r ∣ → ∞ .

Among numerous common mappings that project unbounded and bounded domains to one another, more practical forms of mappings, such as algebraic, logarithmic, and exponential, are of more applicability (for more details, see [38], p. 280). Now, using the algebraic mapping h : ( − 1 , 1 ) → ( − ∞ , + ∞ ) , with positive scaling parameter L ,

h ( r ) = L r 1 − r 2 ,

on (3.33), we obtain the following results:

(3.34) ∂ 2 v ∂ t 2 + 1 ( h ′ ( r ) ) 2 ∂ 2 v ∂ r 2 − h ″ ( r ) ( h ′ ( r ) ) 3 ∂ v ∂ r + 1 ( h ′ ( r ) ) 1 ( h ( r ) + 1 ) ∂ v ∂ r + C ( r ) v α − λ α , β ∫ 0 t K ( t − s ) 1 ( h ′ ( r ) ) 2 ∂ 2 v ∂ r 2 − h ″ ( r ) ( h ′ ( r ) ) 3 ∂ v ∂ r + 1 ( h ′ ( r ) ) 1 ( h ( r ) + 1 ) ∂ v ∂ r + C ( r ) v β d s = g ( r , t ) , in ( − 1 , 1 ) × ( 0 , T ] , v ( r , t ) → 0 , on r → ± 1 , v ( ⋅ , 0 ) = u 0 ( h ( r ) ) , u t ( ⋅ , 0 ) = v 1 ( h ( r ) ) , in ( − 1 , 1 ) ,

where v ( r , t ) ≔ u ( h ( r ) , t ) , v t ( r , t ) ≔ u 1 ( h ( r ) , t ) , and g ( r , t ) ≔ f ( h ( r ) , t ) . The following approach is similar to Section 3.2. So, for simplicity, Eq. (3.34) transforms the interval ( 0 , T ] to an equivalent problem defined in [ − 1 , 1 ] . Therefore, with defending the auxiliary functions Z ( r , τ ) and H ( r , τ ) , we restate (3.34) as follows:

(3.35) Z ( r j , τ i ) = G ( r j , τ i ) + T λ α , β ( τ i + 1 ) 4 × ∫ − 1 1 k ( τ i − y ( τ i , θ ) ) ( η j W r r ( r j , y ( τ i , θ ) ) + ( λ j − σ j ) W r ( r j , y ( τ i , θ ) ) + C ( r ) W ( r j , y ( τ i , θ ) ) ) β d θ ,

(3.36) H ( r j , τ i ) = T ( τ i + 1 ) 4 ∫ − 1 1 ( Z ( r j , μ ( τ i , θ ) ) − ( η j W r r ( r j , μ ( τ i , θ ) ) + ( λ j − σ j ) W r ( r j , μ ( τ i , θ ) ) ) + C ( r ) W ( r j , μ ( τ i , θ ) ) ) α d θ ,

(3.37) W ( r j , τ i ) = v 0 ( r j ) + T 2 v 1 ( r j ) ( τ i + 1 ) + T ( τ i + 1 ) 4 ∫ − 1 1 H ( r j , μ ( τ i , θ ) ) d θ ,

where, we consider points ( r j , τ i ) , that { r j } j = 0 N , and { τ i } i = 0 M are the LGL and LG points, respectively. We have

η j ≔ 1 ( h ′ ( r j ) ) 2 , σ j ≔ h ″ ( r j ) ( h ′ ( r j ) ) 3 , λ j ≔ 1 ( h ′ ( r j ) ) ( h ( r j ) + 1 )

and

W ( r , τ ) ≔ v r , T ( τ + 1 ) 2 , K ( r , τ − y ) ≔ k h ( r ) , T ( τ + 1 ) 2 − T ( y + 1 ) 2 , G ( r , τ ) ≔ g x , T ( τ + 1 ) 2 .

With approximating the integral part of Eqs (3.35)–(3.37), and for the purpose of using the ( p + 1 ) -point Gauss-Legendre quadrature formula, we obtain

(3.38) Z ( r j , τ i ) = G ( r j , τ i ) + T λ α , β ( τ i + 1 ) 4 ∑ k = 0 p k ( τ i − y ( τ i , θ ) ) × ( η j W r r ( r j , y ( τ i , θ ) ) + ( λ j − σ j ) W r ( r j , y ( τ i , θ ) ) + C ( r ) W ( r j , y ( τ i , θ ) ) ) β w k ,

(3.39) H ( r j , τ i ) = T ( τ i + 1 ) 4 ∑ k = 0 p ( Z ( r j , μ ( τ i , θ ) ) − ( η j W r r ( r j , μ ( τ i , θ ) ) + ( λ j − σ j ) W r ( r j , μ ( τ i , θ ) ) + C ( r ) W ( r j , μ ( τ i , θ ) ) ) α ) w k ,

(3.40) W ( r j , τ i ) = v 0 ( r j ) + T 2 v 1 ( r j ) ( τ i + 1 ) + T ( τ i + 1 ) 4 ∑ k = 0 p H ( r j , μ ( τ i , θ ) ) w k ,

where quadrature points { θ k } k = 0 p are roots of the ( p + 1 ) th Legendre polynomial. We consider non-uniform mesh { r j } j = 0 N by using the Lagrange interpolation polynomial of W and then the approximate solutions of W r r and W r . Thus, by expansion of Z , H , and W in Eqs (3.38)–(3.40), we achieve

(3.41) Z ( r j , τ i ) ≈ G ( r j , τ i ) + T λ α , β ( τ i + 1 ) 4 ∑ k = 0 p k ( τ i − y ( τ i , θ k ) ) × η j ∂ 2 I N M W ( r , y ( τ i , θ k ) ) ∂ r 2 r = r j + ( λ j − σ j ) ∂ I N M W ( r , y ( τ i , θ k ) ) ∂ r r = r j + C ( r ) W ( r j , μ ( τ i , θ ) ) ∣ r = r j β w k ,

(3.42) H ( r j , τ i ) ≈ T ( τ i + 1 ) 4 ∑ k = 0 p × I N M Z ( r j , μ ( τ i , θ k ) ) − η j ∂ 2 I N M W ( r , μ ( τ i , θ k ) ) ∂ r 2 r = r j + ( λ j + σ j ) ∂ I N M W ( r , μ ( τ i , θ k ) ) ∂ r r = r j + C ( r ) W ( r j , μ ( τ i , θ ) ) ∣ r = r j ) α ) w k ,

(3.43) W ( r j , τ i ) ≈ v 0 ( r j ) + T 2 v 1 ( r j ) ( τ i + 1 ) + T ( τ i + 1 ) 4 ∑ k = 0 p I N M H ( r j , μ ( τ i , θ k ) ) w k ,

where

∂ I N M W ( r , μ ( τ i , θ k ) ) ∂ r r = r j = ∑ n = 1 N − 1 ∑ m = 0 M d n j ρ m ( μ ( τ i , θ k ) v ( r n , τ m ) ) ,

∂ 2 I N M W ( r , μ ( τ i , θ k ) ) ∂ r 2 r = r j = ∑ n = 1 N − 1 ∑ m = 0 M d n j ( 2 ) ρ m ( μ ( τ i , θ k ) v ( r n , τ m ) ) .

In addition, after applying the homogeneous boundary conditions in (3.43), j differs from 1 to N − 1 . For the approximations of W ( r j , τ i ) , H ( r j , τ i ) , and Z ( r j , τ i ) , we denote the W j , i , H j , i , and Z j , i , respectively. Then, we denote vectors as follows:

W ( N − 1 ) ( M + 1 ) = vec [ W j , i ] , 1 ≤ j ≤ N − 1 , 1 ≤ i ≤ M + 1 ,

Z ( N + 1 ) ( M + 1 ) = vec [ Z j , i ] , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ M + 1 ,

H ( N + 1 ) ( M + 1 ) = vec [ H j , i ] , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ M + 1 ,

G ( N + 1 ) ( M + 1 ) = vec [ G ( r j , τ i ) ] , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ M + 1 ,

and after enforcing the initial condition, we have

IVP = vec v ( r 1 , 0 ) + T 2 v 1 ( r 1 , 0 ) ( τ 1 + 1 ) ⋯ v ( r 1 , 0 ) + T 2 v 1 ( r 1 , 0 ) ( τ M + 1 + 1 ) v ( r 2 , 0 ) + T 2 v 1 ( r 2 , 0 ) ( τ 1 + 1 ) ⋯ v ( r 2 , 0 ) + T 2 v 1 ( r 2 , 0 ) ( τ M + 1 + 1 ) ⋮ ⋮ ⋮ v ( r N − 1 , 0 ) + T 2 v 1 ( r N − 1 , 0 ) ( τ 1 + 1 ) ⋯ v ( r N − 1 , 0 ) + T 2 v 1 ( r N − 1 , 0 ) ( τ M + 1 + 1 ) ( N − 1 ) × ( M + 1 ) .

Therefore, we can define the matrix form of Eqs (3.41)–(3.43) as follows:

(3.44) Z ( N + 1 ) ( M + 1 ) = G ( N + 1 ) ( M + 1 ) + ( T + B + C j ) β W ( N − 1 ) ( M + 1 ) ,

(3.45) H ( N + 1 ) ( M + 1 ) = C Z ( N + 1 ) ( M + 1 ) + ( E + F + C j ) α W ( N − 1 ) ( M + 1 ) ,

(3.46) W ( N − 1 ) ( M + 1 ) = IVP + D H ( N + 1 ) ( M + 1 ) ,

where, for 1 ≤ n and m ≤ M + 1 , we define the block matrices T = ( T j i ) j , i , B = ( B j i ) j , i , C = ( C j i ) j , i , E = ( E j i ) j , i , F = ( F j i ) j , i , and D = ( D j i ) j , i . Now, we denote the entries of the matrices as follows:

( T j i ) n , m = η j d ( j ) ( i + 1 ) ( 2 ) ∑ k = 0 p T λ α , β ( τ n + 1 ) 4 K ( τ n − y ( τ n , θ k ) ) ρ m ( y ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ N − 1 ,

and

( B j i ) n , m = ( λ j − σ j ) d ( j ) ( i + 1 ) ∑ k = 0 p T λ α , β ( τ n + 1 ) 4 K ( τ n − y ( τ n , θ k ) ) × ρ m ( y ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ N − 1 ,

and similarly, we denote

( E j i ) n , m = − η j ∑ k = 0 p T ( τ n + 1 ) 4 d ( j ) ( i + 1 ) ( 2 ) ρ m ( y ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ N − 1 ,

and

( F j i ) n , m = − ( λ j − σ j ) ∑ k = 0 p T ( τ n + 1 ) 4 d ( j ) ( i + 1 ) ρ j ( y ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 , 1 ≤ i ≤ N − 1 ,

where, for each j and i , the T j i , B j i , E = ( E j i ) j , i , and F = ( F j i ) j , i are matrices with dimension of ( N + 1 ) × ( N − 1 ) and the C j i is a diagonal matrix with dimension of ( N + 1 ) × ( N + 1 ) such that its entries are determined as follows:

( C j j ) n , m = ∑ k = 0 p T ( τ n + 1 ) 4 ρ m ( μ ( τ n , θ k ) ) w k , 1 ≤ j ≤ N + 1 .

Finally, the D j i is a matrix with the dimension of ( N − 1 ) × ( N + 1 ) , where the first and last columns are zero and other its entries are achieved as follows:

( D j j ) n , m = ∑ k = 0 p T ( τ n + 1 ) 4 ρ m ( μ ( τ n , θ k ) ) w k , 1 ≤ j ≤ N − 1 .

Therefore, regardless of the first and last columns in D j i , it creates a diagonal matrix. By simplifying from Eqs (3.44)–(3.46), we only have to solve the linear and nonlinear algebraic systems shown below:

(3.47) ( I − D C ( T + B + C j ) β − D ( E + F + C j ) α ) W ( N − 2 ) M = IV P + D C G N M .

Similar to Section 3.2, by using the spectral methods, we arrive to the ill-posed linear and nonlinear systems. The linear and nonlinear systems of (3.47) are as follows:

(3.48) A 2 X 2 = B 2 , A 2 ∈ R m × n , X 2 ∈ R n , B 2 ∈ R m ,

with a large matrix A of ill-determined rank, where

A 2 ≔ ( I − D C ( T + B + C j ) β − D ( E + F + C j ) α ) , X 2 ≔ W ( N − 2 ) M , B 2 ≔ IV P + D C G N M .

3.4 Regularization formula for Eqs (3.30) and (3.47)

Discretization of the nonlinear and linear problems generally gives rise to very ill-posed nonlinear and linear systems of algebraic equations. Typically, the nonlinear and linear systems obtained have to be regularized to make the computation of a meaningful approximate solution possible. The discretization of the nonlinear and linear inverse problems typically gives rise to the nonlinear and linear systems of equations

(3.49) A i X i = B i , i = 1 , 2 ,

with a very ill-conditioned matrix A i of ill-determined rank. Deriving a meaningful approximate solution for the nonlinear and linear systems (3.31) generally necessitates the replacement of the system by a near system, which is not as sensitive to perturbations. Such replacement is known as regularization.

Tikhonov regularization is one of the most popular regularization methods, which replaces (3.49) by the minimization problem

(3.50) min X i ∈ R n { ‖ A i X i − B i ‖ 2 2 + μ i ‖ L i X i ‖ 2 2 } , i = 1 , 2 .

Here, the scalar μ i , i = 1 , 2 is a nonnegative real scalar, often referred to as the regularization parameter, and L i ∈ R k × n , k ≤ n , is a regularization operator; see [39] for discussions on Tikhonov regularization, and also we used of Tikhonov regularization based on the range restricted Arnoldi (RR-Arnoldi); see, e.g., ref. [40]. In this article, we use (range restricted-generalized minimal residual method) RR-GMRES iterative method to the solution of (3.49). RR-GMRES is better suited than standard GMRES for the computation of an approximate solution, which is of linear discrete ill-posed problems, of which desired solution x ˆ is smooth (for more details, see refs [41,42]).

Other regularization methods used for this article are the maximum entropy regularization method (Maxent). Such regularization method is commonly utilized in the image reconstruction field and in relevant applications where there is a need to seek a solution of positive elements. This method utilizes a nonlinear conjugate gradient algorithm, including inexact line search to derive regularized solutions; see (for more details see ref. [43] Chapter 4).

4 Applications and numerical results

For the following section, we first use the hybrid of regularization and Legendre-collocation spectral methods to solve the nonlinear and linear HVIDEs of the second kind for bounded and unbounded domains. Then, we illustrate the performance, efficiency, and accuracy of the regularization methods discussed with various numerical examples. Finally, let us look at all the examples in comparison to the regularization methods mentioned. We choose the approximating subspaces X N to be the Legendre polynomial subspaces of degree ≤ n . In all examples, we set parameters T = 1 and p = 20 . In addition, we call the following abbreviations for the used different schemes:

Exact Solution (ES),
Spectral Method (SM),
Regularization Spectral Methods (RSMs),
Tikhonove Regularization Spectral Method (TRSM),
Maxent Regularization Spectral Method (MRSM),
Arnoldi-Tikhonove Regularization Spectral Method (ATRSM),
RR-GMRS Regularization Spectral Method (RGRSM).

Tool box of MATLB are used in the following examples (see [44]). The numerical simulations are performed on a personal computer with a Core i 5 , 2.67 GHz CPU machine and 8 Gbyte of memory.

4.1 Bounded domain

In this section, we study the nonlinear and linear HVIDEs on bounded domain Ω = [ − 1 , 1 ] × [ − 1 , 1 ] , and the algorithms presented in Section 3 will be employed for solving this problem. For different values of N and M , the errors are given with L ∞ norms at the collocation points.

Example 4.1

As the first example, consider the problem HVIDEs with k ( x , y , t ) = e t and c ( x ) = 1 s i n ( π ( x 2 + y 2 ) ) . We investigate the problem for the linear HVIDEs when α = 1 and β = 1 . Therefore, so for nonlinear HVIDEs with α = 1 2 and β = 1 , f ( x , y , t ) is defined such that the ES is given by u ( x , y , t ) = e t sin ( π ( x 2 + y 2 ) ) .

Numerical errors for various values of M , N , and p are expressed in Tables 1 and 2, and the results obtained in the first column of Tables 1 and 2 demonstrate that by using Legendre-collocation spectral method, the solution of the problem becomes unstable and by applying the hybrid of regularization methods, the solution of the problem becomes stable. In addition, to compare these methods in Tables 1 and 2, can observe that MRSM is better than other methods. These results can show that with increasing values of M , N , and p , the errors decay exponentially. Clearly, all investigated hybrids of regularization and Legendre-collocation spectral methods give results with very close accuracy. The numerical results and exact solution are drawn in Figure 1, also the graph b in Figure 1 can see unstable method by using SM and the graph c in Figure 1 stable method by employing RSMs. From Figure 1, we obtain the answer to the precise and approximate solutions for M = 20 , N = 20 , and p = 20 . In Figure 2, we observe that with increasing time, the rate of error increases for the spectral method, and we use the MRSM to improve this problem for M = 20 , N = 20 , and p = 20 . In addition, we compare several regularization methods based on the Legendre-collocation spectral method with the same regularization parameter μ 1 = 1 × 1 0 − 1 in Tables 1 and 2, Figures 3 and 4. We can say that if the Gaussian integral accuracy is somewhat appropriate and good, we use the values of M and N to increase the accuracy of the solution of the differential-integral problem. In Figure 3, we show the different schemes and observe that the best method is MRSM. We review the best regularization parameter in Figure 5 for M = 20 , N = 20 , and p = 20 .

Table 1

The errors ‖ E ‖ ∞ obtained for Example (4.1) with RSMs and SM, when α = 1 and β = 1

M ( = N )	SM	TRSM	MRSM	ATRSM	RGRSM
6	1.3 × 1 0 1	0.03 × 1 0 − 6	1.83 × 1 0 − 10	1.95 × 1 0 − 9	0.45 × 1 0 − 4
10	1.45 × 1 0 2	2.65 × 1 0 − 7	2.78 × 1 0 − 9	1.66 × 1 0 − 10	0.45 × 1 0 − 6
14	2.03 × 1 0 4	1.78 × 1 0 − 8	3.01 × 1 0 − 11	2.87 × 1 0 − 11	0.58 × 1 0 − 7
18	1.07 × 1 0 6	3.98 × 1 0 − 9	1.79 × 1 0 − 13	3.96 × 1 0 − 12	0.98 × 1 0 − 8
20	2.25 × 1 0 7	2.14 × 1 0 − 10	1.19 × 1 0 − 14	2.70 × 1 0 − 13	0.05 × 1 0 − 9

Table 2

The errors ‖ E ‖ ∞ obtained for Example (4.1) with RSMs and SM, when α = 1 2 and β = 1

M ( = N )	SM	TRSM	MRSM	ATRSM	RGRSM
6	1.34 × 1 0 2	0.82 × 1 0 − 4	1.03 × 1 0 − 8	1.02 × 1 0 − 7	0.15 × 1 0 − 3
10	2.65 × 1 0 3	1.64 × 1 0 − 5	1.08 × 1 0 − 9	1.01 × 1 0 − 8	0.31 × 1 0 − 4
14	1.35 × 1 0 5	0.78 × 1 0 − 6	0.51 × 1 0 − 10	1.51 × 1 0 − 9	0.28 × 1 0 − 5
18	2.07 × 1 0 7	1.65 × 1 0 − 7	0.85 × 1 0 − 12	1.86 × 1 0 − 10	0.12 × 1 0 − 7
20	1.32 × 1 0 10	1.13 × 1 0 − 9	0.25 × 1 0 − 13	1.14 × 1 0 − 11	0.02 × 1 0 − 8

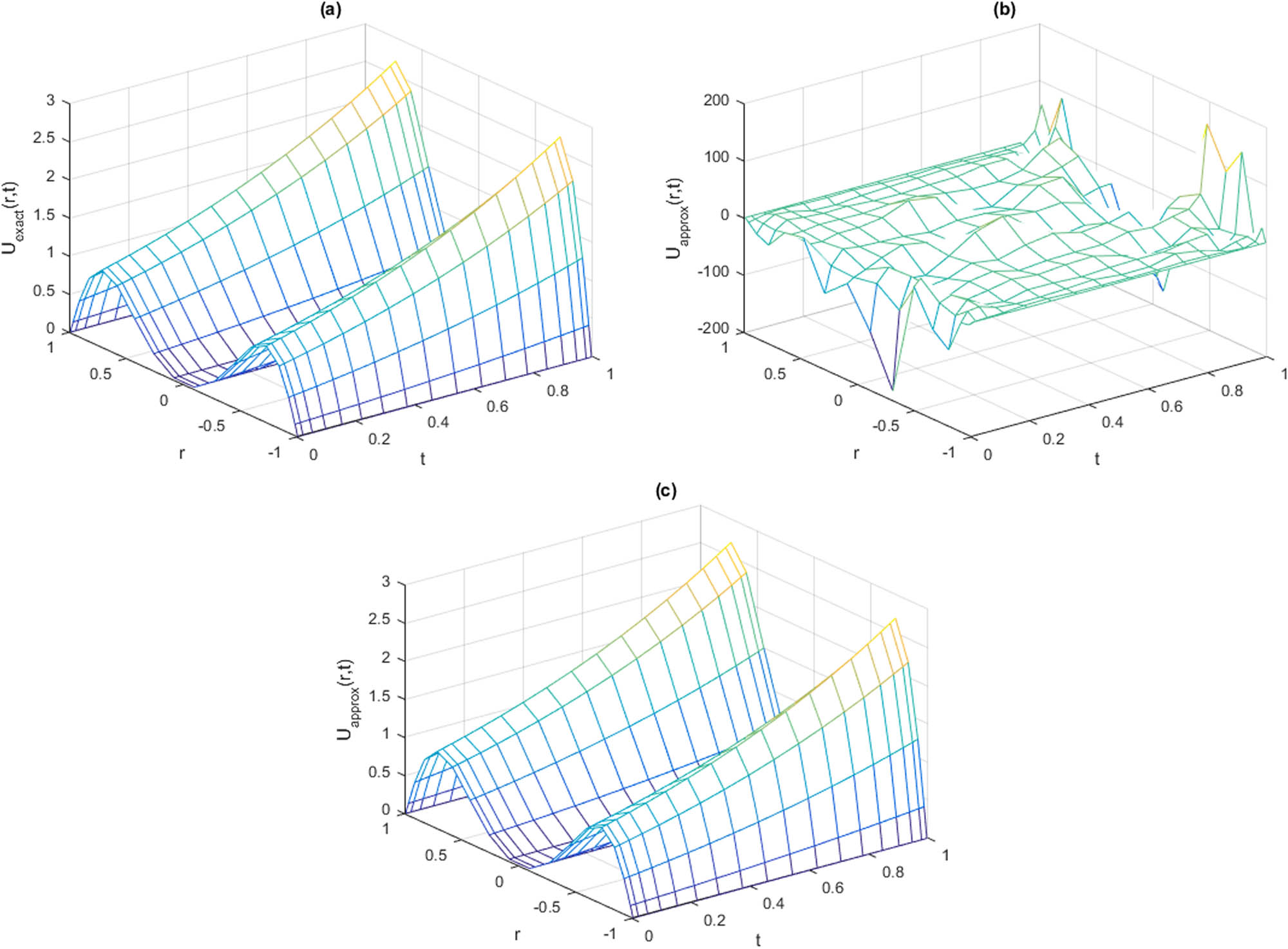
$Figure 1 The observations of Example 4.1 for N = M = 20 N=M=20 , (a) ES u ( x , y , t ) = e t sin ( π ( x 2 + y 2 ) ) u\left(x,y,t)={e}^{t}\sin \left(\pi \left({x}^{2}+{y}^{2})) ; (b) numerical solution with SM; and (c) numerical solution with MRSM for μ 1 = 1 × 1 0 − 1 {\mu }_{1}=1\times 1{0}^{-1} .$

Figure 1

The observations of Example 4.1 for N = M = 20 , (a) ES u ( x , y , t ) = e t sin ( π ( x 2 + y 2 ) ) ; (b) numerical solution with SM; and (c) numerical solution with MRSM for μ 1 = 1 × 1 0 − 1 .

$Figure 2 ES and behaviors of SM and MRSM for Example 4.1 for r ∈ [ − 1 , 1 ] r\in \left[-1,1] and M = 20 M=20 and various times t = 0.1 , 0.2 , 0.4 , 0.6 , 0.8 t=0.1,0.2,0.4,0.6,0.8 , and 0.9 0.9 with N = 20 N=20 , μ 1 = 1 × 1 0 − 1 {\mu }_{1}=1\times 1{0}^{-1} .$

Figure 2

ES and behaviors of SM and MRSM for Example 4.1 for r ∈ [ − 1 , 1 ] and M = 20 and various times t = 0.1 , 0.2 , 0.4 , 0.6 , 0.8 , and 0.9 with N = 20 , μ 1 = 1 × 1 0 − 1 .

$Figure 3 The absolute error of Example 4.1 by RSMs with t ∈ ( 0 , 1 ] t\in \left(0,1] and M = 4 , 6 , … , 20 M=4,6,\ldots ,20 , and r ∈ ( − 1 , 1 ) r\in \left(-1,1) and N = 4 , 6 , … , 20 N=4,6,\ldots ,20 at μ 1 = 0.1 {\mu }_{1}=0.1 with α = 1 \alpha =1 and β = 1 \beta =1 .$

Figure 3

The absolute error of Example 4.1 by RSMs with t ∈ ( 0 , 1 ] and M = 4 , 6 , … , 20 , and r ∈ ( − 1 , 1 ) and N = 4 , 6 , … , 20 at μ 1 = 0.1 with α = 1 and β = 1 .

$Figure 4 The absolute error of Example 4.1 by RSMs with t ∈ ( 0 , 1 ] t\in \left(0,1] and M = 4 , 6 , … , 20 M=4,6,\ldots ,20 , and r ∈ ( − 1 , 1 ) r\in \left(-1,1) and N = 4 , 6 , … , 20 N=4,6,\ldots ,20 at μ 1 = 0.1 {\mu }_{1}=0.1 with α = 1 2 \alpha =\frac{1}{2} and β = 1 \beta =1 .$

Figure 4

The absolute error of Example 4.1 by RSMs with t ∈ ( 0 , 1 ] and M = 4 , 6 , … , 20 , and r ∈ ( − 1 , 1 ) and N = 4 , 6 , … , 20 at μ 1 = 0.1 with α = 1 2 and β = 1 .

$Figure 5 The absolute error of Example 4.1 for regularization parameters when μ 1 ∈ [ 1 × 1 0 − 10 , 1 × 1 0 10 ] {\mu }_{1}\in \left[1\times 1{0}^{-10},1\times 1{0}^{10}] with M = 20 M=20 and N = 20 N=20 .$

Figure 5

The absolute error of Example 4.1 for regularization parameters when μ 1 ∈ [ 1 × 1 0 − 10 , 1 × 1 0 10 ] with M = 20 and N = 20 .

4.2 Unbounded domain

For this example, we study the nonlinear and linear HVIDEs, and by applying the algorithms presented in Section 3, the mapping parameter is set to Q = 1 . In unbounded domain is Ω = R 2 . The relative errors in the collocation points are given with L ∞ norm for different values of N and M .

Example 4.2

As the second example, consider the problem (3.32) with k ( x , y , t ) = e − ( x 2 + y 2 ) t and c ( x ) = x 2 + y 2 . The ES is u ( x , y , t ) = sin ( t ) 2 ( x 2 + y 2 ) , and the source function f ( x , y , t ) can be extracted from the analytical solution.

In Tables 3 and 4, the numerical results of maximum absolute errors for SM and the different RSMs are presented with μ 2 = 1 × 1 0 − 1 . In Figure 6, the numerical solutions and ES are plotted for M = 20 , N = 20 , and p = 20 . Again, we display in the first column of Tables 3 and 4 and the graph b of Figure 7 that increasing N and M leads to ill-posed SM method, and for improving it, we use the different hybrids of regularization methods. Similar to the previous examples by comparing the different RSMs in Tables 3 and 4, we observe that accuracy of MRSM with μ 2 = 1 × 1 0 − 1 is the best. Again, these results indicate the exponential rate of accuracy for the different RSMs. The graphs of the comparison of absolute errors with several regularization methods based on the Legendre-collocation spectral method with the same regularization parameter μ 2 = 1 × 1 0 − 1 are given in Figures 8 and 9. In addition, the absolute errors with the different regularization parameters are shown in Figure 10 for M = 20 , N = 20 , and p = 20 .

Table 3

The errors ‖ e ‖ ∞ obtained for Example (4.2) with RSMs and SM, when α = 1 2 and β = 1

M ( = N )	SM	TRSM	MRSM	ATRSM	RGRSM
6	09.28 × 1 0 2	0.03 × 1 0 − 4	1.15 × 1 0 − 8	5.02 × 1 0 − 7	0.40 × 1 0 − 2
10	08.71 × 1 0 3	3.68 × 1 0 − 5	1.58 × 1 0 − 9	7.23 × 1 0 − 6	1.68 × 1 0 − 3
14	10.28 × 1 0 5	1.92 × 1 0 − 7	3.59 × 1 0 − 10	4.22 × 1 0 − 8	1.19 × 1 0 − 5
18	09.52 × 1 0 6	2.68 × 1 0 − 8	2.09 × 1 0 − 11	5.13 × 1 0 − 9	2.84 × 1 0 − 6
20	11.35 × 1 0 7	1.75 × 1 0 − 9	1.52 × 1 0 − 13	6.96 × 1 0 − 11	2.25 × 1 0 − 7

Table 4

The errors ‖ e ‖ ∞ obtained for Example (4.2) with RSMs and SM, when α = 1 2 and β = 1

M ( = N )	SM	TRSM	MRSM	ATRSM	RGRSM
6	12.45 × 1 0 2	1.03 × 1 0 − 2	1.15 × 1 0 − 6	8.90 × 1 0 − 5	1.05 × 1 0 − 1
10	8.45 × 1 0 3	3.68 × 1 0 − 3	1.58 × 1 0 − 7	9.26 × 1 0 − 6	2.68 × 1 0 − 2
14	9.03 × 1 0 4	1.92 × 1 0 − 4	3.59 × 1 0 − 9	7.27 × 1 0 − 7	1.88 × 1 0 − 3
18	8.279 × 1 0 5	2.68 × 1 0 − 5	2.09 × 1 0 − 10	9.96 × 1 0 − 8	3.94 × 1 0 − 4
20	9.125 × 1 0 6	1.75 × 1 0 − 6	1.52 × 1 0 − 11	6.96 × 1 0 − 9	1.05 × 1 0 − 5

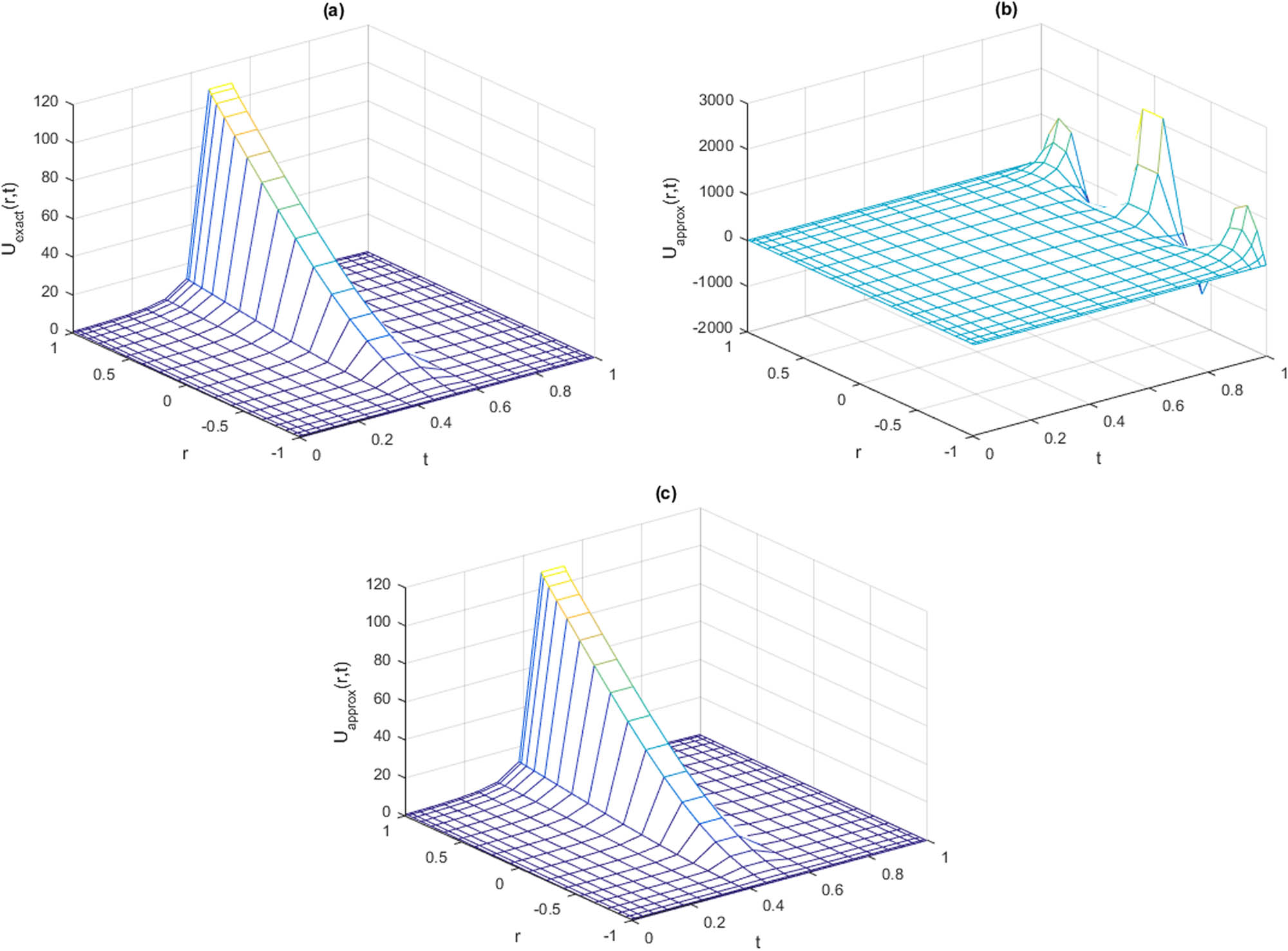
$Figure 6 The observations of Example 4.2 for N = M = 16 N=M=16 , (a) ES u ( x , y , t ) = sin ( t ) 2 ( x 2 + y 2 ) u\left(x,y,t)=\frac{{\sin \left(t)}^{2}}{\left({x}^{2}+{y}^{2})} ; (b) numerical solution with SM; and (c) numerical solution with MRSM for μ 2 = 1 × 1 0 − 1 {\mu }_{2}=1\times 1{0}^{-1} .$

Figure 6

The observations of Example 4.2 for N = M = 16 , (a) ES u ( x , y , t ) = sin ( t ) 2 ( x 2 + y 2 ) ; (b) numerical solution with SM; and (c) numerical solution with MRSM for μ 2 = 1 × 1 0 − 1 .

$Figure 7 ES and behaviors of SM and MRSM for Example 4.2 for r ∈ [ − 1 , 1 ] r\in \left[-1,1] with M = 20 M=20 and various times t = 0.1 , 0.2 , 0.4 , 0.6 , 0.8 t=0.1,0.2,0.4,0.6,0.8 and 0.09 0.09 with N = 20 N=20 , μ 2 = 1 × 1 0 − 1 {\mu }_{2}=1\times 1{0}^{-1} .$

Figure 7

ES and behaviors of SM and MRSM for Example 4.2 for r ∈ [ − 1 , 1 ] with M = 20 and various times t = 0.1 , 0.2 , 0.4 , 0.6 , 0.8 and 0.09 with N = 20 , μ 2 = 1 × 1 0 − 1 .

$Figure 8 The absolute error of Example 4.2 by RSMs with t ∈ ( 0 , 1 ] t\in \left(0,1] and M = 4 , 6 , … , 20 M=4,6,\ldots ,20 , and r ∈ [ − 1 , 1 ] r\in \left[-1,1] and N = 4 , 6 , … , 20 N=4,6,\ldots ,20 at μ 2 = 1 × 1 0 − 1 {\mu }_{2}=1\times 1{0}^{-1} with α = 1 \alpha =1 and β = 1 \beta =1 .$

Figure 8

The absolute error of Example 4.2 by RSMs with t ∈ ( 0 , 1 ] and M = 4 , 6 , … , 20 , and r ∈ [ − 1 , 1 ] and N = 4 , 6 , … , 20 at μ 2 = 1 × 1 0 − 1 with α = 1 and β = 1 .

$Figure 9 The absolute error of Example 4.2 by RSMs with t ∈ ( 0 , 1 ] t\in \left(0,1] and M = 4 , 6 , … , 20 M=4,6,\ldots ,20 , and r ∈ [ − 1 , 1 ] r\in \left[-1,1] and N = 4 , 6 , … , 20 N=4,6,\ldots ,20 at μ 2 = 1 × 1 0 − 1 {\mu }_{2}=1\times 1{0}^{-1} with α = 1 2 \alpha =\frac{1}{2} and β = 1 \beta =1 .$

Figure 9

The absolute error of Example 4.2 by RSMs with t ∈ ( 0 , 1 ] and M = 4 , 6 , … , 20 , and r ∈ [ − 1 , 1 ] and N = 4 , 6 , … , 20 at μ 2 = 1 × 1 0 − 1 with α = 1 2 and β = 1 .

$Figure 10 The absolute error of Example 4.2 for regularization parameters with μ 2 ∈ [ 1 × 1 0 − 10 , 1 × 1 0 + 10 ] {\mu }_{2}\in \left[1\times 1{0}^{-10},1\times 1{0}^{+10}] at t ∈ ( 0 , 1 ] t\in \left(0,1] with M = 20 M=20 and N = 20 N=20 .$

Figure 10

The absolute error of Example 4.2 for regularization parameters with μ 2 ∈ [ 1 × 1 0 − 10 , 1 × 1 0 + 10 ] at t ∈ ( 0 , 1 ] with M = 20 and N = 20 .

5 Conclusion

In this article, we proposed a hybrid of numerical schemes for high-dimensional HVIDEs based on a Legendre-collocation spectral method. We consider the problem on a bounded and unbounded spatial domains. For convenience, first we restate the original second-order Volterra integrodifferential equation as three simple integral equations of the second kind and used the Legendre-collocation spectral method for each one, which leads to conversion of the problem to solving the linear and nonlinear algebraic systems. For solving the problem on an unbounded domain, we use the algebraic mapping to transfer the equation in a bounded domain and then apply the same approach for the bounded case. By using the Legendre-collocation spectral methods, nonlinear and linear systems of equations of the form (1.1) and (3.32) with a matrix of ill-determined rank are obtained when discretizing linear ill-posed problems. The most important contribution of this work is that we are able to apply the regularization method to solve an ill-posed linear systems of algebraic equation. The numerical examples illustrate that using the regularization methods can improve the quality of the computed approximate solution. In addition, we can solve the following nonlinear equation by applying the proposed method. Moreover, point-wise error calculation is discussed in this article.

For studying the computational complexity of the proposed methods due to the scope of the discussion (see ref. [45] for details), this important issue needs to be presented in another article. In addition, for studying the error bounds, finding space of solutions with singular and weakly singular kernels and regularity of the solutions, we need to introduce special spaces based on functional analysis. Therefore, these discussions are left to the future.

Acknowledgments

The authors would like to thank the three anonymous referees for very helpful comments that have led to an improvement of the article.

Funding information: The authors state no funding involved.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Wei Y, Chen Y. Legendre spectral collocation method for neutral and high-order Volterra integrodifferential equation. Appl Numer Math. 2014;81(4):15–29. 10.1016/j.apnum.2014.02.012Search in Google Scholar

[2] Vlasov VV, Rautian NA. Spectral analysis of hyperbolic Volterra integrodifferential equations. Doklady Math. 2015;92(2):590–3. 10.1134/S1064562415050324Search in Google Scholar

[3] Belhannache F, Algharabli MM, Messaoudi SA. Asymptotic stability for a viscoelastic equation with nonlinear damping and very general type of relaxation functions. J Dynam Control Syst. 2020;26(1):45–67. 10.1007/s10883-019-9429-zSearch in Google Scholar

[4] Dafermos CM. An abstract Volterra equation with applications to linear viscoelasticity. J Diff Equ. 1970;7(3):554–69. 10.1016/0022-0396(70)90101-4Search in Google Scholar

[5] Renardy M, Hrusa WJ, Nohel JA. Mathematical Problems in viscoelasticity. Essex, UK: Longman Science and Technology; 1987;35. Search in Google Scholar

[6] Rostamy D, Mirzaei F. A class of developed schemes for parabolic integrodifferential equations. Int J Comput Math. 2021;98(12):2482–503. 10.1080/00207160.2021.1901278Search in Google Scholar

[7] Saedpanah F. Optimal order finite element approximation for a hyperbolic integro-differential equation. Bull Iran Math Soc. 2012;38(2):447–59. Search in Google Scholar

[8] Dix JG, Torrejon RM. A quasilinear integrodifferential equation of hyperbolic type. Diff Int Equ. 1993;6(2):431–47. 10.57262/die/1370870199Search in Google Scholar

[9] Torrejon R, Yong J. On a quasilinear wave equation with memory. Non Anal Theory Meth Appl. 1991;16:61–78. 10.1016/0362-546X(91)90131-JSearch in Google Scholar

[10] Yanik E, Fairweather G. Finite element methods for parabolic and hyperbolic partial integrodifferential equations. Non Anal Theory Meth Appl. 1988;12(8):785–809. 10.1016/0362-546X(88)90039-9Search in Google Scholar

[11] Hrusa WJ, Renardy M. On wave propagation in linear viscoelasticity. Quart Appl Math. 1985;43(2):237–54. 10.21236/ADA144739Search in Google Scholar

[12] Choi UJ, Macamy RC. Fractional order Volterra equations with applications to elasticity. J Math Anal Appl. 1989;139(2):448–64. 10.1016/0022-247X(89)90120-0Search in Google Scholar

[13] Lin Y, Thomeae V, Wahlbin LB. Ritz-Volterra projections to finite-element spaces and application to integrodifferential and related equations. SIAM J Numer Anal. 1991;28(4):1047–70. 10.1137/0728056Search in Google Scholar

[14] Chung SK, Park MG. Spectral analysis for hyperbolic integrodifferential equations with a weakly singular kernel. J Ksiam. 1998;2(2):31–40. Search in Google Scholar

[15] H. Engler. Weak solutions of a class of quasilinear hyperbolic integrodifferential equations describing viscoelastic materials. Arch Rat Mech Anal. 1991;113(1):1–38. 10.1007/BF00380814Search in Google Scholar

[16] Karaa S, Pani A, Yadav S. A priori hp-estimates for discontinuous Galerkin approximations to linear hyperbolic integrodifferential equations. Appl Numer Math. 2015;96:1–23. 10.1016/j.apnum.2015.04.006Search in Google Scholar

[17] Gan XT, Yin JF. Symmetric finite volume element approximations of second-order linear hyperbolic integrodifferential equations. Comput Math Appl. 2015;70(10):2589–600. 10.1016/j.camwa.2015.09.019Search in Google Scholar

[18] Merad A, Martin-Vaquero J. A Galerkin method for two-dimensional hyperbolic integrodifferential equation with purely integral conditions. Appl Math Comput. 2016;291:386–94. 10.1016/j.amc.2016.07.003Search in Google Scholar

[19] Pani AK, Thomeae V, Wahlbin LB. Numerical methods for hyperbolic and parabolic integro-differential equations. J Int Equ Appl. 1992;4(4):533–84. 10.1216/jiea/1181075713Search in Google Scholar

[20] Shi X, Wei Y, Huang F. Spectral collocation methods for nonlinear weakly singular Volterra integrodifferential equations. Numer Meth Partial Diff Equ. 2019;35(2):576–96. 10.1002/num.22314Search in Google Scholar

[21] Ezz-Eldien SS, Doha EH, Fast and precise spectral method for solving pantograph type Volterra integrodifferential equations. Numer Algor. 2019;81(2):57–77. 10.1007/s11075-018-0535-xSearch in Google Scholar

[22] Faheem M, Raza A, Khan A. Collocation methods based on Gegenbauer and Bernoulli wavelets for solving neutral delay differential equations. Math Comput Simul. 2021;180:72–92. 10.1016/j.matcom.2020.08.018Search in Google Scholar

[23] Sadri K, Hosseini K, Baleanu D, Ahmadian A, Salahshour S. Bivariate Chebyshev polynomials of the fifth kind for variable-order time-fractional partial integrodifferential equations with weakly singular kernel. Adv Diff Equ. 2021;348(1):1–26. 10.1186/s13662-021-03507-5Search in Google Scholar

[24] Sadri K, Hosseini K, Baleanu D, Salahshour S, Park C. Designing a matrix collocation method for fractional delay integrodifferential equations with weakly singular kernels based on vieta-Fibonacci polynomials. Fractal Fract. 2021;6(1):2. 10.3390/fractalfract6010002Search in Google Scholar

[25] Sadri K, Hosseini K, Mirzazadeh M, Ahmadian A, Salahshour S, Singh J. Bivariate Jacobi polynomials for solving Volterra partial integrodifferential equations with the weakly singular kernel. Math Meth Appl Sci. 2021. https://doi.org/10.1002/mma.7662. 10.1002/mma.7662Search in Google Scholar

[26] Wu N, Zheng W, Gao W. Symmetric spectral collocation method for a kind of nonlinear Volterra integral equation. Symmetry. 2022;14(6):1091. 10.3390/sym14061091Search in Google Scholar

[27] Tang J, Mab H. A Legendre spectral method in time for first-order hyperbolic equations. Appl Numer Math. 2007;57(1):1–11. 10.1016/j.apnum.2005.11.009Search in Google Scholar

[28] Tang T, Xu X, Cheng J. On spectral methods for Volterra type integral equations and the convergence analysis. J Comput Math. 2008;26(6):825–37. Search in Google Scholar

[29] Jiang Y. On spectral methods for Volterra-type integrodifferential equations. J Comput App Math. 2009;230(2):333–40. 10.1016/j.cam.2008.12.001Search in Google Scholar

[30] Jiang Y, Ma J. Spectral collocation methods for Volterra-integrodifferential equations with noncompact kernels. J Comput Appl Math. 2013;244(1):115–24. 10.1016/j.cam.2012.10.033Search in Google Scholar

[31] Davis PJ. Interpolation and approximation. Mineola, New York: Dover Publications; 1975. Search in Google Scholar

[32] Henry D. Geometric theory of semilinear parabolic equations. Berlin, Heidelberg: Springer-Verlag; 1989. Search in Google Scholar

[33] Sahu PK, SahaRay S. Legendre spectral collocation method for Fredholm integrodifferential-difference equation with variable coefficients and mixed conditions. Appl Math Comput. 2015;268:575–80. 10.1016/j.amc.2015.06.118Search in Google Scholar

[34] Adewumi AO, Akindeinde SO, Lebelo RS. Sumudu Lagrange-spectral methods for solving system of linear and nonlinear Volterra integrodifferential equations. Appl Numer Math. 2021;169:146–63. 10.1016/j.apnum.2021.06.012Search in Google Scholar

[35] Wei Y, Chen Y. Legendre spectral collocation method for Volterra-Hammerstein integral equation of the second Kind. Acta Math Sci. 2017;37(4):1105–14. 10.1016/S0252-9602(17)30060-7Search in Google Scholar

[36] Qu CK, Wong R. Szegö’s conjecture on Lebesgue constants for Legendre series. Pacific J Math. 1988;135(1):157–88. 10.1142/9789814656054_0021Search in Google Scholar

[37] Costa B, Donb WS. On the computation of high order pseudospectral derivatives. Appl Numer Math. 2000;33(1–4):151–9. 10.1016/S0168-9274(99)00078-1Search in Google Scholar

[38] Shen J, Tang T, Wang L. Spectral methods: algorithms, analysis and applications. Berlin, Heidelberg: Springer; 2011.10.1007/978-3-540-71041-7Search in Google Scholar

[39] Engl HW, Hanke M, Neubauer A. Regularization of inverse problems. Dordrecht: Springer; 1996. 10.1007/978-94-009-1740-8Search in Google Scholar

[40] Lewis B, Reichel L. Arnoldi-Tikhonov regularization methods. J Comput Appl Math. 2009;226(1):92–102. 10.1016/j.cam.2008.05.003Search in Google Scholar

[41] Calvetti D, Lewis B, Reichel L. On the choice of subspace for iterative method for linear discrete ill-posed problems. Int J Appl Math Comput Sci. 2001;11(5):1069–92. Search in Google Scholar

[42] Hansen PC, Jensen TK. Smoothing norm preconditioning for regularizing minimum residual methods. SIAM J Matrix Anal Appl. 2006;29(1):1–14. 10.1137/050628453Search in Google Scholar

[43] Fletcher R. Practical optimization methods. Unconstrained optimization. Chichester: Wiley; 1980. Search in Google Scholar

[44] Hansen PC. Regularization tools: A Matlab package for analysis and solution of discrete ill-posed problems. Numer Algorithms. 1994;6(1):1–35. Software is available in Netlib at the web site http://www.netlib.org. 10.1007/BF02149761Search in Google Scholar

[45] Matache AM, Schwab C, Wihler TP. Linear complexity solution of parabolic integrodifferential equations. Numer Math. 2006;104(1):69–102. 10.1007/s00211-006-0006-5Search in Google Scholar

Received: 2022-04-23

Revised: 2022-08-09

Accepted: 2022-08-28

Published Online: 2023-02-08

This work is licensed under the Creative Commons Attribution 4.0 International License.

The regularization of spectral methods for hyperbolic Volterra integrodifferential equations with fractional power elliptic operator

Abstract

1 Introduction

2 Legendre and Lagrange polynomials and their properties

3 Implementation of Legendre-collocation spectral method

3.1 Change of variables for two-dimensional of Eq. (1.1)

3.2 Bounded domain

3.3 Unbounded domain

3.4 Regularization formula for Eqs (3.30) and (3.47)

4 Applications and numerical results

4.1 Bounded domain

Example 4.1

4.2 Unbounded domain

Example 4.2

5 Conclusion

Acknowledgments

References

Journal and Issue

Articles in the same Issue