Covariance Matrix

Last Updated : 02 Sep, 2024
Comments
Improve
Suggest changes
Like Article
Like
Save
Share
Report
News Follow

Covariance Matrix is a type of matrix used to describe the covariance values between two items in a random vector. It is also known as the variance-covariance matrix because the variance of each element is represented along the matrix’s major diagonal and the covariance is represented among the non-diagonal elements.

It’s particularly important in fields like data science, machine learning, and finance, where understanding relationships between multiple variables is crucial and comes in handy when it comes to stochastic modeling and principal component analysis.

In this article, we will discuss various things related to the Covariance Matrix such as its definition, example, and formula.

Table of Content

What is Covariance Matrix?

The variance-covariance matrix is a square matrix with diagonal elements that represent the variance and the non-diagonal components that express covariance. The covariance of a variable can take any real value- positive, negative, or zero. A positive covariance suggests that the two variables have a positive relationship, whereas a negative covariance indicates that they do not. If two elements do not vary together, they have a zero covariance.

Learn More, Diagonal Matrix

Covariance Matrix Example 

Let’s say there are 2 data sets X = [10, 5] and Y = [3, 9]. The variance of Set X = 6.5 and the variance of set Y = 9. The covariance between both variables is -15. The covariance matrix is as follows:

\begin{bmatrix} Variance~of~Set~X & Covariance~of~Both~Sets\\ Covariance~of~Both~Sets& Variance~of~Set~Y \end{bmatrix}=\begin{bmatrix} 6.5 & -15\\ -15& 9 \end{bmatrix}

Covariance Matrix Formula

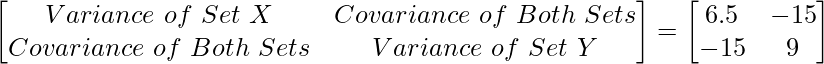
The general form of a covariance matrix is given as follows:

Covariance Matrix

Where,

  • Sample Variance: var(x1) = \frac{\sum_{1}^{n}\left ( x_{i} -\overline{x}\right )^{2} }{n-1}
  • Sample Covarinace: cov(x1, y1) = \frac{\sum_{1}^{n}\left (x_{i} -\overline{x}\right )\left(y_{i}-\overline{y}\right)}{n-1}
  • Population Variance: var(xn) = \frac{\sum_{1}^{n}\left ( x_{i} -\mu\right )^{2} }{n}
  • Population Covariance: cov(xn, yn) = \frac{\sum_{1}^{n}\left ( x_{i} -\mu_{x}\right )\left ( y_{i}-\mu_{y} \right ) }{n}

Here, μ is Mean of Population

\overline x is Mean of Sample

n is Number of Observation

xi is the Observation in Dataset x

Let’s see the format of Covariance Matrix of 2 ⨯ 2 and 3 ⨯ 3.

2 ⨯ 2 Covariance Matrix

We know that in a 2 ⨯ 2 matrix there are two rows and two columns. Hence, the 2 ⨯ 2 Covariance Matrix can be expressed as \begin{bmatrix}\mathrm{var(x)}& \mathrm{cov(x,y)} \\\mathrm{cov(x,y)} &\mathrm{var(y)}\end{bmatrix}

3 ⨯ 3 Covariance Matrix

In a 3⨯3 Matrix there are 3 rows and 3 columns. We know that in a Covariance Matrix the diagonal elements are variance and non-diagonal elements are covariance. Hence, a 3⨯3 Covariance Matrix can be given as \begin{bmatrix}\mathrm{var(x)}&\mathrm{cov(x,y)} &\mathrm{cov(x,z)} \\\mathrm{cov(x,y)} &\mathrm{var(y)} &\mathrm{cov(y,z)} \\\mathrm{cov(x,z)} &\mathrm{cov(y,z)} &\mathrm{var(z)} \\\end{bmatrix}

How to Find Covariance Matrix?

The dimensions of a covariance matrix are determined by the number of variables in a given data set. If there are only two variables in a set, then the covariance matrix would have two rows and two columns. Similarly, if a data set has three variables, then its covariance matrix would have three rows and three columns. 

The data pertains to marks scored by Anna, Caroline, and Laura in Psychology and History. Make a covariance matrix.

StudentPsychology(X)History(Y)
Anna8070
Caroline6320
Laura10050

The following steps have to be followed:

Step 1: Find the mean of variable X. Sum up all the observations in variable X and divide the sum obtained with the number of terms. Thus, (80 + 63 + 100)/3 = 81.

Step 2: Subtract the mean from all observations. (80 – 81), (63 – 81), (100 – 81).

Step 3: Take the squares of the differences obtained above and then add them up. Thus, (80 – 81)2 + (63 – 81)2 + (100 – 81)2.

Step 4: Find the variance of X by dividing the value obtained in Step 3 by 1 less than the total number of observations. var(X) = [(80 – 81)2 + (63 – 81)2 + (100 – 81)2] / (3 – 1) = 343.

Step 5: Similarly, repeat steps 1 to 4 to calculate the variance of Y. Var(Y) = 633.333

Step 6: Choose a pair of variables.

Step 7: Subtract the mean of the first variable (X) from all observations; (80 – 81), (63 – 81), (100 – 81).

Step 8: Repeat the same for variable Y; (70 – 47), (20 – 47), (50 – 47).

Step 9: Multiply the corresponding terms: (80 – 81)(70 – 47), (63 – 81)(20 – 47), (100 – 81)(50 – 47).

Step 10: Find the covariance by adding these values and dividing them by (n – 1). Cov(X, Y) = [(80 – 81)(70 – 47) + (63 – 81)(20 – 47) + (100 – 81)(50 – 47)]/(3-1) = 260.

Step 11: Use the general formula for the covariance matrix to arrange the terms. The matrix becomes: \begin{bmatrix} 343 & 260\\ 260& 633.333 \end{bmatrix}

Properties of Covariance Matrix

The Properties of Covariance Matrix are mentioned below:

  • A covariance matrix is always square, implying that the number of rows in a covariance matrix is always equal to the number of columns in it.
  • A covariance matrix is always symmetric, implying that the transpose of a covariance matrix is always equal to the original matrix.
  • A covariance matrix is always positive and semi-definite.
  • The eigenvalues of a covariance matrix are always real and non-negative.

Read More,

Solved Examples on Covariance Matrix

Example 1: The marks scored by 3 students in Physics and Biology are given below:

StudentPhysics(X)Biology(Y)
A9280
B6030
C10070

Calculate Covariance Matrix from the above data.

Solution:

Sample covariance matrix is given by \frac{\sum_{1}^{n}\left ( x_{i} -\overline{x}\right )^{2} }{n-1} .

Here, μx = 84, n = 3

var(x) = [(92 – 84)2 + (60 – 84)2 + (100 – 84)2] / (3 – 1) = 448

Also, μy = 60, n = 3

var(y) = [(80 – 60)2 + (30 – 60)2 + (70 – 60)2] / (3 – 1) = 700

Now, cov(x, y) = cov(y, x) = [(92 – 84)(80 – 60) + (60 – 84)(30 – 60) + (100 – 84)(70 – 60)] / (3 – 1) = 520.

The population covariance matrix is given as: \begin{bmatrix} 448 & 520\\ 520& 700 \end{bmatrix}

Example 2. Prepare the population covariance matrix from the following table:

AgeNumber of People
2968
2660
3058
3540

Solution:

Population variance is given by \frac{\sum_{1}^{n}\left ( x_{i} -\mu\right )^{2} }{n} .

Here, μx = 56.5, n = 4

var(x) = [(68 – 56.5)2 + (60 – 56.5)2 + (58 – 56.5)2 + (40 – 56.5)2 ] / 4 = 104.75

Also, μy = 30, n = 4

var(y) = [(29 – 30)2 + (26 – 30)2 + (30 – 30)2 + (35 – 30)2] / 4 = 10. 5

Now, cov(x, y) = \frac{\sum_{1}^{4}\left ( x_{i} -\mu_{x}\right )\left ( y_{i}-\mu_{y} \right ) }{4}

cov(x, y) = -27

The population covariance matrix is given as: \begin{bmatrix} 104.7 &-27 \\ -27& 10.5 \end{bmatrix}

Example 3. Interpret the following covariance matrix:

\begin{bmatrix} & X & Y & Z\\ X & 60 & 32 & -4\\ Y & 32 & 30 & 0\\ Z & -4 & 0 & 80 \end{bmatrix}

Solution:

  1. The diagonal elements 60, 30, and 80 indicate the variance in data sets X, Y, and Z respectively. Y shows the lowest variance whereas Z displays the highest variance.
  2. The covariance for X and Y is 32. As this is a positive number it means that when X increases (or decreases) Y also increases (or decreases)
  3. The covariance for X and Z is -4. As it is a negative number it implies that when X increases Z decreases and vice-versa.
  4. The covariance for Y and Z is 0. This means that there is no predictable relationship between the two data sets.

Example 4. Find the sample covariance matrix for the following data:

XYZ
7510.545
6512.865
227.374
152.176
189.256

Solution:

Sample covariance matrix is given by \frac{\sum_{1}^{n}\left ( x_{i} -\overline{x}\right )^{2} }{n-1} .

n = 5,

  • μx = 22.4, var(X) = 321.2 / (5 – 1) = 80.3
  • μy = 12.58, var(Y) = 132.148 / 4 = 33.037
  • μz = 64, var(Z) = 570 / 4 = 142.5

Now, cov(X, Y) = \frac{\sum_{1}^{5}\left ( x_{i} -22.4\right )\left ( y_{i}-12.58\right ) }{5-1} = -11.76

⇒ cov(X, Z) = \frac{\sum_{1}^{5}\left ( x_{i} -22.4\right )\left ( z_{i}-64 \right ) }{5-1} = 34.97

⇒ cov(Y, Z) = \frac{\sum_{1}^{5}\left ( y_{i} -12.58\right )\left ( z_{i}-64 \right ) }{5-1} = -40.87

The covariance matrix is  given as:

\begin{bmatrix} 80.3 & -13.865 &14.25 \\ -13.865 & 33.037 & -39.5250\\ 14.25 & -39.5250 & 142.5 \end{bmatrix}

Practice Problems on Covariance Matrix

Problem 1: Given two sets of data points: X = [2, 4, 6, 8, 10] and Y = [1, 3, 5, 7, 9], calculate the covariance between X and Y.

Problem 2: Calculate the covariance matrix for the following dataset:

X1

X2

X3

4

2

0

4

5

6

8

10

12

12`

9

6

Problem 3: Given the covariance matrix:

\Sigma = \begin{bmatrix} 4 & -2 & 0 \\ -2 & 3 & 1 \\ 0 & 1 & 5 \\ \end{bmatrix}

Identify the variances and covariances between the variables.

FAQs on Covariance Matrix

Define Covariance Matrix

A covariance matrix is a type of matrix used to describe the covariance values between two items in a random vector.

What is the Formula for Covariance Matrix?

The Formula for Covariance Matrix is given as

\left[\begin{array}{ccc} \operatorname{Var}\left(x_1\right) & \ldots \ldots & \operatorname{Cov}\left(x_n, x_1\right) \\ \vdots & \ldots & \vdots \\ \vdots & \ldots & \vdots \\ \operatorname{Cov}\left(x_n, x_1\right) & \ldots \ldots & \operatorname{Var}\left(x_n\right) \end{array}\right]

Where, Sample Variance: var(x1) = \frac{\sum_{1}^{n}\left ( x_{i} -\overline{x}\right )^{2} }{n-1}

  • Sample Covarinace: cov(x1, y1) = \frac{\sum_{1}^{n}\left (x_{i} -\overline{x}\right )\left(y_{i}-\overline{y}\right)}{n-1}
  • Population Variance: var(xn) = \frac{\sum_{1}^{n}\left ( x_{i} -\mu\right )^{2} }{n}
  • Population Covariance: cov(xn, yn) = \frac{\sum_{1}^{n}\left ( x_{i} -\mu_{x}\right )\left ( y_{i}-\mu_{y} \right ) }{n}

What is the General Form of a 3 ⨯ 3 Covariance Matrix?

The general form of a 3 ⨯ 3 covariance matrix is given as follows:

\begin{bmatrix}\mathrm{var(x)}&\mathrm{cov(x,y)} &\mathrm{cov(x,z)} \\\mathrm{cov(x,y)} &\mathrm{var(y)} &\mathrm{cov(y,z)} \\\mathrm{cov(x,z)} &\mathrm{cov(y,z)} &\mathrm{var(z)} \\\end{bmatrix}

What are the Properties of Covariance Matrix?

Covariance Matrix is a square matrix and is also symmetric in nature i.e. the transpose of the original matrix gives the original matrix itself

What are the sectors where Covariance Matrix can be used?

Covariance Matrix is used in the field of Mathematics, Machine Learning, Finance and Economics. Covariance Matrix is used in Cholskey Decomposition to perfom Monte Carlo Simulation which is used to create Mathematical Models.



P
prabhjotkushparmar
News
Improve
Previous Article
DeMoivre's Theorem
Next Article
Determinant of Matrix with Solved Examples

Similar Reads

Can Covariance be Negative
Statistics is an important mathematical concept that helps us to understand our quantitative data. We mainly use either Descriptive Statistics or Inferential Statistics. Descriptive Statistics is mainly used to analyze past data or trends. Inferential Statistics is the second category that is used for predictions for the population based on a rando
5 min read
Covariance and Correlation
Covariance and correlation are the two key concepts in Statistics that help us analyze the relationship between two variables. Covariance measures how two variables change together, indicating whether they move in the same or opposite directions. However, its magnitude can be difficult to interpret because it's not standardized. Correlation, refine
6 min read
How to find the Diagonal of a Matrix?
British Mathematician Arthur Cayley was the first person to develop the algebraic aspect of the matrix. After that, Psychiat Heisenberg used matrices as a tool to explain his famous Quantum principle. The study of matrices originated while solving different types of simple and complex linear problems, which is cumbersome to solve without matrices.
6 min read
Idempotent Matrix
A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. A matrix is said to be an "m by n" matrix when it has "m" rows and "n" columns and is written as an "m × n" matrix. For example, a matrix of order "5 × 6" has five rows and six
6 min read
Involutory Matrix
Involutory Matrix is defined as the matrix that follows self inverse function i.e. the inverse of the Involutory matrix is the matrix itself. A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. A matrix is said to be an "m by n"
6 min read
Cell-to-Matrix Interaction
The human body might seem like a strange structure. There are a lot of organs & components present in the human body. But those are not the complete background of the human body. There are several tiny elements are present in the body that helps to provide a body structure. There are millions of millions such elements present in each body. All
11 min read
Extracellular Matrix Proteins
The extracellular matrix can be understood as a suspension of macromolecules that aids in the maintenance of a complete organ as well as local tissue growth. All of these chemicals were secreted by nearby cells. The proteins will undergo scaffolding after being secreted. The transitory structures that form between individual proteins to create more
8 min read
Inverse of 2x2 Matrix
Inverse of a 2 × 2 Matrix is a matrix that, when multiplied by the original matrix, results in the identity matrix. It is an important concept in linear algebra and is used to find the solution of a system of linear equations. There are various methods of finding the inverse of the matrix which we will discuss further in the article. This article o
12 min read
Adjoint of a Matrix
Knowledge of matrices is necessary for various branches of mathematics. Matrices are one of the most powerful tools in mathematics. From matrices there come Determinants, Now we see one of the properties of the Determinant in this article. In this article, we see how to find the Adjoint of a Matrix. To know about the Adjoint of a Matrix we have to
13 min read
Determinant of 3×3 Matrix
Determinant is a fundamental concept in linear algebra used to find a single scalar value for the given matrix. This article will explain what is a 3 × 3 Matrix and how to calculate the Determinant of a 3 × 3 Matrix step by step, as well as, its applications. Whether you are a student learning linear algebra or an enthusiast seeking a deeper unders
13 min read
Inverse of 3x3 Matrix
Inverse of a 3 × 3 matrix is a matrix which when multiplied by the original Matrix gives the identity matrix as the product. Inverse of a Matrix is a fundamental aspect of linear algebra. This process plays a crucial role in solving systems of linear equations and various mathematical applications. To calculate the inverse, it is required to calcul
11 min read
Column Matrix
A rectangular array of numbers that are arranged in rows and columns is known as a "matrix." The size of a matrix can be determined by the number of rows and columns in it. If a matrix has "m" rows and "n" columns, then it is said to be an "m by n" matrix and is written as an "m × n" matrix. For example, if a matrix has five rows and three columns,
7 min read
Row Matrix
Row Matrix: A rectangular array of numbers that are arranged in rows and columns is known as a "matrix." The size of a matrix can be determined by the number of rows and columns in it. If a matrix has "m" rows and "n" columns, then it is said to be an "m by n" matrix and is written as an "m × n" matrix. In mathematics, a row matrix is a matrix char
7 min read
Identity Matrix
Identity Matrix is a square matrix whose all diagonal elements are equal to 1 and rest all elements are zero. Identity Matrix is also known as Unit Matrix. In simple terms, all diagonal elements are equal to 1 and rest are zero. The main condition for Identity matrix is that it should be a square matrix i.e. the no of rows should be equal to zero.
6 min read
Transformation Matrix
Transformation matrices are the core notions in linear algebra and these can help make advancements in many areas including computer graphics, image processing, and so on. Zero vectors and the corresponding unit vectors provide a compact and generalized manner of applying transformations to vectors or points in a coordinate system. In this article,
10 min read
Determinant of 4x4 Matrix | Examples and How to Find
Determinant of 4x4 Matrix: Determinant of a Matrix is a fundamental concept in linear algebra, essential for deriving a single scalar value from the matrix. 4x4 is a square matrix with 4 rows and 4 columns whose determinant can be found by a formula which we will discuss. This article will explore the definition of a 4 × 4 matrix and guide through
15+ min read
Methods to Find Inverse of a Matrix
Methods to find the inverse of a matrix involve the inverse of a matrix formula and by elementary operations. The inverse of matrix A is represented as A-1 which when multiplied by matrix A gives an identity matrix. In this article, we will explore different methods to find the inverse of a matrix in detail along with the inverse of matrix definiti
10 min read
Orthogonal Matrix
A Matrix is an Orthogonal Matrix when the product of a matrix and its transpose gives an identity value. An orthogonal matrix is a square matrix where transpose of Square Matrix is also the inverse of Square Matrix. Orthogonal Matrix in Linear Algebra is a type of matrices in which the transpose of matrix is equal to the inverse of that matrix. As
11 min read
Nilpotent Matrix
Nilpotent Matrices are special types of square matrices, they are special because the product of a Nilpotent Matrix with itself is equal to a null matrix. Let's take a square matrix A of order n × n it is considered a nilpotent matrix if Ak = 0. Here k is always less than equal to n.  In this article, we will learn about the Nilpotent Matrix in det
7 min read
Methods to Find Rank of a Matrix
To find the rank of a matrix find the highest order of the non-zero minor within the matrix. Rank of a matrix in the number that represents the number of non-zeros rows or columns in the matrix. If the rank of the matrix is r then the matrix contains at least one minor with order r and the minors with order greater than r is zero. The second method
12 min read
Unitary Matrix
Unitary Matrix: Unitary Matrices are defined as square matrices of complex numbers such that the product of the conjugate transpose of a unitary matrix, with the unitary matrix itself, gives an identity matrix. Matrices are defined as rectangular arrays in which numbers are arranged in rows and columns. Number of rows and columns determined the siz
5 min read
Zero Matrix
A zero matrix, or null matrix, is a matrix whose all elements are zeros. A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. A matrix is said to be an "m by n" matrix when it has "m" rows and "n" columns and is written as an "m ×
6 min read
Augmented Matrix
Augmented Matrix is a matrix that is formed when we combine the columns of two matrices and thus, form a new matrix. The new matrix so formed is called the Augmented Matrix. An Augmented Matrix is important to solve various types of problems in mathematics especially those which involve the use of equations. This article deals with the concept of a
10 min read
Matrix Multiplication Practice Questions
A matrix is a set of numbers arranged in rows and columns to form a rectangular array. Multiplying a matrix by another matrix is called "matrix multiplication". In this article, we will learn what matrix multiplication is. And practice some questions related to it. What is Matrix Multiplication?In linear algebra, a matrix is an arrangement of eleme
5 min read
Square Matrix
Square Matrix: A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. A square matrix is characterized by having the same number of rows as columns. It's referred to as an m x m matrix, indicating that it is a square matrix of order ?m. When two square matrices are either multiplied or added, the resultant matr
9 min read
Elements of Matrix
Elements of the Matrix are the components or entries of the Matrix. These elements could be any variables, numbers, a mix of variables and numbers, or any other kind of special characters as well. The number of elements of a matrix is equal to the product of the number of rows and columns present in a matrix. This article explores the concept of th
11 min read
Order of Matrix
Order of the matrix defines the number of rows and columns that a matrix has. In a matrix, data is arranged as an array of elements. This data is arranged in rows and columns, and the number of rows and columns any matrix has defines the Order of the matrix. Suppose any matrix has 5 rows and 3 columns then the order of the matrix is 5×3. In this ar
9 min read
How to Find Rank of a 3x3 Matrix
Rank of a matrix is equal to the number of linear independent rows or columns in it. The rank of the matrix is always less than or equal to the order of the matrix. In this article we will explore how to find rank of 3×3 matrix in detail along with the basics of the rank of a matrix. Table of Content What is Rank of a Matrix?How to Find Rank of a 3
7 min read
Inverse of 2x2 Matrix with Examples
Inverse of 2×2 matrix is the matrix obtained by dividing the adjoint of the matrix by the determinant of the matrix. The two methods to find the inverse of 2×2 matrix is by using inverse formula and by using elementary operations. In this article, we will explore how to find the inverse of 2×2 matrix along with both the methods and basics of the in
6 min read
Hermitian Matrix
A rectangular array of numbers that are arranged in rows and columns is known as a "matrix." The size of a matrix can be determined by the number of rows and columns in it. If a matrix has "m" rows and "n" columns, then it is said to be an "m by n" matrix and is written as an "m × n" matrix. For example, a matrix with five rows and three columns is
8 min read
Article Tags :