ECE 151 Fundamentals of Electronic Instrumentation

Name

Judy Ann B. Vargas

Date Performed

LAB 4
October 21, 2015

AC VOLTAGE & MEASUREMENT

Procedure
Part A

1. You are given a set of resistors. By using multi-meter, measure the resistance value and record
the reading in Table 1. Calculate the percentage error for each measurement and compare to
actual value using color code.

Part B
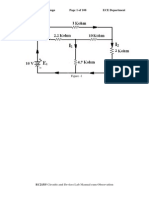
2. Construct a circuit as in Figure 1.

Figure 1

ECE 151 Fundamentals of Electronic Instrumentation

LAB 4

3. Apply AC input signal as indicate in Figure 1. Connect Channel 1 of oscilloscope to the input
signal and observe the output voltage Va and Vb using Channel 2. Measure and record the values
in Table 2.
4. Increase the amplitude of input signal of Channel 1 (refer Table 3 increment) and observe the
Voltage of Va and Vb and with your own word, make some discussion.

*Show all calculations in additional pages.

Data Table
Resistance Measurement
TABLE 1
Resistor

Measured

Color Code

% Error

R1

2.16 k

2.2 k

1.82%

R2

1.254 k

1.36 k

7.79%

R3

4.62 k

4.7 k

1.70%

R4

0.994 k

1 k

0.60%

Voltage Measurement

TABLE 2
Voltage

Measured Value

Calculated Value

% Error

Va

0.700 V

0.644 V

8.70%

Vb

0.580 V

0.530 V

9.43%

ECE 151 Fundamentals of Electronic Instrumentation

LAB 4

Increase Input Voltage

TABLE 3a: Voltage, Va

Measured Value

Calculated Value

% Error

1.44 V

1.287 V

11.89%

2.80 V

2.575 V

8.74%

15

5.20 V

4.828 V

7.71%

16

5.40 V

5.149 V

4.87%

TABLE 3b: Voltage, Vb

Measured Value

Calculated Value

% Error

1.20 V

1.060 V

13.20%

2.4 V

2.118 V

13.31%

15

4.40 V

3.973 V

10.75%

16

4.60 V

4.237 V

8.57%

Discussion/Analysis
As seen in the table above, we can see that as the amplitude is increased, the values of Va
and Vb also increases. Since the AC voltage changes values from time to time, unlike the DC
voltage which remains steady in time, it is difficult to point out the exact measurement. In the
experiment, we used the oscilloscope to be able to measure the voltages in the circuit. The value
of the voltage we chose to show is the peak-to-peak voltage or the total voltage from the positive
peak to the negative peak. Because the values changes, it is best to get the peak-to-peak values
because it mostly remains the same throughout the whole duration. Another value of the voltage
can be considered good to use is the root mean square or RMS voltage. Because of the changes

ECE 151 Fundamentals of Electronic Instrumentation

LAB 4

in values from the positive peak to the negative peak, it is really difficult to get the real effect of
the voltage. The RMS value is the effective value of the varying voltage. Therefore, this value is
somewhat the equivalent value if we measure it in DC. The peak-to-peak and RMS value of the
voltage is related as seen in the formula:
= 1.4

Calculations
Percentage Error for R1
% =

| |
|2.2 2.16 |
100 =
100 = 1.82%

2.2

Percentage Error for R2

| |
|1.36 1.254 |
100 =
100 = 7.79%

1.36

Percentage Error for R3

| |
|4.7 4.62 |
100 =
100 = 1.70%

4.7

Percentage Error for R4

| |
|1 0.994 |
100 =
100 = 0.60%

1

ECE 151 Fundamentals of Electronic Instrumentation

LAB 4

By KVL at Loop 1:
+ 1 1 + 2 (1 2 ) = 0
1 (1 + 2 ) 2 2 =
1 (3.414 ) 2 (1.254 ) =
1 =

+ 2 (1.254 )
3.414

(1)

By KVL at Loop 2:.6

(2)

= 1.254 (1 2 ) (3)
= 2 (4.62 ) (4)
Substituting (1) to (2)

2 (1.254 )
(
) (1.254 ) (
) (1.254 ) + 2 (6.868 ) = 0
3.414
3.414

2 (1.254 )
(
) (1.254 ) + 2 (6.868 ) = (
) (1.254 )
3.414
3.414
6.407 (2 ) =

209

569

2 = 5.733105

(5)

When Vpp = 2V, using equations (1) and (5) to get the currents and (3) and (4) for the voltage:
2 = 5.733105
2 = 5.733105 (2)
2 = 1.147104

ECE 151 Fundamentals of Electronic Instrumentation

LAB 4

+ 2 (1.254 )
3.414

2 + 1.147104 (1.254 )
3.414
1 = 6.279104

= 1.254 (1 2 )
= 1.254 (6.279104 1.147104 )
= 0.644

= 2 (4.62 )
= (1.147104 )(4.62 )
= 0.530

% =

| |
|0.644 0.700|
100 =
100 = 8.70%

0.644

% =

| |
|0.530 0.580|
100 =
100 = 9.43%

0.530

When Vpp = 4V, using equations (1) and (5) to get the currents and (3) and (4) for the voltage:
2 = 5.733105
2 = 5.733105 (4)
2 = 2.293104

1 =
1 =

+ 2 (1.254 )
3.414

4 + 2.293104 (1.254 )
3.414

ECE 151 Fundamentals of Electronic Instrumentation

LAB 4

1 = 1.256103

= 1.254 (1 2 )
= 1.254 (1.256103 2.293104 )
= 1.287

= 2 (4.62 )
= (2.293104 )(4.62 )
= 1.060

% =

| |
|1.287 1.44|
100 =
100 = 11.89%

1.287

% =

| |
|1.060 1.20|
100 =
100 = 13.20%

1.060

When Vpp = 8V, using equations (1) and (5) to get the currents and (3) and (4) for the voltage:
2 = 5.733105
2 = 5.733105 (8)
2 = 4.586104

1 =

+ 2 (1.254 )
3.414

8 + 4.586104 (1.254 )
1 =
3.414
1 = 2.512103

= 1.254 (1 2 )

ECE 151 Fundamentals of Electronic Instrumentation

LAB 4

= 1.254 (2.512103 4.586104 )

= 2 (4.62 )
= (4.586104 )(4.62 )
= 2.118

% =

| |
|2.575 2.80|
100 =
100 = 8.74%

2.575

% =

| |
|2.118 2.40|
100 =
100 = 13.31%

2.118

When Vpp = 15V, using equations (1) and (5) to get the currents and (3) and (4) for the voltage:
2 = 5.733105
2 = 5.733105 (15)
2 = 8.599104

1 =
1 =

+ 2 (1.254 )
3.414

15 + 8.599104 (1.254 )
3.414
1 = 4.710103

= 1.254 (1 2 )
= 1.254 (4.710103 8.599104 )
= 4.828

ECE 151 Fundamentals of Electronic Instrumentation

LAB 4

= 2 (4.62 )
= (8.599104 )(4.62 )
= 3.973

% =

| |
|4.828 5.20|
100 =
100 = 7.71%

4.828

% =

| |
|3.973 4.40|
100 =
100 = 10.75%

3.973

When Vpp = 16V, using equations (1) and (5) to get the currents and (3) and (4) for the voltage:
2 = 5.733105
2 = 5.733105 (16)
2 = 9.172104

1 =
1 =

+ 2 (1.254 )
3.414

16 + 9.172104 (1.254 )
3.414
1 = 5.023103

= 1.254 (1 2 )
= 1.254 (5.023103 9.172104 )
= 5.149

= 2 (4.62 )
= (9.172104 )(4.62 )
= 4.237

ECE 151 Fundamentals of Electronic Instrumentation

% =

| |
|5.149 5.40|
100 =
100 = 4.87%

5.149

% =

| |
|4.237 4.60|
100 =
100 = 8.57%

4.237

10

LAB 4