Assignment 6
Uploaded by
altoprimeAssignment 6
Uploaded by
altoprime( )
1. Identify which of these functions has a complex CTFS c g k for which 1) Re c g k = 0 for all k,
( )
or 2) Im c g k = 0 for all k, or 3) neither of these conditions applies.
(a) g ( t ) = 18cos ( 200p t ) + 22cos ( 240p t )
(b) g ( t ) = -4sin (10p t ) sin ( 2000p t )
t 1
(c) g t tri 10 t
4
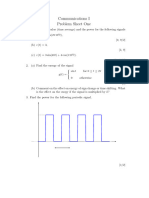
2. A system is excited by a signal x ( t ) = 4 rect ( t / 2 ) and its response is
( ) ( )
y ( t ) = 10 1- e-(t+1) u ( t +1) - 1- e-(t-1) u ( t -1) .
What is its impulse response?
j2p f
3. A signal x ( t ) has a CTFT X ( f ) = .
3 + jf /10
(a) What is the total net area under the signal x ( t ) ?
t
(b) Let y ( t ) be the integral of x ( t ) , y t x d . What is the total net area under
y(t ) ?
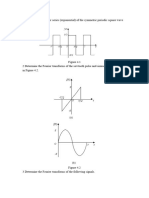
4. Find the numerical values of the literal constants in the following CTFT pairs.
(a)
(b)
(c)
(Hint: Use the definition of the continuous-time periodic impulse and
continuous-time impulse properties.)
(d)
5. An LTI continuous-time system is described by the differential equation 2 y ( t ) + 5y ( t ) = x ( t ).
Which is the correct description of this systems frequency response?
(a) The system attenuates low frequencies more than high frequencies.
(b) The system attenuates high frequencies more than low frequencies.
