Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
36 views

Tutorial 1

Uploaded by

Raj Gupta
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
36 views

Tutorial 1

Uploaded by

Raj Gupta
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 2

Tutorial - 1

ECC201: Fundamental of Communication Systems

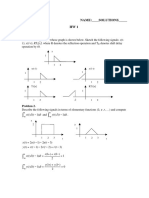
1. For the continuous-time signals shown below, sketch and label carefully the following signals respec-
tively:
(a) x (4 − 2t )
(b) x (3t + 1)

Figure 1: 1

2. Determine whether the following signals are periodic or not. If periodic, find the fundamental period.
(a) x (t) = 2 cos(10t + 1) − sin(4t − 1)
(b) x (t) = sin2 (t)
(c) x (t) = sin (2t) + cos (3πt)

3. Determine the value of E∞ and P∞ for each of the following signals:


(a) x1 (t) = e−2t u(t)
(b) x (t) = 2 sin (3πt) + 3 cos (3πt + π/3)
(c) x1 (t) = e− a|t| for a > 0

4. Consider the continuous-time signal:

x ( t ) = δ ( t + 2) − δ ( t − 2)

Calculate the value of E∞ for the signal:


Z t
y(t) = x (τ )dτ
−∞
5. Determine which of these properties hold and which do not hold for each of the following continuous-
time systems. Justify your answers. In each example, y(t) denotes the system output and x (t) is the
system input. In particular, a system may or may not be

1. Memoryless
2. Time invariant
3. Linear
4. Causal
5. Stable
R 2t
(a) y(t) = −∞ x (τ )dτ
(
0, x (t) < 0
(b) y(t) =
x ( t ) + x ( t − 2), x (t) ≥ 0
dx (t)
(c) y(t) = dt

6. Determine and sketch the convolution of the following two signals:



 t + 1, 0 ≤ t ≤ 1,

x (t) = 2 − t, 1 < t ≤ 2,

0, elsewhere

h(t) = δ(t + 2) + 2δ(t + 1).

7. (a) Consider an LTI system with input and output related through the equation

Rt
y(t) = −∞ e−(t−τ ) x (τ − 2)dτ.
What is the impulse response h(t) for this system?
(b) Determine the response of the system when the input x(t) is as shown in Figure 2.

Figure 2: 7(b)

Page 2

You might also like