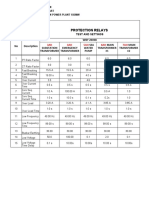
Design Differentiator Amplifier
Uploaded by
hareesh.makesuDesign Differentiator Amplifier
Uploaded by
hareesh.makesuHashemite University Department of Electrical and computer Engineering Electronics 2 Lab Final Project
Design Differentiator Amplifier
Using OrCAD PSpice 15.7
In this Project we achieve the differentiator Amplifier with given specifications, firstly theoretically and secondly simulation and implementation using PSpice 15.7.
Achieved by:
Abdul Karem Al sbeeh Ahmad Hussan Omar
Supervised By:
Dr: Osama Oquili
DESIGN DIFFERENTIATOR AMPLIFIER
Page 2
Theoretical Background
Chapter I
OP-Amp
An operational amplifier (op-amp) is a linear integrated circuit that incorporates a DC-coupled, high-gain differential amplifier and other circuitry that give it specific characteristics. The ideal op-amp has certain unattainable specifications, but hundreds of types of operational amplifiers are available, which vary in specific ways from the ideal op-amp. Important specifications include very large open-loop gain, high input impedance, and low output impedance. There are other specifications for op-amp that are important in certain applications. These specifications can be divided into two categories: DC parameters and AC parameters. DC parameters include input bias current, input offset current and input offset voltage. Input bias current ( I Bias ) is the average of the input currents required at each input terminal of the op-amp. Input offset current ( I OS ) is the absolute value of the difference between the DC bias currents.
IBias
I B1 2
I B2
(1)
Ios
give zero output voltage.
IB1 IB2
(2)
Input offset voltage ( VIO ) is the amount of voltage that must be applied between the input terminals of an op-amp to
Since the input stage of all op-amps is a differential amplifier, there are two inputs marked with the symbols (+) and (-). These symbols refer to the phase of the output signal compared to the input signal and should be read as non-inverting (+) and inverting (-) rather than plus or minus. If the non-inverting input is more positive than the inverting input, the output will be positive. If the inverting input is more positive, then the output will be negative. The symbol for an op-amp is shown in Figure 1(a). Figure 1(b) shows a typical 8-pin dual-in-package (DIP) with an identifier for pin 1. And Figure 2 shows the pin diagram for LM 741 op-amp.
Fig.1: (a) The Symbol for an Op-Amp
(b) Typical 8-pin DIP Op-Amp
DESIGN DIFFERENTIATOR AMPLIFIER
Page 3
Differentiator Amplifier
A differentiator circuit produces an output that is proportional to the derivative or rate of change of the input voltage over time. Differentiator circuit can be constructed as shown using an operational amplifier, a resistor, and a capacitor. Unlike an ideal integrator circuit where the slightest DC offset in the input eventually drives the output into saturation, for the differentiator we need not be concerned about a DC offset in the input since the derivative of a constant is always zero. For this circuit, it can be shown that:
Vout
RC
dVin dt
Fig.2: Differentiator Circuit
Since the output voltage of a differentiated is proportional to the input frequency, high frequency signals (such as electrical noise) may saturate or cutoff the amplifier. For this reason: a resistor is placed in series with the capacitor in the input as shown in Figure 5. This establishes high frequency limit beyond which differentiation no longer occurs:
g%
1 2SR in Cin
To achieve greater attenuation at higher frequencies (or prevent oscillation), a feedback capacitor is added in parallel with the feedback resistor. This establishes another break frequency that can be calculated as in the integrator. Fig.3: Stable Differentiator Circuit
DESIGN DIFFERENTIATOR AMPLIFIER
Page 4
Frequency Response
The frequency response of an amplifier is the variation in the output as the frequency is varied. The analysis of the frequency response of an amplifier can be considered in three frequency ranges: the low-, mid-, and high-frequency regions. In the low-frequency region the capacitors used for DC isolation (AC coupling) and bypass operation affect the lower cutoff (lower 3-dB) frequency. In the mid- frequency range only resistive elements affect the gain, the gain remaining constant. In the high-frequency region of operation, stray wiring capacitances and device inter-terminal capacitances will determine the circuit's upper cutoff frequency.
Practical Differentiator Amplifier
The ideal differentiator is inherently unstable in practice due to the presence of some high frequency noise in every electronic system. An ideal differentiator would amplify this small noise. For instance, if vnoise = Asin(wt) is differentiated, the output would be vout = Awcos(wt). Even if A = 1mV, when w = 2p(10MHz) vout would have an amplitude of 63V! To circumvent this problem, it is traditional to include a series resistor at the input and a parallel capacitor across the feedback resistor as shown in figure 2, converting the differentiator to an integrator at high frequencies for filtering.
DESIGN DIFFERENTIATOR AMPLIFIER
Page 5
Theoretical Design calculations
Chapter II
Calculated the cutoff frequency
Question: Design a practical differentiator with 2 kHz cutoff frequency, the gain at 10 Hz should be 0.1. = 1 2
Let me say that Rin = 3 k, then = 1 = 26.526 2
Av = 0.1 at 10 Hz =
Taken the Transform of differentiation by 2f
0.1 = 2 (10) Rfb (26.526 n) Rfb = 59.996 k
The Relation between input and output
To draw the Relation between the input and the output fig.4, we taken 10 values of input and calculate the output. Table 1: output voltage at different input Frequency 1 kHz 1 kHz 1 kHz 1 kHz 1 kHz 1 kHz 1 kHz 1 kHz 1 kHz 1 kHz
Input Voltage (volt) 0 0.499 0.99 1.499 1.989 2.499 2.989 3.499 3.989 4.499
Output Voltage (volt) 0 0.495 0.989 1.484 1.978 2.473 2.967 3.462 3.957 4.451
DESIGN DIFFERENTIATOR AMPLIFIER
Page 6
VIN = Am Sin (2 f t) where f = 1 kHz VOut = Am (2 f) RC Cos (2 f t)
Input Output Relationship at constant frequency
6 5 Vout (Volt) 4 3 2 1 0 0 1 2 3 Vin (volt) 4 5 6
Fig.4: the Relationship between the input and output From the same expression VOut = Am (2 f) RC Cos (2 f t) and from the frequency Response that see later, the differentiator begins differentiates the input at 10 Hz and to value of output not exceed 20 V, then the differentiator work as inverting.
The Frequency Response
We apply the same expression to find the output voltage by: VOut = Am (2 f) RC Cos (2 f t) Table 2: the output voltage at different frequency Frequency (Hz) 10 50 100 150 200 246 294 342 390 438 486 534
Input Voltage (volt) 1 1 1 1 1 1 1 1 1 1 1 1
Output Voltage (volt) 0.100013 0.500065 1.00013 1.500194 2.000259 2.460319 2.940381 3.420443 3.900506 4.380568 4.86063 5.340692
DESIGN DIFFERENTIATOR AMPLIFIER
Page 7
582 630 678 726 774 822 870 918 966
1 1 1 1 1 1 1 1 1
5.820754 6.300817 6.780879 7.260941 7.741003 8.221066 8.701128 9.18119 9.661252
Output Voltage at deffrent frequency
25 20 Output (Volt) 15 10 5 0 0 1000 2000 3000 Frequency (Hz) 4000 5000 6000
Fig.5: output voltage with respect to different frequency
DESIGN DIFFERENTIATOR AMPLIFIER
Page 8
Design and Simulation using OrCAD 15.7
Chapter III
We draw the differentiator amplifier without feedback capacitor as you can see below:
Figure 6: Differentiator without capacitor as feed back
And then we draw the differentiator amplifier with feedback capacitor, to calculate the upper cutoff frequency as you can see below:
Figure 7: Differentiator with capacitor as feed back
DESIGN DIFFERENTIATOR AMPLIFIER
Page 9
From the two pages coming later, each one has graph of frequency response the first one ha sfrequency response without feedback capcitor and the second one with feedback capacitor. We must calculate the value of capacitor that prevent the high frequency as this: The High frequency begins at 20 V equal 20.045 kHz then:
1 2
: where RC the parallel companation at feedback.
C = 0.13 nF We can can see in the second graph the lower and upper cutoff frequency.
Discuss the Result:
1. We can see from first graph of frequency Response, that the diffrentiator begins work at 10 Hz to value at output voltage equal 20 V 20.045 KHz. 2. The maximum value of ouput voltage in fig.6 is more garater than in fig.7 because the losses in filter circuit in feed back. 3. There is region in curve in frequency Response is a linear region, where circuit work as a good diffrentiator.
DESIGN DIFFERENTIATOR AMPLIFIER
Page 10
conclusions:
In this project we know that the practical diffrentiator is different than ideal. And when you want to design the diffrentiator you must taken many things in your consideration, such as upper and lower cutoff frequency,and the band width of the amplifier. To prevent a high frequency problem in this diffrentiator we use the low pass filter, you can see that in feedback in fig.7. The relationship between input voltage and output voltage is linear in linear Region. The best thing in this project we know how we can use the other software" PSpice" to build schematic and simulation it.
Refrences:
1. Electronic circuit analysis and Design, by Donald A Neamen. 2. OrCad 15.7
You might also like
- Op-Amps and Linear Integrated Circuits, Fourth Edition by Gayakwad, Ramakant A19% (16)Op-Amps and Linear Integrated Circuits, Fourth Edition by Gayakwad, Ramakant A1 page
- Design of Electrical Circuits using Engineering Software ToolsFrom EverandDesign of Electrical Circuits using Engineering Software ToolsNo ratings yet
- Op-Amp Comparator and The Op-Amp Comparator CircuitNo ratings yetOp-Amp Comparator and The Op-Amp Comparator Circuit18 pages
- Differential Amplifier and CMRR SignificanceNo ratings yetDifferential Amplifier and CMRR Significance32 pages
- Network Filters and Transmission Line: ContentNo ratings yetNetwork Filters and Transmission Line: Content36 pages
- Difference Between Photodiode & Phototransistor: Comparison ChartNo ratings yetDifference Between Photodiode & Phototransistor: Comparison Chart5 pages
- A Car Parking Guard Circuit Using InfrarNo ratings yetA Car Parking Guard Circuit Using Infrar12 pages
- Design of Low-Power High-Gain Operational Amplifier For Bio-Medical ApplicationsNo ratings yetDesign of Low-Power High-Gain Operational Amplifier For Bio-Medical Applications6 pages
- Download Full Operational Amplifiers and Linear Integrated Circuits 6th Edition Robert F. Coughlin PDF All Chapters100% (17)Download Full Operational Amplifiers and Linear Integrated Circuits 6th Edition Robert F. Coughlin PDF All Chapters71 pages
- Iot Based Vehicle Theft Detection Using Raspberry Pi: Mrs. S NandiniNo ratings yetIot Based Vehicle Theft Detection Using Raspberry Pi: Mrs. S Nandini15 pages
- Experiment Kit For Study of Sample and Hold Circuit: User ManualNo ratings yetExperiment Kit For Study of Sample and Hold Circuit: User Manual24 pages
- Unit-III-Signal Generators & Wave Analyzers PDF100% (1)Unit-III-Signal Generators & Wave Analyzers PDF33 pages
- The Unijunction Transistor (UJT) - ThyristorsNo ratings yetThe Unijunction Transistor (UJT) - Thyristors6 pages
- Experiment No 9 Single Stage RC Coupled Common Emitter AmplifierNo ratings yetExperiment No 9 Single Stage RC Coupled Common Emitter Amplifier6 pages
- Unit-I - Feedback Amplifiers Two Marks Question & AnswerNo ratings yetUnit-I - Feedback Amplifiers Two Marks Question & Answer4 pages
- Simulation of Some Power System, Control System and Power Electronics Case Studies Using Matlab and PowerWorld SimulatorFrom EverandSimulation of Some Power System, Control System and Power Electronics Case Studies Using Matlab and PowerWorld SimulatorNo ratings yet
- Differentiator and Integrator (Aartimam)No ratings yetDifferentiator and Integrator (Aartimam)34 pages
- Differentiator Op-Amp-Report-ElectronicsNo ratings yetDifferentiator Op-Amp-Report-Electronics10 pages
- AVTC Model Based Design Curriculum Development ProjectNo ratings yetAVTC Model Based Design Curriculum Development Project13 pages
- A.C Voltage Controllers With R and RL LoadsNo ratings yetA.C Voltage Controllers With R and RL Loads1 page
- Muffakham Jah College of Engineering and Technology Electrical Engineering DepartmentNo ratings yetMuffakham Jah College of Engineering and Technology Electrical Engineering Department3 pages
- Overview of Speech Enhancement: 3.1 PsychoacousticsNo ratings yetOverview of Speech Enhancement: 3.1 Psychoacoustics19 pages
- Bcd-To-Seven-Segment Decoders/Drivers: No: 22, Group: E&I, Batch: 2013-15No ratings yetBcd-To-Seven-Segment Decoders/Drivers: No: 22, Group: E&I, Batch: 2013-154 pages
- Crystal System: Crystallography Space Groups Lattices Point Groups CrystalsNo ratings yetCrystal System: Crystallography Space Groups Lattices Point Groups Crystals7 pages
- Speech Recognantion and Verification System To Identifing The Isolated Words Using MatlabNo ratings yetSpeech Recognantion and Verification System To Identifing The Isolated Words Using Matlab1 page
- True Zero-Speed, High Accuracy Gear Tooth Sensor IC: ATS667LSGNo ratings yetTrue Zero-Speed, High Accuracy Gear Tooth Sensor IC: ATS667LSG14 pages
- CYCLE-2:Experiment 1 Steady-State Performance of A 3-Phase Induction MotorNo ratings yetCYCLE-2:Experiment 1 Steady-State Performance of A 3-Phase Induction Motor32 pages
- Full Professor Nguyen Duc Hoa,: Brief Research Plan During My VisitNo ratings yetFull Professor Nguyen Duc Hoa,: Brief Research Plan During My Visit3 pages
- Condensed Intro To Tesla Transformers PDFNo ratings yetCondensed Intro To Tesla Transformers PDF56 pages
- BES 516-300-S266-S4 Order Code: BHS0034: Inductive SensorNo ratings yetBES 516-300-S266-S4 Order Code: BHS0034: Inductive Sensor2 pages
- GitHub - Ahmibr - ELC325-Digital-Communication - Digital Communications Matlab Simulink Project PDFNo ratings yetGitHub - Ahmibr - ELC325-Digital-Communication - Digital Communications Matlab Simulink Project PDF18 pages
- Op-Amps and Linear Integrated Circuits, Fourth Edition by Gayakwad, Ramakant AOp-Amps and Linear Integrated Circuits, Fourth Edition by Gayakwad, Ramakant A
- Design of Electrical Circuits using Engineering Software ToolsFrom EverandDesign of Electrical Circuits using Engineering Software Tools
- Op-Amp Comparator and The Op-Amp Comparator CircuitOp-Amp Comparator and The Op-Amp Comparator Circuit
- Difference Between Photodiode & Phototransistor: Comparison ChartDifference Between Photodiode & Phototransistor: Comparison Chart
- Design of Low-Power High-Gain Operational Amplifier For Bio-Medical ApplicationsDesign of Low-Power High-Gain Operational Amplifier For Bio-Medical Applications
- Download Full Operational Amplifiers and Linear Integrated Circuits 6th Edition Robert F. Coughlin PDF All ChaptersDownload Full Operational Amplifiers and Linear Integrated Circuits 6th Edition Robert F. Coughlin PDF All Chapters
- Iot Based Vehicle Theft Detection Using Raspberry Pi: Mrs. S NandiniIot Based Vehicle Theft Detection Using Raspberry Pi: Mrs. S Nandini
- Experiment Kit For Study of Sample and Hold Circuit: User ManualExperiment Kit For Study of Sample and Hold Circuit: User Manual
- Experiment No 9 Single Stage RC Coupled Common Emitter AmplifierExperiment No 9 Single Stage RC Coupled Common Emitter Amplifier
- Unit-I - Feedback Amplifiers Two Marks Question & AnswerUnit-I - Feedback Amplifiers Two Marks Question & Answer
- Simulation of Some Power System, Control System and Power Electronics Case Studies Using Matlab and PowerWorld SimulatorFrom EverandSimulation of Some Power System, Control System and Power Electronics Case Studies Using Matlab and PowerWorld Simulator
- Computer Aided Design of Electrical MachinesFrom EverandComputer Aided Design of Electrical Machines
- AVTC Model Based Design Curriculum Development ProjectAVTC Model Based Design Curriculum Development Project
- Muffakham Jah College of Engineering and Technology Electrical Engineering DepartmentMuffakham Jah College of Engineering and Technology Electrical Engineering Department
- Overview of Speech Enhancement: 3.1 PsychoacousticsOverview of Speech Enhancement: 3.1 Psychoacoustics
- Bcd-To-Seven-Segment Decoders/Drivers: No: 22, Group: E&I, Batch: 2013-15Bcd-To-Seven-Segment Decoders/Drivers: No: 22, Group: E&I, Batch: 2013-15
- Crystal System: Crystallography Space Groups Lattices Point Groups CrystalsCrystal System: Crystallography Space Groups Lattices Point Groups Crystals
- Speech Recognantion and Verification System To Identifing The Isolated Words Using MatlabSpeech Recognantion and Verification System To Identifing The Isolated Words Using Matlab
- True Zero-Speed, High Accuracy Gear Tooth Sensor IC: ATS667LSGTrue Zero-Speed, High Accuracy Gear Tooth Sensor IC: ATS667LSG
- CYCLE-2:Experiment 1 Steady-State Performance of A 3-Phase Induction MotorCYCLE-2:Experiment 1 Steady-State Performance of A 3-Phase Induction Motor
- Full Professor Nguyen Duc Hoa,: Brief Research Plan During My VisitFull Professor Nguyen Duc Hoa,: Brief Research Plan During My Visit
- BES 516-300-S266-S4 Order Code: BHS0034: Inductive SensorBES 516-300-S266-S4 Order Code: BHS0034: Inductive Sensor
- GitHub - Ahmibr - ELC325-Digital-Communication - Digital Communications Matlab Simulink Project PDFGitHub - Ahmibr - ELC325-Digital-Communication - Digital Communications Matlab Simulink Project PDF